Bassey UN and Oyadare OO
This paper extends the Helgason-Schiffman formula for the H-function on a semisimple Lie group of real rank one to cover a semisimple Lie group G of arbitrary real rank. A set of analytic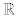 
-valued cocycles are deduced for certain real rank one subgroups of G. This allows a formula for the c-function on G to be worked out as an integral of a product of their resolutions on the summands in a direct-sum decomposition of the maximal abelian subspace of the Lie algebra g of G. Results about the principal series of representations of the real rank one subgroups are also obtained, among other things.
Share this article
