Physical Mathematics

On the Identity-Power Graphs of Finite Groups

Abstract

Abor Isa Garba*, MS Magami and O Ejima

Let G be a finite group, the associated identity-power graph Γ (G) is a graph whose vertices V (Γ(G)) are precisely the elements of G and two distinct vertices x,y create the oriented edge (x, y) if and only if xy=e or yx=e (where e is the identity of the group G) and either x=yn or y=xn for some n € N. We investigate some algebraic properties and combinatorial structures of the identity-power graph Γ (G) and show that the graph Γ(G) of a finite group G, is never complete. We also show that if every element x in a finite group G has a unique inverse y € G, and then the identity-power graph of G is acyclic. Furthermore, we show that the size of the identity-power graph Γ (M) of a permutation group M is given by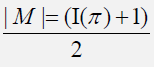. Where π € M and I (π) is the set of involutions in M.