Journal of Generalized Lie Theory and Applications

A three dimensional Sklyanin is the quadratic algebra over a field 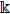with 3 generators x; y; z given by 3 relations xy - ayx - szz = 0, yz - azy - sxx = 0 and zx - axz - syy = 0, where a,s ∈ 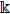. A generalized Sklyanin algebra is the algebra given by relations xy - a₁yx - s₁zz = 0, yz - a₂zy - s₂xx = 0 and zx - a₃xz - s₃yy = 0, where a_i, s_i∈ 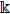. In this paper we announce the following results; the complete proofs will appear elsewhere. We determine explicitly the parameters for which these algebras has the same Hilbert series as the algebra of commutative polynomials in 3 indeterminates as well as when these algebras are Koszul and PBW, using constructive combinatorial methods. These provide new direct proofs of results established first by Artin, Tate, and Van Den Bergh.

Symmetry group of Lie algebras and superalgebras constructed from (ϵ,δ) Freudenthal-Kantor triple systems has been studied. Also, the definition and examples of hermitian triple systems is introduced in this note.

A corrected list of the Mubarakzyanov algebras, that is, six-dimensional indecomposable solvable Lie algebras for which the nilradical is five-dimensional, is presented. For each class of algebra a matrix representation and a system of vector fields representation is given. As a consequence it follows that the dimension of the minimal matrix representation of any six-dimensional Lie algebra is at most six.

In this paper we introduce color Hom-Poisson algebras and show that every color Hom-associative algebra has a non-commutative Hom-Poisson algebra structure in which the Hom-Poisson bracket is the commutator bracket. Then we show that color Poisson algebras (respectively morphism of color Poisson algebras) turn to color Hom-Poisson algebras (respectively morphism of Color Hom-Poisson algebras) by twisting the color Poisson structure. Next we prove that modules over color Hom–associative algebras A extend to modules over the color Hom-Lie algebras L(A), where L(A) is the color Hom-Lie algebra associated to the color Hom-associative algebra A. Moreover, by twisting a color Hom-Poisson module structure map by a color Hom-Poisson algebra endomorphism, we get another one.

In this paper we discuss the normal ordering procedure of the q-deformed generalized Heisenberg algebra. We also obtain the coherent state for some types of characteristic functions.