Research - (2024) Volume 15, Issue 5
Received: 22-Jan-2020, Manuscript No. JFR-20-002-PreQc-20;
Editor assigned: 11-Feb-2020, Pre QC No. JFR-20-002-PreQc-20;
Reviewed: 15-Feb-2020, QC No. JFR-20-002-PreQc-20;
Revised: 25-Jan-2021, Manuscript No. JFR-20-002-PreQc-20(A);
Published:
16-Mar-2021
, DOI: 10.37421/2157-7145.2024.15.002
, QI Number: JFR-20-002-PreQc-20
Citation: Rajagopal, Saranya, Mohan Vasudev and Lakshmanan Rajendran."A Mathematical Approach on Glucose-Insulin Supervisory Classification with the Impact of Non-Stationary Diffusion using Homotopy Perturbation Method ." J Forensic Res 13(2021): 002.
Copyright: �?�© 2021 Saranya R, et al. This is an open-access article distributed under the terms of the creative commons attribution license which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
Sources of funding : None
Diabetes mellitus remains a clutch of metabolic illnesses using inflated plasma glucose absorption as the foremost indication. It will be affected by a comparative or an aggregate deficiency of insulin which is created through the β-cells. Current trial outcomes designated the significance of the β-cell sequence intended for the enlargement of diabetes. This paper influences the analytical and numerical solutions of the system of nonlinear differential equations based on non-stationary diffusion containing a nonlinear term related to the kinetics of the enzymatic reaction. The Homotopy Perturbation Method (HPM) is expended to discover the analytical expressions of the glucose, Insulin, and β-cell mass respectively. The paradigm and its improvement are presented as well as the aforementioned mathematical investigation with thirteen parameters. Comparative analysis of analytical approximation and numerical simulations are also presented.
Mathematical model • Glucose • Insulin • Non-linear equations
Across the global, diabetes distresses around 37crores individuals and it is the key reason for almost fifty lakhs demises [1]. Diabetes mellitus is a cluster of metabolic ailments with augmented lifeblood glucose absorption by way of foremost indication. Shortage of insulin leads to Diabetes that is created by means of the β-cells in the pancreatic isles of Langerhans. Insulin, a hormone which raises the absorptivity of the cubicle tissue for glucose particles and controls in this fashion the acceptance of glucose in cells. Boutayeb et.al deliberated the consequence of genetic tendency to diabetes on changing aspects of β-cells, glucose in addition to insulin. Insulin excretion is one and only supreme typical structures of β-cell composition [2]. Consequently, a nonexistence of insulin indicates to a letdown of directive of glucose homeostasis and grounds the core sign of diabetes mellitus, a persevering amplified concentration of blood sugar that is hyperglycemia. The additional communal type 2 diabetes is categorized by insulin confrontation of the mark chambers whereas Type 1 diabetes is an autoimmune illness where the virus abolishes the insulin making β-cells. Han et.al designated possessions of the breach connection pairing among β-cells on the underlying forces of insulin emission. The inferences of paracrine exchanges in the middle of such isle chambers as α-, β- and β-cells are conferred and incorporated the properties of glycolysis and mitochondrial glucose uptake on the switch of insulin exudation. Glucose- insulin directive is concerned and the variation of β-cells is inadequate to recompense for this dysfunction in both states. Glucose is the vitality basis intended for the cells and is mostly acquired by celluloses in food. Raise of plasma glucose absorption is perceived by the β-cells. It grounds them to discharge deposited insulin particles and to yield fresh insulin [3]. Gallenberger et al described the relationship of glucose, insulin, and β-cell phase with a scheme of ordinary differential equations and investigated the stable positions of the model and their solidity.
The Beta Cells are liable for the release of insulin in reaction to raised plasma glucose stages, and the breakdown of these cells is a foremost provider to the growth of diabetes [4]. M. G. Pedersen explained the incidence of numerous arrangements of stuffed and calcium alternations and estimated in vivo beta-cell operational. Ha et.al suggested the prototypical that is further a layer of measured adverse response to the standard insulin-glucose circle in the system of a relaxed, glucose-reliant on natal and decease law leading β-cell form. The model enumerates the comparative assistances of insulin accomplishment and insulin discharge and a significance of an inception splitting the norm glycemic and diabetic conditions that motivates the realization of bariatric operation and acute caloric constraint in promptly retreating Type 2 Diabetes [5,6]. Unified the glucose insulin governing scheme and examined its varying traits as well as the association between the microscopic insulin evacuation contrivance on the cubicle level and the macroscopic glucose–insulin parameter tool at the whole-body level, in the occurrence of the interfaces amongst electrically joined β-cells. Several scientific representations projected for glucose parameter in the humanoid build, deliberated the effort and restraint in replicating actual procedures of glucose directive. EBM et.al outspreaded the effort that integrates an interval stays in the communication period of the glucose and insulin. The steadiness possessions were considered and determined the results using algebraic simulations. Sandhya and D. Kumar suggested a novel method to normalize the plasma glucose level of diabetes and simulated for measuring the effectiveness to yield the numerical solutions [7,8]. K. D. Shiang and F. Kandeel presented constraints assessment for a scheme of ordinary differential calculations through reducing the amount of adjusted residuals utility that enumerates the variance among speculative typical likelihoods and glucose tolerance test investigational annotations. The course of approximation was smeared using trepidation search and many shelling approaches. S. Singh and D. Kumar planned the consequence of bodily actions on glucose-insulin supervisory structure aimed at together non-diabetic individual and diabetic tolerant. Moreover, they determined that the glucose near declines by the result of corporeal accomplishments in everyday lifecycle repetitive of a diabetic category. R. Sweet and F. M. Matschinsky established a reckonable assessment that lucokinase panels the amount of glucose digestion and so the proportion of insulin exudation. Yasini et al established a novel methodology to control the lifeblood glucose level of type I diabetic tolerant underneath a concentrated insulin management. The closed-loop regulator system combined the proficient facts almost action by via fortification erudition concept to preserve the norm glycemic mediocre of 80 mg/dl and the usual form aimed at allowed plasma insulin deliberation in simple early state. The insulin transfer frequency is found off by using Q-learning system. Switch enactment was weighed in relations of the aforementioned knack to discard the outcome of suppertime trouble and to astound the inconsistency in the glucose-insulin underlying forces from tolerant to tolerant. Virtual reality was recycled to calculate the efficacy of the recommended performance and to demonstrate its dominance in governing hyperglycemia. Two theoretical model studies have examined coupled glucose and insulin dynamics. Topp et al introduced a precise model of β-cell form dynamics as a module of an attached archetypal of β-cell frame, insulin, and glucose subtleties. The regular performance of the classification is observed and examined the properties of a solitary flaw or an arrangement of weaknesses on the conduct of the complete process. Develop a mathematical model of β-cell mass, insulin and glucose dynamics. To our knowledge, no rigorous analytical solutions for non-steady state concentration glucose, insulin and β-cell mass have been reported. In this paper, we derived analytical expressions of concentration glucose, insulin and β-cell mass using homotopy perturbation method.
Mathematical formulation of the problem
Consider a mathematical model comprised of glucose level (G), insulin level (I) and β-cell mass (β). The model for glucose, insulin and cell mass dynamics are defined as follows :
Glucose Dynamics:
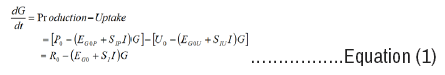
where G is the concentration of glucose in the blood (measured in mg dl-1), and t the time (days) P0 and U0 are the rates of glucose production and uptake at zero glucose (mg dl-1 d-1) EG0P and EG0U(d-1) are glucose effectiveness at zero insulin for production and uptake. SIP, SIU(μU-1 mld-1) are insulin sensitivity for production and uptake, and I represent blood insulin concentration (μUml-1). R0= P0-U0is the net rate of production at zero glucose, EG0=EG0P+EG0U is the total glucose effectiveness at zero insulin, and SI =SIP+SIU is the total insulin sensitivity.
Insulin Dynamics:
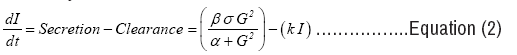
Numerical simulation
The importance of the accurate reference data and of the testing/validation of electrochemical modeling /simulation algorithms is recognized. The nonlinear reactions are also solved numerically by using Scilab program. To validate our analytical results, the numerical solutions are compared with our analytical results in Table 1. The close agreement between the analytical and simulation results, validates our analytical result. The maximum average error between analytical results and the simulation results for the concentration of glucose, insulin, β-cell mass are 0.44%, 2.83% and 2.71%, respectively.
| Time t (days) | Concentration of glucose G | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| when Gini | when G=250 mg dl | when G=500 mg dl | |||||||
| Simulation | Eq.(11) | % of Error deviation | Simulation | Eq.(11) | % of Error deviation | Simulation | Eq.(11) | % of Error deviation | |
| 0 | 000.19 | 000.19 | 0.00 | 250.00 | 250.00 | 0.00 | 500.00 | 500.00 | 0.00 |
| 0.25 | 188.30 | 188.90 | 0.00 | 355.10 | 360.20 | 1.41 | 531.50 | 531.48 | 0.00 |
| 0.5 | 310.50 | 310.50 | 0.00 | 427.30 | 430.90 | 0.83 | 551.70 | 551.68 | 0.00 |
| 0.75 | 396.80 | 396.20 | 0.15 | 479.80 | 480.70 | 0.18 | 565.90 | 565.90 | 0.00 |
| 1 | 462.30 | 460.60 | 0.36 | 519.20 | 518.30 | 0.17 | 576.60 | 576.60 | 0.00 |
| 1.25 | 505.50 | 501.90 | 0.71 | 544.00 | 542.40 | 0.29 | 583.50 | 583.50 | 0.00 |
| 1.5 | 540.00 | 538.50 | 0.27 | 563.00 | 560.50 | 0.44 | 588.70 | 588.70 | 0.00 |
| 1.75 | 563.80 | 554.10 | 1.72 | 577.70 | 572.10 | 0.97 | 592.00 | 592.00 | 0.00 |
| 2 | 580.20 | 566.70 | 2.32 | 594.00 | 580.40 | 2.34 | 594.40 | 594.38 | 0.00 |
| Average error % | 0.614 | Average error % | 0.731 | Average error % | 0.00 | ||||
Diabetes management is one of the most important issues in the field of human regulatory systems. It shows the difference between the glucose-insulin regulatory system, between a normal person and a diabetic person. In this paper, a mathematical model is developed for different values of Gini. Different graphs are obtained for glucose, insulin and β-cell mass concentration. The proposed model has successfully revealed the results for different possible scenarios. For example, the glucose concentration of a diabetic patient does not decline in time, which form an evidence that the person suffers from diabetes.
The total insulin sensitivity SI , net rate of production at zero glucose(R0 )initial concentration of insulin()iniIand initial concentration of glucose (Gini)lead to an increase in the concentration of glucose. It is found that the concentration increases when the parameter glucose effectiveness at zero insulin (EG0)decreases.
Differential sensitivity analysis of parameters
From the analysis it is inferred that, total glucose effectiveness at zero insulin (EG0 have more impact in the concentration of glucose. In contrast the parameter maximal rate of secrete insulin(σ), equilibrium constant for dissociation(α), clearance constant(k) and initial β-cell mass(β).
In this paper, the theory of glucose, insulin, and β-cells kinetics is described as a mathematical model. Approximate analytical solutions of non-linear reaction equations are presented using homotopy perturbation method. A simple, straight forward and a new method of estimating the glucose-insulin,β-cell mass are derived. The obtained analytical results will be useful to know the behavior of the reaction systems. The accuracy of the analytical solutions were shown to be very satisfactory when compared with numerical simulation data. The extension of this method with more modeling and simulation procedures to some of the nonlinear reaction-diffusion mechanism in glucose-insulin systems seems possible.
The authors declare no competing financial interest.
Journal of Forensic Research received 2328 citations as per Google Scholar report