Research Article - (2020) Volume 11, Issue 2
Received: 18-Apr-2020
Published:
12-May-2020
, DOI: 10.37421/2090-0902.2020.11.317
Citation: Ye, Fred Y. “A Mathematical Principle of Quantum Mechanism.†J Phys Math 11 (2020): 317 doi: 10.37421/JPM.2020.11.317
Copyright: © 2020 Fred Y Ye. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited
A mathematical cliff consists of scalar, vector and spinor, while scalar, vector and spinor are cliff components. It is found that the static exchange product of cliff components produces quantum, such as exchange multiplication of scalar and vector [X, Y]=XY–YX = â„Â/i, and that the complex dynamic distribution of i(z) as logarithm of negative numbers is just probability density, yielding quantum statistical mechanism. The mathematical principle reveals physical implications characterized by static “one cliff, one state” and dynamic “i(z) generates probability”, where the complex conjugation of the cliff indicates entangled one, resembling a concise mathematical principle of quantum mechanism. While the inner relations among scalars, vectors and spinors reveal local laws, the outer relations between cliffs describe global laws, leading to harmonic mathematical physics.
Cliff • Clifford algebra • Spinor • Quantum mechanism • Mathematical principle
Any physical progress is partly determined by mathematical innovation, as if calculus for classical mechanics and tensor method for relativity. In contemporary physics [1], both particle standard model based on quantum field theory and cosmological standard model based on general relativity followed modern mathematical methodologies, along the way through 17th century to 20th century.
A new way focuses on Clifford algebra and geometric calculus [2], which provided a new mathematical framework for processing physical issues, called as a mathematical language of 21st century [3,4]. With merging known mathematical elements, the Clifford algebra and its calculus analysis may integrate and unify mathematics and physics together [5].
In Clifford algebra, a compound number is called a cliff or a multi-vector Mk (k = 0, 1, 2, 3, 4), where Mk is a cliff of grade k, k=0 corresponds to scalar, k=1 to vector, k=2 to bivector, k=3 to trivector as pseudovector, and k=4 to pseudoscalar (closure to scalar). Mk is functional of space-time, on which any cliff or compound number may consist of three parts [6]: complex scalar z=M0+iM4, complex vector A=M1+iM3, and bivector B=M2. Now we write a cliff as
M = (z,A,B) (1)
where z is a complex scalar while A indicates a complex vector and B denotes a spinor, replacing bivector.
On the basis of above concepts, a new mathematical methodology can be set up for understanding quantum mechanism as well as mathematical physics.
Writing two cliffs M1 and M2
M1 = (z1, A1, B1) (2)
M2 = (z2, A2, B2) (3)
They construct a mathematical ring with two operators + (addition and subtraction) and * (multiplication and division), and there exists the third mathematical operation, i.e. calculus (differential and integral). The scalars, vectors and spinors are the components of cliffs.
While z, A and B abide by mathematical rules according to scalar, vector and spinor operations respectively, cliffs Mk will follow the Clifford algebraic rules, where the addition (and subtraction) happen in same cliffs when negative element exists
M1 + M2 = (z1 + z2, A1+ A2, B1 + B2) (4)
There are exchange law and combination law in addition (and subtraction)
M1 + M2 = M2 + M1 (5)
(M1 + M2) + M3 = M1 + ( M2 + M3 ) (6)
Multiplication (and division) can happen in same and different cliffs. However, exchange law and combination law do not generally exist here, where the multiplication is consisted of interior (dot) product and exterior (wedge) product as
M1 ∗ M2 = M1 ⋅ M2 + M1 ∧ M2 (7)
in which dot product did grade-reducing and wedge product did gradeincreasing . Generally, the algebra is a neither communicative nor associative system. If there is asymmetric communicative relation
M1 ∗ M2 = -M2 ∗ M1 (8)
the mathematical system is anti-communicative ring. The revised conjugation of M is denoted as M̅
M = (z,-A, B) (9)
and then any real variable x associates its conjugate x’ as
x ' = BxB (10)
The entanglement will happen between M and M̅, which is a basic phenomenon as there exists entangled quantum pair, visualized by right vortex particle and left vortex particle, as shown as Figure 1.
When an entangled particle is also an anti-particle of the particle, they construct Majorana particles.
Three Pauli matrices σk = (σ1, σ2, σ3) and unit matrix σ0 are applied as orthonormal basis
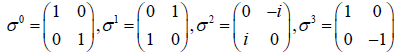 (11)
(11)
and they are extended as spinor basis on spinor indices K, L’, i.e. σ-type spinor matrices as
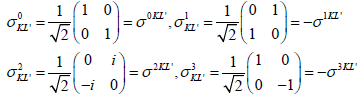 (12)
(12)
where K’ or L’ denotes complex conjugate of K or L.
Also, γμ (μ= 0,1,2,3) are applied as four Dirac matrices as four orthonormal basis in space-time
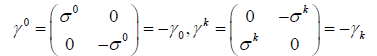 (13)
(13)
in which γ0 is time-like base, γk (k= 1,2,3) space-like bases, and their γ-type spinor matrices as
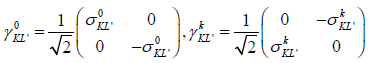 (14)
(14)
Spinors and tensors can be translated each other [7,8], where only difference is the purely formal one of replacing each tensor index by a pair of spinor indices. The spinors are more fundamental than tensors in the description of space-time structure and spins, as spinors can be used to describe particles with spins 1/2, 3/2, … in addition to those with spins 0, 1, 2.., whereas tensors can describe only the latter kind of spins. Therefore, we can replace tensors with spinors for theoretical perfection, but we can also keep tensors for computational convenience.
The world metric g as geometric metric also links spinor with tensor, as follows
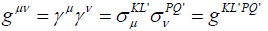 (15)
(15)
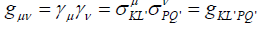 (16)
(16)
where space-time metric guv or guv is naturally generated, in which small Greek subscripts indicate tensor and capital Latin subscripts represent spinor, with traversing 0,1, 2, 3.
A spinor B has its complex conjugate B̅. While the label K’ is regarded as the complex conjugate of the label K, there exists
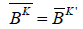 (17)
(17)
The raising and lowering spinor indices is similar to that of tensors in raising and lowering space-time indices as
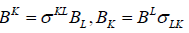 (18)
(18)
The scalar and vector partial differential operator gives normal calculus as
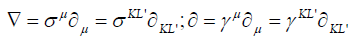 (19)
(19)
where operator ∇ acts on Clifford system Cl3 and operator ∂ acts on Cl1,3, and the Greek subscripts follow Einstein sum rule.
The two order derivatives can be introduced and defined as
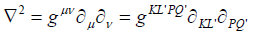 (20)
(20)
The spinor covariant derivative can be defined as
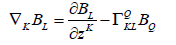 (21)
(21)
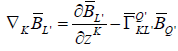 (22)
(22)
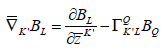 (23)
(23)
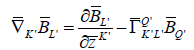 (24)
(24)
where all quantities Γ are spinor affine connections, on which curvature spinor is constructed as
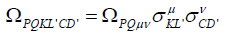 (25)
(25)
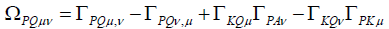 (26)
(26)
The operator of dual indices spinor derivative is defined as
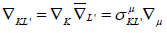 (27)
(27)
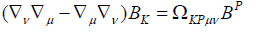 (28)
(28)
The differential process can also be viewed as a geometric calculus operator ∇ acting on functional linearly. A differential operation acting on a geometric functional F(M) is equivalent to the geometric product as
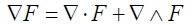 (29)
(29)
When S is a k-dimensional surface, if we interpret an element of directed area dS as a k-vector-valued measure on S and dA is a (k-1)-vector-valued measure on boundary ∂S, we get the generalized Stokes theorem between differential form ω=dA•F and its exterior derivative dω=dS•(▽∧F)
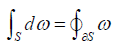 (30)
(30)
Above mathematical structure and calculus set up a new cornerstone towards unified physics.
A cliff M includes space measure Mk (k = 1, 2, 3) and time measure M0, which corresponds to a physical linked measure [9].
Quantum mechniasm originated from a canonical commutation relation between different components of cliffs or different cliffs, such as between scalar X and vector Y yielding
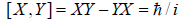 (31)
(31)
where i is the imaginary unit and ℏ is the reduced Planck's constant (ℏ =h/2π).
For any operator X on Hilbert space, when <X>=<M|X|M> and (ΔX)2 = <X2> – <X>2, if <XY+YX> – 2<X><Y>=0 for any measure Y, one always has real Heisenberg uncertainty relation
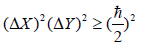 (32)
(32)
The principle produces quantum effects, which also fits duality of particle and wave.
Based on Euler formula
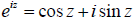 (33)
(33)
we know at z=π
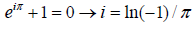 (34)
(34)
This could change our mathematical image. As negative numbers never define logarithm in traditional mathematics, it is suggested to define the logarithm of negative numbers as a probability density of complex numbers in physical space-time
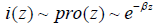 (35)
(35)
where β is a real parameter.
Geometrically, imaginary unit i indicates a 90o rotation in a plane, and it also reveals some distribution of trivial zeros in Riemannian ζ-function, as shown as Figure 2.
Thus, imaginary unit i has its unique meaning, which combine determinative rotation and probability distribution together. In statistical meaning, it is equivalent to distribution density or ensemble function as pro(z) of complex variant z. So a complex measurement in physical system would have probability density
 (36)
(36)
When β=1/kT (k is Boltzmann constant and T is temperature), the probability density is just Maxwell-Boltzmann distribution function.
As the choice of pro(z) is not unique, we may extend it for covering all physical distribution functions including
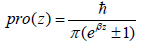 (37)
(37)
which includes Bose-Einstein distribution and Fermi-Dirac distribution when Re(z) = E (energy), as shown as Figure 3.
Combining Eq. (36) and Eq. (37), we write i(z) as
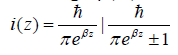 (38)
(38)
For the wave-particle system of E=hν and p=h/λ, the frequency ν or wavelength λ will be estimated as
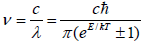 (39)
(39)
This provides a naturally fundamental mechanism of quantum statistics and wave-particle duality.
Statically, the situation resembles that one cliff describes one state. Dynamically, while there are inner relations among z, A and B for describing local features, there are outer relations between cliffs for describing global features.
Physically, a cliff M characterizes a particle or a vortex, where M = (z, A, B) reveals anything that can be characterized by three eigenvalues (z, A, B), and the conjugation M̅ measures its entangled state. While scalar z, vector A and spinor B respectively revealed local information, M and M̅ described global information.
According to the quantum commutation relations, any scalar energy E (t) and vector momentum p (s), linking with time (t) and space (s), construct canonical commutation relations as
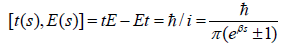 (40)
(40)
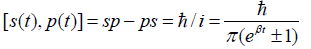 (41)
(41)
The relations imply that the measurement of energy with time changes could produce a system error in space measurement, while the measurement of momentum with space changes could produce a system error in time measurement. This is just the origin of the uncertainty principle.
When we define Z as grand system ensemble based on system ensemble i(z) with probability density pro(z), the free energy F in the system can be calculated as
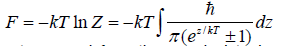 (42)
(42)
and entropy S or information I can be introduced as
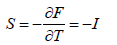 (43)
(43)
then the total energy E of the system will be
dE = dF +TdS + SdT (44)
As information is equivalent to negative entropy, it is possible to recognize quantum information theory [10,11]. The framework penetrates quantum statistical physics.
Meanwhile, as spinors are better than tensors in physical expression [7], the scalar-vector-spinor (SVS) framework will be better than the TeVeS one [12-14] for physical applications. The SVS model as a concise mathematical physical framework is a suitable methodology for studying both micro-particles and macro-galaxies, and we expect to have further explorations.
In quantum mechanics, there is so-called statistical interpretation of a wave function as a complex-valued probability amplitude (wave-vector), which is a mathematical description of the quantum state of an isolated quantum system, as a function of the degrees of freedom corresponding to some maximal set of commuting observables. Once such a representation is chosen, the wave function can be derived from the quantum state. The statistical interpretation had been widely accepted since Born [15,16], and the squared modulus of the wave function is a real number interpreted as the probability density of measuring a particle's being detected at a given place (or having a given momentum) at a given time, and possibly having definite values for discrete degrees of freedom. The integral of this quantity, over all the system's degrees of freedom, has to be 1 in accordance with the probability interpretation. A probability amplitude is a complex number whose modulus squared represents a probability or probability density. For example, the values taken by a normalized wave function ψ are amplitudes, since |ψ(x)|2 gives the probability density at position x.
However, we never knew why the wave function has to link with probability before. Now above mathematical principle interpreted the reason and gave its mechanism completely, via i(z) linking with quantum (ℏ) mechanism and probability density. This is a concise mathematical principle of quantum mechanism.
Philosophically, physicists do always to find simple, natural and symmetric hypothesis as a correct physical theory, so that a good hypothesis, beyond standard models, should abide following three philosophical rules (LMM or 3R) for reaching both truth and beauty [17,18].
R1. Logic harmony: It is better to invent new mathematics, and the mathematical structure approaches the physical essence.
R2. Minimum hypotheses: it needs minimum non-found facts (particles/ fields). It is hoped to introduce less new particles and forces.
R3. Maximum hopes: it matched realities in maximum concordance (it can explains all present experiments/observations and forecast possible phenomena). It is hoped to explain dark sectors and all problems in physics, giving checkable forecasts or falsification mechanism.
These philosophical principles supply a philosophical foundation of physics. Based on mathematical cliffs, quantum scalar-vector-spinor physics is feasible and possible way to approach physical reality.
The quantum mechanism has its mathematical origin and quantum physics based on the mathematical principle, which provides a concise and easy understanding for quantum theory, i.e. the quantum mechanism originates from [X, Y]=XY – YX = ℏ/i. With considering the Euler formula, negative logarithm is also understood as probability distribution, which leads to new understanding of statistical mechanism, yielding quantum statistics. The mathematical principle provides a natural quantum physics characterized by static “one cliff, one state” and dynamic “i(z) generates probability”, in which the conjugation of the cliff reveals its entangled one.
Based on the mathematical principle, together with existed physical principles (action principle, duality principle and equivalence principle as ADE) [18], it is feasible to re-recognize the local-global relations in the mathematical physical system, which imply possible unification of microparticles and macro-galaxies. We expect to stimulate further studies as future work.
This is personal work without any grant, and author acknowledges the anonymous reviewers.
The author declares no competing interests.
Physical Mathematics received 686 citations as per Google Scholar report