A New Number Theory – Questions about Integrals and Derivatives

Luca Sonaglioni^*
*Correspondence: Luca Sonaglioni, Free Professionist, Italy, Tel: 388-0579470, Email:

Keywords

Quaternions · Operator theory ·Algebra · Tensor methods

Introduction

In paper [1,2] we’ve introduced the basis of a (3-n)d commutative algebra.

Given 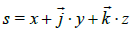s is a point on the space, s can be also written as:

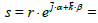
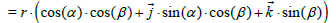
We can asses the differential by algebraic notation or by vector notation:

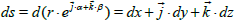
The questions about derivative are a consequence of the non distributive property of this algebra. As we have seen in paper [3], in general the limit

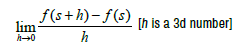
does not exist. So, always in general, we can’t write that

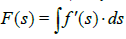
because (most often) the derivative does not exist, and in many cases the product 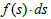is not an exact differential form.

But, we can bypass the problem:

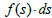in general, is not an exact differential form in the (x,y,z) algebraic notation; 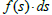is a 3d product and the algebraic development of the 3d product is a complex form (see paper [4]) that, in many cases can’t be reduced to an exact differential form (note that a differential is exact if and only if it is integrable).

We can consider the vector notation and the coordinates (r,α ,β ) , in this case we can write the product 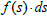as a 3d product in vector notation:

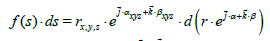
The differential of 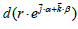is

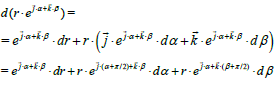
The generic following 3d product:

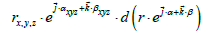
can be an exact differential form.

For simplicity we can consider the 3d product:

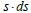
in vector notation become:

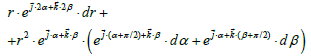
and we can observe that, this 3d product (in vector notation) become an elementary (3d) exponential product, and that it is also an integrable exact form.

So we can say:

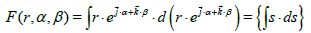
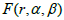is the primitive of s , this is not few.

The 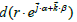as seen above, is exactly the ds in vector notation. We have used this ds to calculate the volume of a sphere (see appendix of paper [2]); it also have to remember that 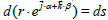. is the infinitesimal vector whose coordinates intercept the elementary volume in the 3d space (Figure 1).

And that 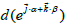is the infinitesimal vector whose coordinates intercept the elementary surface on the sphere of radius 1 (Figure 2).

What does it means all this discussion? It means we do not have the same algebra as the 2d complex algebra but a very similar algebra, it exist the differential of f(s) (if f(s) is made of differentiable functions) or, in other words, we can always calculate the infinitesimal of f(s), but (in general) not the derivative. As an example, for the standard real algebra, we can write:

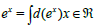can we say the same for this extended (3-n) d algebra? yes, we can 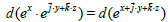is an exact differential, we can say: 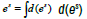is a generative function whose integral converge to es but, we have to observe that d(es) can’t be expressed as a function of s, this is the problem. In a certain point of view we can consider the differential d(es) to be like an extended concept of the derivative of es, but in fact we do not hav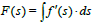e: were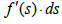 is a 3d algebraic product, we have 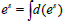were d(es) is a function of (x,y,z), and not a function of s.

Note that the derivative of s exist, and in fact the differential 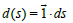is a 3d product (a very simple 3d product), so we can say that 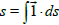s is a primitive of .

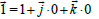We can calculate the differential of d(s²) in algebraic or vector notation, but this is not an expression of s; for s², we can say:

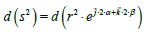(1)

and in general for 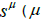is a real constant) we can say:

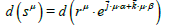(2)

we can calculate the differential of (1) and in general of (2), and we can write:

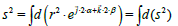
and in general

for e^s we can write

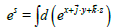
Also, by using the vector notation we can (for example) calculate the primitive:

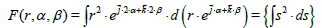
and the primitive:

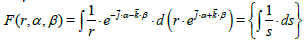
and many other primitive, but these primitives are functions of (r,α ,β ), not functions of s. In general, because the algebraic product is well defined, we can differentiate complex expression, but, (for example) can we say es is the primitive d(es)?, the answer is yes and no. The differential of es is not an expression of s as we have for the 2d complex algebra, the same for the differential of s², we have the infinitesimals whose integral converges to s² and e^s, but they are not the derivative as we have for the 2d complex algebra. The derivative limit, in the sense of a 3d limit, in general, does not exist.

As a conclusion, we can note that most of the problems require a good computational integration method, this algebra permit to integrate many and many expression. As we have seen in paper [5] we do not have problems to integrate expressions. The problem may be what we are looking for with an integral, but to asses the integral, in general, is not a problem.

Conclusion

This algebra is born by the definition of the sum and of the product of two (3-n)d numbers. The sum definition comply exactly with the sum definition of the 1d and 2d complex algebra, the product definition comply with the 1d and 2d complex algebra. The result is a very similar (3-n)d complex algebra, commutative but not distributive.

In the same manner as above (if we can have good definitions), we can discuss about series, successions, functions approximations, convolutions, integral transformations and many well known math problems, but in fact the big argument is: the definition of the (3-n)d product is a good choice? It would seem so.

My intent was to propose an answer about quaternion’s problem; in 1843 William Rowan Hamilton invented a 3d non commutative algebra that has been used for some applications, we think that our idea can be useful for finite element systems (for example), if our approach is faster than the tensors algorithms, and in general, for geometric applications in the 3d space; similarly the extension of the exponential function seems to be a good tool too. We don’t know if this algebra can be useful in relativistic physics, were we have to manage the space-time as a set of four independent variables, but this can be a good challenge about the definition of the (3-n)d product.

References

1. Hime, Henry William Lovett. The outlines of quaternions Longman Greens. (1894).
2. Sonaglioni. A New Number Theory. J Appl Computat Math 4 (2015): 212.
3. Sonaglioni L. A New Number Theory - Algebra Analysis. J Appl Computat Math 4 (2015): 267.
4. Sonaglioni L. A New Number Theory-Algebra Analysis II. J Appl Computat Math 5 (2016): 289.
5. Sonaglioni L. “2168-9679-7-metricconverterProductID427 A427 A New Number Theory: Considerations about the (3-n)d Algebra”. (2018).