Activated Carbon Pellets from Date Palm Leaves (Phoenix dactylifera L.) Prepared by Chemical Activations: Specific Surface Area, Young's Modulus and Spring Length Between Two Cubic Granular Volume Structures Estimated by X-ray Diffraction Analysis

Fatima Musbah Abbas^1*, Abubaker Elsheikh Abdelrahman² and Abdul Kariem Arof^3
*Correspondence: Fatima Musbah Abbas, King Khalid University, Collage Science and Art, Dhahran Al-Janoub, Saudia Arabia and Biotechnology and Genetic Engineering, National Researcher, Khartoum, Sudan, Email:

Keywords

Date palm leaves • Activated carbon pellets • KOH • Crystallites parameters • Specific surface area • Young’s modulus • Spring length

Introduction

Date palm leaves (Phoenix dactylifera L.) are classified as lignocelluloses, biomass material composed of cellulose, hemicelluloses, and lignin as main products, with high carbon and low- ash contents. Also, it has several advantages, such as its abundant, low cost, and ability to be produced in large amounts and for commercial benefit, has been used to make baskets, fans, crates, boxes, and hats.

Activated carbon (AC) refers to a range of porous materials manufactured to show an exceptionally high internal surface area and pore structure [1]. Activated carbon containing micro-pores or medium pores have been widely used for catalyst and catalyst support [2], wastewater treatments [3], double layer capacitors [4], electrodes [5] and higher energy storage super- capacitors [6,7]. Activated carbon material is generally available in three main forms; these are powder, granular and pellet forms [8]. The pellet form is particularly useful because it is dense or contains particle sizes closed together in a solid manner [9,10]. There are two methods for preparation of activated carbon: physical and chemical methods. A chemical method is widely used to prepare activated carbon, which involves mixing carbonaceous material with dehydrating agents to facilitate surface properties at relatively stable temperatures [8]. The use of KOH for the activation of the biomass materials to prepare high surface area porous carbon has been known [11-14]. Analysis of activated carbon structure can be made in terms of crystallites parameters (L_c, L_a and d₀₀₂) of the graphiticlike crystallites that are randomly distributed and oriented throughout the sample. Small crystallite perimeters reflect to disorder a structure which is sensitive to higher porosity content [15]. There are several methods for empirical modeling for porous media in terms of mathematical methods [16,17]. As example, the crystallites parameter (L_c) and bulk density were used to estimate the specific surface area for activated carbon [18]. Several attempts have been made to improve the properties of carbon materials such as mechanical properties [19], crystallite structures [20] microspores and mesopores structures [19] and specific surface area and total pore volume [21]. It has been found that Young’s modulus of carbon pellets increased linearly with the molarity of the acid used to treat self-adhesive carbon grains (SACG) from oil palm empty bunches [22]. An empirical method proposed by Emmerich FG and Luengo CA [1] considers that carbon is composed of two phases, a granular structure of (micro to crystallites and cross-links). The application of this method consists in determining the Young's modulus and spring length between the cubic granular volume structures of the carbon samples from its crystallite parameters as a function of heat treatment temperature. This method has been applied to estimate Young’s modulus of carbon pellets as a function of compression pressure by assuming that the behavior of Young’s modulus with respect to the compression pressure has a similar behavior with respect to the heat treatment temperature [19] and proved to be accurate to estimate Young’s modulus of the carbon materials. So far, on the present work date, palm leaves have been used as a starting material for the preparation of activated carbon by chemical activation. Initially, palm leaves were heated at a low temperature, milled to fine grain powder for 50 hours a milling time, to improve its self-adhesive properties [9] and activated with KOH agent to prepare the activated carbon with a good crystalline structure and mechanical properties.

The objective of this work is to characterize the crystallite parameters, Young’s modulus and spring length between two cubic granular volume structures, empirically by Emmerich FG and Luengo CA [1], and modified, given by Fatima MA, et al. [19], by assuming that the behaviors of Young’s modulus with respect to KOH concentration the has a similar behavior with respect to the compression pressure. An X-ray diffraction program (Trace Version 5) was used to calculate the crystallite parameters to assess the accuracy of measurements, and the results were compared to the review data.

Materials and Methods

Sample preparation

Date palm leaves (Phoenix dactylifera L.) were initially washed thoroughly to remove contamination and dried at 100°C. The palm leaves were pre-carbonized in a vacuum chamber (Eyela, A-35) at 280°C for four hours, to cause them to shrink and break the palm leaves microstructure and release non-carbon content [23]. Then the Pre- carbonized palm leaves were milled for 50 hours to produce fine grain powder of ≤ 10 particle sizes to improve it is self-adhesive grain powder properties as displayed in (Figure 1). About 250 g of self-adhesive grain powder was impregnated in 100 ml KOH, having concentrations of 0.0, 0.08, 0.09 0.10, 0.15, 0.20, 0.25, 0.30 and 0.35 by moles (M). The mixture was magnetically stirred for two hours and kept in the mixture for 16 hours, before being dried in an oven at 100°C for 24 hours. The dried mix was further milled for five hours and sieved again. 2 g of each self-adhesive powder was pelletized as grain pellets by applying 12 metric tons of pressure in a mold of 2.75 cm in diameter and 8.5 cm in length. All grain pellets then exhibited an excellent binding property and were characterized by bulk density and elastic ultrasonic techniques before being carbonized at 700°C in a nitrogen environment (Vulcan Box Furnace 3-1750) using a multi-step heating profile: starting at 1°C/min from room temperature to 375°C, where it was held for 1 h before heating was resumed at 3°C/min to 700°C, where it was finally held for 5 min. The system was automatically allowed to cool down naturally to room temperature. The obtained activated carbon pellets were first washed with dilute hydrochloric acid and then washed with hot distilled water until a pH of 5 and dried at 100oC for 4 hours. Measurements of the grain pellets' and activated carbon pellets' dimensions were carried out using a micrometer. The bulk density was determined by dividing the weight of the sample by its volume. The bulk density was the overall density, inclusive of solid carbon and pore spaces. Results are given as the average of 5 replicates of each piece and analyzed as a function of KOH concentration. The particle size distribution of the green powder produced was measured by operating the Microtrac-X100 machine. The operating principle of the Microtrac-X100 machine is based on the photo-extinction phenomenon and Stokes law sedimentation theory. The XRD diffraction profiles of the activated carbon pellets sample were analyzed using an X- ray diffract meter (Bruker Advanced Solution AXS D8) operated at 40 kV and 30 mA with Cu Kα X-ray radiation with 1.54 Å wavelength, scanned over an angle of (10o-60oC), with a step size of 0.04oC. The diffraction spectrum was corrected for the instrumental line broadening and fitted into a symmetrical Gaussian distribution curve. The crystallite parameters were calculated from the full width at half maximum (FWHM) of the (002) and (100) reflection peaks by Bragg’s and Deby- Sherrier Equations [24]. An X-ray diffraction program (Trace 1.4 Varian 5 from Diffraction Technology PTG LTD, Australia) was used to calculate the crystallite parameters profile.

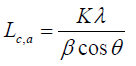(1)

Where,

θ = The scattering angle position

λ = The wavelength of X-ray diffraction

K = A shape factor whichis equal to 0.94 for L_c and 1.84 for L_a

β = The width of a reflection at half-height expressed in radians.

The Specific surface area (SSA) was estimated empirically crystallite parameter (L_c) and the bulk density (ρ) using the mathematical equation proposed by Dresselhaus MS, et al. [18] as:

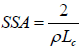(2)

Young’s modulus of the activated carbon pellets samples was determined using an Ultrasonic Pulsar-Receiver (Model 500 PR) operating at 25 MHZ and equipped with PICO ADC-200 software. The pulsar division produces electrical pulses converted into ultrasonic signals using identical transducers. Petroleum jelly was applied as a coupling medium at the interface of the probe-sample. A reference glassy carbon (Sigradur K) (SIG-K) was used to calibrate the ultrasonic signal and measure the samples' Young’s modulus (E). The measure of the SIG-KK) agreed with the value given by the supplier with an error of < 1%. Then, Young’s modulus (E) of the one-dimensional form of the wave equation in a weakly attenuation region [19] is given as:

E = ρV² (3)

Where,

Ρ = The bulk density of the sample

V = The longitudinal velocity of the sample

Empirical method

Emmerich FG and Luengo CA [1] empirical method to correlate Young’s Modulus (E) with the crystallite parameters (L_c, L_a and d₀₀₂) and volume fraction (X) for the carbon materials as a function of their heat treatment temperature via the estimated diagram of a cubic granular volume structures displayed in (Figure 5) as follows Where i is the initial value, in order to fit this model in our AC samples it is necessary to estimate the initial X-ray diffraction data, for the untreated AC pellets (0.0 M) has been used as an initial value in this work. Finally, Equation 4 subdivides as the following:

(4)

The spring length (SP) between two cubic granular volume structures (Figure 5) is given as:

Where,

γ = Constant related to force and represents the degree of stiffness of the sample

L = The cube root of the mean granular volume structure, equal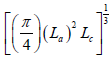

X = The volume fraction of the sample, can be given as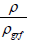

ρgrf = The bulk density of pure graphite (2.26 gm^-3)

n = Is an integer defines the order of change, given as:

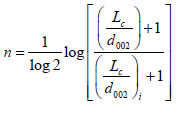(5)

Where, i is the initial value, in order to fit this model in our AC samples it is necessary to estimate the initial X-ray diffraction data, for the untreated AC pellets (0.0 M) has been used as an initial value in this work. Finally, Equation 4 subdivides as the following:

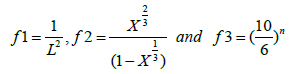(6)

The spring length (SP) between two cubic granular volume structures (Figure 5) is given as:

(7)

Results and Discussion

Carbonization process

The particle size distributions of the GP produced for 50 hours are shown in Figure 1. The grain powder shows different distributions, which are obviously not symmetrical but skewed towards the lower sizes of ≤ 10 microns (μ), with a maximum dominant range of 5 (μ) and 3 (μ), which have been used to prepare activated carbon pellets. During the carbonization of the grain pellets, a large weight loss and volume change occurred, with the body physically shrinking to maintain its structural integrity because of the release of the non-carbon contents and volatile components [23], casing to reduce the bulk density of the activated carbon produced (Figure 1).

X-ray diffraction

Figure 2 shows the X-ray diffraction profile diffraction intensity, initially at (002) and (100) broad and overlapped (002) and (100) Bragg’s reflection intensity results of non-graphic structure [25]. Similar observations have been shown on solid carbon pellets prepared from pre-carbonized date palm leaves by compression pressure [19] and activated carbon from Sago plant [5]. The diffraction profile has been corrected to the background line and fitted to the Gaussian distribution curve, as shown in Figure 2.

As the diffraction intensity profile overlaps and consists of four broad peaks intensity, i.e., (101), (002), (100) and (004), located at approximately 13.55°C, 24.2°C, 43.59°C and 52.0°C diffraction angles, respectively. After correction, the diffraction intensity and Bragg’s peaks were the same as in a graphite-like structure and the layer separation was slightly further apart than in a graphite structure as shown in Figure 2 (Figure 2).

The results of crystallite parameters (L_c, L_a and d₀₀₂) were calculated from Bragg’s peak intensity, using Deby-Sherrier and Bragg’s equations, which are summarized in Table 1 and Figure 3. The d₀₀₂ is greater than that of pure graphite (i.e., d₀₀₂ = 3.354 Å), indicating that non- graphite or tubostratic structure (Li, et al.). This value is closed to those of commercial activated carbon (AC-Helsa) (3.76) and (AC-Tye H) (Kristin, et al.). The value of L_c is found to be ~10 Å, corresponding to ~ three layers of graphene, (each layer of graphene is at the c-axis of 3.35 Å). It is also equivalent to that of commercial activated carbon (AC-Helsa) as shown in Table 1. This Table 1 did not show any significant change of Lc in the c-axis, while the La growth with increasing the KOH concentration as shown in Figure 3 indicates that KOH concentration caused to improve in the crystalline structure in the samples. These values are equivalent to those of commercial activated carbon (AC-Type H) [25]. Additionally, the La values is similar to those of solid carbon pellets from date palm leaves prepaid as a function with compression pressure, while the Lc values is less (Fatima, et al. bas shown in Table 1 (Table 1 and Figure 3).

Specific surface area (SSA)

Table 1, shows such KOH concentrations can produce CPs with a specific surface area of (1440.0 m²/g-1683.5 m²/g) with an acceptable pore structure, which is in agreement with the nonporous carbon from oil palm leaves activated with KOH of 1685 m²/g [26] and a higher than those from grape seed activated by KOH (1222 m²/g) [27]. This implies that the KOH treatment can synthesize CPs with a highly specific surface that could be used in a wide range of applications, such as higher adsorption properties and a super-capacitor electrode. The final results indicate that KOH activation causes an improvement in a specific surface area of the AC produced.

Young’s modulus

Table 1 shows the densities of the AC increased rapidly and then decreased with a higher concentration of KOH. 0.25 M KOH concentration is a higher bulk density compared to the other, which is required to produce dense activated carbon pellets. Table 2 and Figure 4 show that Young’s modulus (E) of the ACPs increased slightly from 5.35 GPa to 10.53 GPa which is in the range of those in solid carbon pellets from date palm leaves prepared at different compression pressure of (5 GPa-7.1 GPa) [19]. Indicating that both KOH and compression pressure have similar effects. It agrees well with our summation of the behavior of KOH concentration. It has similar behavior to the compression pressure. 0.25 M is the higher value of E (10.53 GPS) than the others. Justifying that KOH activation improves the mechanical performance of the grain powder and improves the optimal activation that can be used to activate the grain powders of palm leaves. Similar behavior has been found that Young’s modulus of carbon pellets increased y with the molarity of the acid used to treat self-adhesive carbon grains (SACG) from oil palm empty bunches [22] and cotton cellulose [10].

Above 0.25 M KOH, E decreased, possibly due to the increased porosity of the AC samples. Additionally, the wash process removes the noncarbon content from the CPs to create new pores, lowering the mechanical properties in the AC-produced process. The amount obtained for our ACs samples is only 20–33% of SIG-K., indicating that our ACs sample is porous compared to that of glassy carbon SIG- K (Figure 4).

Emmerich and Luengo (Empirical methods)

The crystallite parameters L_a, L_c and d₀₀₂ and the volume fraction (X) were substituted for equation 3 to estimate the E₂ by adjusting the values of γ until matching the E values as shown in Figure 5, with reasonably a good fitting value of (γ = 0.91) representing the degree of stiffness the estimated E₂ values is matching the experimental E values measured by ultrasonic techniques. The fitting data also shows that below 0.10 M KOH activation are not well matched, possibly the crystallite parameters of the AC are not built yet or not formed. All the fitted parameters (E, f1, f2, f3, X and E₂) are presented in Table 2. Justifying that AC produced is seen to be composed of two phases. A granular structure (of micro to crystallites in cross-links) with internal structure of micropores/mesopores, indicating that such structures are strongly affected by the KOH activations. Finally, these results could explain the applicability of empirical methods to estimate the mechanical properties of the AC materials (Table 2 and Figure 5).

Spring length (S_p)

Spring length (Sp) between the cubic granular volumes structures (Figure 6) and the data are presented in Table 2 and plotted as a function of KOH concentrations in Figure 7. The data in this Figure 7 clearly show that the S_p has a fluctuating behavior as a function of KOH treatments in fluctuations of (4.8-3.74 Å). Showing that 0.25 M is a much lower spring length, that is very close to average interlayer spacing, d₀₀₂ (i.e., 3.72 Å = 0.372 nm), justifies the heterogeneous nature of a high-energy absorption from the pelletizing load and the carbonization temperature on a microscopic scale than the others. This result is consistent with the higher value of Young’s modulus (10.5 GPa) of the AC sample at 0.25 M concentrations. The visual inspection giving 0.25 M is the optimum for activating the grain powder, but the internal microstructure of the S_p at a critical length, which is structural, cannot be equal to the crystallite unit (d₀₀₂). It probably collapses if the grain pellets undergo a compassionate pressure above 12 metric tons and/or above 700oC carbonization temperature. These results could be explained by the reason of some broken carbon samples when they were treated with a higher KOH concentration (i.e., 0.4-0.5 M) and carbonized above 700oC as well as during the washing process with hot distilled water and/or diluted acid concentration. Then we consider that this model is imported to characterize the mechanical behavior of carbon material from its microscopic scale. Otherwise, it is another method for microstructure characterization to avoid cracks or collapse in the manufacturing of carbon and composited carbon electrodes in thermo-thermo-heating applications (Figures 6 and 7).

Conclusion

Activated carbon pellets (ACPs) from date palm leaves (DPLs) were prepared by chemical activation. DPLs are heated at low temperature and converted to fine grain powder, to improve self-adhesive carbon grains. X-ray diffraction data showing the structure of AC samples is non- graphic. The stack diameter increased with increasing KOH concentration. The palm leaves can prepare activated carbon in pellet form with a high specific surface area characteristic. Indicating that the KOH concentration and multi-step heating profiles play the main role in improving the surface area in the AC produced. Young's modulus increased with increasing KOH concentration, reaching its maximum at 0.25 M KOH. Young’s modulus (E) measured by ultrasonic techniques is in good agreement with those estimated empirically from the crystallite parameters (E₂). The spring length S_p fluctuates and its value is close to that of the crystallite parameter, d₀₀₂ which is considered as a critical length and the sample could collapse if it undergoes a higher load or heat treatment temperature at 0.25 M KOH, which is in agreement with the higher Young’s modulus of the AC sample.

Acknowledgement

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under grant number (GRO/323/43- 1443) and acknowledge to Act Centre for great support.

Conflict of Interest

None.

References

1. Emmerich, F. G. and C. A. Luengo. "Young's modulus of heat-treated carbons: A theory for nongraphitizing carbons."Carbon31 (1993): 333-339.

Google Scholar, Crossref, Indexed at

2. Lam, Edmond and John HT Luong. "Carbon materials as catalyst supports and catalysts in the transformation of biomass to fuels and chemicals."ACS Catal 4 (2014): 3393-3410.

Google Scholar, Crossref, Indexed at

3. Ahmed, Muthanna J. "Preparation of activated carbons from date (Phoenix dactylifera L.) palm stones and application for wastewater treatments."Process Saf Environ Prot102 (2016): 168-182.

Google Scholar, Crossref, Indexed at

4. Song, Xinyu, Xinlong Ma, Yun Li and Liang Ding, et al. "Tea waste derived microporous active carbon with enhanced double-layer supercapacitor behaviors."Appl Surf Sci 487 (2019): 189-197.

Google Scholar, Crossref, Indexed at

5. Farma, Rakhmawati, Syarifah Famela Maurani, Irma Apriyani and Ari Sulistyo Rini. "Fabrication of carbon electrodes from sago midrib biomass with chemical variation for supercapacitor cell application." J Phys Conf Ser 2049 (2021): 012054.

Google Scholar, Crossref, Indexed at

6. Ahmed, Sultan, Ahsan Ahmed and M. Rafat. "Investigation on activated carbon derived from biomass Butnea monosperma and its application as a high performance supercapacitor electrode."J Energy Storage 26 (2019): 100988.

Google Scholar, Crossref, Indexed at

7. Boujibar, O., Ghosh A., Achak O. and Chafik T., et al. "A higher energy storage super-cpacitor based on nano-porous activated carbon electrode made from argon shells with excellent ion transport in aqueous and non-aqueous electrolytes." J Energy Storage 26 (2019): 100958-100966.
8. Tadda, M. Abubakar, Amimul Ahsan, Abubakar Shitu and Moetaz ElSergany, et al. "A review on activated carbon: Process, application and prospects."J Adv Res Civ Eng 2 (2016): 7-13.

Google Scholar, Indexed at

9. Deraman, M., Rahul Omar, Sarani Zakaria and Mardin Talib, et al. "Hardness and microstructure of carbon pellets from self‐adhesive pyropolymer prepared from acid and alkaline‐treated oil palm bunch."Adv Polym Technol 23 (2004): 51-58.

Google Scholar, Crossref, Indexed at

10. Abubaker, E. A., Mohamad D. Ramli O., Mohd-Hafizuddin J. Ramli O. and Sarani Z., et al. "Young’s modulus, hardness and crystallite size of carbon pellets prepared from HCL treated pre-carbonized cotton ball." Solid State Sci Technol 12 (2005): 281-289.
11. Gil, R. R., B. Ruiz, M. S. Lozano and E. Fuente. "Influence of the pyrolysis step and the tanning process on KOH-activated carbons from biocollagenic wastes. Prospects as adsorbent for CO2 capture."J Anal Appl Pyrolysis 110 (2014): 194-204.

Google Scholar, Crossref, Indexed at

12. Yakout, S. M. and G. Sharaf El-Deen. "Characterization of activated carbon prepared by phosphoric acid activation of olive stones."Arab J Chem 9 (2016): S1155-S1162.

Google Scholar, Crossref, Indexed at

13. Yang, H. M., D. H. Zhang, Y. Chen and M. J. Ran, et al. "Study on the application of KOH to produce activated carbon to realize the utilization of distiller’s grains." IOP Conf Ser: Earth Environ 69 (2017): 012051.

Google Scholar, Crossref, Indexed at

14. Nguyen, K. N., Wein-Doo Y., Zenja C. and Hoai L. T. "Influence of activation temperature of the structural properties of Ac Xerogels and electrochemical performance." Advance in Matr Sci 9 (2017): 8308612.
15. Benedetti, Vittoria, Francesco Patuzzi and Marco Baratieri. "Characterization of char from biomass gasification and its similarities with activated carbon in adsorption applications."Appl Energy227 (2018): 92-99.

Google Scholar, Crossref, Indexed at

16. Alasfar, Reema H., Said Ahzi, Nicolas Barth and Viktor Kochkodan, et al. "A review on the modeling of the elastic modulus and yield stress of polymers and polymer nanocomposites: effect of temperature, loading rate and porosity."Polymer14 (2022): 360.

Google Scholar, Crossref, Indexed at

17. Jionhao, C., Liehui Z. and Wei W. "Modeling flow transport in variable saturated porous media: Theory percolation and and effective medium approximation." Elsevier (2021): 79-117.
18. Dresselhaus, M. S., A. W. P. Fung, A. M. Rao and S. L. Di Vittorio, et al. "New characterization techniques for activated carbon fibers."Carbon30 (1992): 1065-1073.

Google Scholar, Crossref, Indexed at

19. Fatima, M. A., Zehhba A. A., Rehab O. E. and Abubaker E. A. "Characterization of pores size, surface area and fractal dimensions of activated carbon powder prepared from date palm leaves." Mol Bio 11 (2022a): 352.
20. Abdelrahman, Abubaker Elsheikh and Co-Author Dr Selma Elsheikh Abdelrahman. "Crystallites dimensions and electrical conductivity of Solid Carbon Pellets (SCPs) from date palm leaves (Phoenix dactylifera L.)."J Res Sci 4 (2023).

Google Scholar, Crossref, Indexed at

21. Yi, Hyeonseok, Koji Nakabayashi, Seong-Ho Yoon and Jin Miyawaki. "Pressurized physical activation: A simple production method for activated carbon with a highly developed pore structure."Carbon183 (2021): 735-742.

Google Scholar, Crossref, Indexed at

22. Deraman, M., Rahul Omar, Sarani Zakaria and Izan R. Mustapa, et al. "Electrical and mechanical properties of carbon pellets from acid (HNO3) treated self-adhesive carbon grain from oil palm empty fruit bunch."J Mater Sci 37 (2002): 3329-3335.

Google Scholar, Crossref, Indexed at

23. Dhyani, Vaibhav and Thallada Bhaskar. "A comprehensive review on the pyrolysis of lignocellulosic biomass."Renew Energ 129 (2018): 695-716.

Google Scholar, Crossref, Indexed at

24. Song, Dangyu, Cunbei Yang, Xiaokui Zhang and Xianbo Su, et al. "Structure of the organic crystallite unit in coal as determined by X-ray diffraction."Min Sci Technol 21 (2011): 667-671.

Google Scholar, Crossref, Indexed at

25. Faber, Kristin, Felix Badaczewski, Wilhelm Ruland and Bernd M. Smarsly. "Investigation of the microstructure of disordered, non‐graphitic carbons by an advanced analysis method for wide‐angle x‐ray scattering."Z fur Anorg Allg Chem 640 (2014): 3107-3117.

Google Scholar, Crossref, Indexed at

26. Chanpee, Sirayu, Napat Kaewtrakulchai, Narathon Khemasiri and Apiluck Eiad-Ua, et al. "Nanoporous carbon from oil palm leaves via hydrothermal carbonization-combined KOH activation for paraquat removal."Mol 27 (2022): 5309.

Google Scholar, Crossref, Indexed at

27. Okman, Irem, Selhan Karagöz, Turgay Tay and Murat Erdem. "Activated carbons from grape seeds by chemical activation with potassium carbonate and potassium hydroxide."Appl Surf Sci293 (2014): 138-142.

Google Scholar, Crossref, Indexed at