Advanced Neural Networks for All Terminal Network Reliability Estimation: A Mini-Review

Om Prakash Yadav^* and Alex Davila-Frias
^*Correspondence: Om Prakash Yadav, Department of Industrial and Manufacturing Engineering, North Dakota State University, Fargo, USA, Email:

Keywords

All-terminal • Network reliability • Convolutional neural networks • Deep neural networks

Introduction

Usually, networks represent critical infrastructure systems such as communication networks, piping systems or power supply systems. Therefore, reliability assessment of these critical networks is imperative. A network can be defined as a set of items (nodes or vertices) connected by edges or links. Graphical models allow to visualize the interdependencies of the components in a system. Nodes characterize components and junctions of the system, and edges represent the connections. For example, busbars in power systems or switches in telecommunication systems are modelled by nodes, whereas edges characterize power lines in power systems and optical fibers in telecommunication systems. Such graphical models are commonly based on Graph Theory (GT), where a graph G (N, L) denotes the graph G composed by the set N of nodes and the set L of links or edges.

Regardless the number of nodes, links, or their interconnection, the network reliability has several definitions; most of them are associated with connectivity [1]. Three popular measures are all-terminal, two-terminal and k-terminal [2]. All-terminal reliability is the probability that every node can communicate with every other node in the network. The two-terminal reliability problem requires that a pair of specified nodes, e.g. source (s) and terminal (t), be able to communicate with one another. K-terminal reliability requires that a specified set of k target nodes be able to communicate with one another. Because the two-terminal reliability problem is simpler than the all-terminal reliability one and the k-terminal reliability is indeed a subset of all-terminal reliability with a space set restricted to k nodes only, advanced network reliability techniques are focused on the all-terminal reliability [3, 4].

All-terminal exact reliability is however, an NP-hard problem which has led to the search of approximated but more efficient methods [3, 5]. As a part of the Machine Learning (ML) techniques, Artificial Neural Networks (ANNs) have emerged as a promissory tool to estimate network reliability. ANNs have been usually trained with the network topology and link reliability as inputs and with the target network reliability as desired output [3, 4]. For example, they utilized an ANN to predict the All-Terminal Network Reliability (ATNR) with the network architecture, the link reliability, and the reliability upper bound as inputs, and the exact network reliability as the target [3]. More recently, they proposed an ANN model to predict the ATNR [4]. Such models take the upper bound network reliability among other inputs to predict the network reliability.

Traditional ANNs have evolved into Deep Learning (DL) approaches such as Deep Neural Networks (DNNs), Convolutional Neural Networks (CNNs) and Recurrent Neural Network (RNNs). Although DL has been applied for reliability estimation, little evidence is available of its use for network reliability estimation.

The aim of this mini-review is to compare the performance of our recently proposed methods based on advanced neural networks techniques such as CNNs and DNNs for the ATNR estimation problem. CNNs have been successful in image classification [6-8]. Therefore, appropriate formatting is needed to convert the networks features such as adjacency matrix and topological attributes to an image-like matrix. Also, a regression layer with sigmoid activation function has proven to be effective for CNN regression of ATNR [6]. Similarly, DNNs with Graph Embedding Methods (GEM) for pre-processing have shown effectiveness in ATNR estimation [7]. More recently, an integration of DNN and Monte Carlo (MC) allowed accurate ATNR of large networks [8]. In this paper, we briefly summarize the use of advanced neural networks such as CNNs and DNNs for network reliability estimation and compare their performance with the results achieved by previous approaches based on traditional ANNs.

In the rest of the article, to avoid confusion, the CNN(s) and DNN(s) acronyms will be used to refer to artificial convolutional or deep neural network(s), respectively, whereas the term network(s) will be employed for the network(s) whose reliability estimation is estimated. The remainder of this article is organized as follows: in the section 2, the CNN and DNN methods are summarized. In section 3, we present a comparison of the results achieved by traditional ANN, CNN and DNN methods. Conclusions and future research directions are exposed in the section 4.

Advanced Neural Networks for All-Terminal Network Reliability Prediction

A network is modelled by a probabilistic graph G= (N, L, p), where N is the set of nodes, L is the set of links, and p is the links reliability.

At any time, only some links of G might be operational. A state of G is a sub-graph (N, L'), where L' is the set of operational links, L' ⊆ L. The all- terminal network reliability of state L' ⊆ L is [9]:

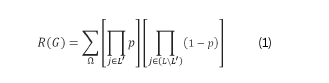
Where, Ω is the set of all operational state

CNNs for ATNR estimation

Convolutional Neural Networks (CNNs) are a specialized kind of artificial neural networks suitable for processing data with a grid-like topology, such as image data. This type of networks applies the mathematical operation convolution in place of general matrix multiplication in at least one of their layers [10]. They proposed a CNN approach to estimate the all-terminal reliability of networks with a given number of nodes and a given set of possible links reliability values [6]. The network information is stacked in a multidimensional matrix to meet the “image” format that a CNN can process. A successful input format consists of layers of two-dimensional matrices concatenated along the third dimension [6]. In the first layer, there is the adjacency matrix. Furthermore, the diagonal of zeros of the adjacency matrix is replaced by the node degree. The second layer is a diagonal matrix with the clustering coefficient. The third layer is a diagonal matrix with the links reliability. The resultant input format for each network is therefore a n × n × 3 matrix, i.e., a three-dimensional matrix. It shows the proposed CNN scheme (Figure 1).

Several combinations of architectures and hyper parameters were tested in a dataset. The performance was measured in terms of the Root Mean Square Error (RMSE) considering cross-validation. The best CNN achieved a RMSE of 0.05079, which outperformed the general ANN proposed by them, who reported an RMSE of 0.06260 [3]. The better performance might be attributed in part to the multiple hidden layers of the CNN instead of only one hidden layer in the standard ANN architecture [3, 4]. In addition, features such as momentum training, dropout and regularization are believed to enable higher predictive accuracy compared to typical ANNs [11, 12]. The improvement in accuracy was attained without the need of providing the upper bound reliability as an input to the CNN.

DNNs for ATNR estimation

Motivated by the good results of CNNs and with the aim to overcome the limitation of fixed size networks (required in the CNN approach), other advanced DL approaches such as DNNs were explored [7, 8]. For instance, instead of an image-like format, DNNs require vector inputs. Therefore, to translate the network information, GEM was investigated, and the RMSE was 0.01069 [7]. Illustrates the DNN approach (Figure 2). Recently, an integration of DNN and Monte Carlo (MC) was proposed that relax the common assumption of perfect nodes [8]. Moreover, this approach allows estimating the reliability of large networks. However, it requires training for a specific network for further prediction of ATNR, given new values of links and nodes reliability. The RMSE in the worst case was 0.02213 for a network with 158 nodes and 189 links.

Discussion

In this section, we briefly compare the performance of traditional ANNs, CNNs, and DNNs in terms of RMSE, execution time, capability of ATNR prediction for networks with varying sizes, need of upper bound input, and assumption of perfect nodes. Comparison is summarized in Table 1. In general, modern approaches such as CNNs and DNNs outperform ANNs in accuracy (RMSE). However, among advanced neural networks there are trade-offs. For instance, DNN is more accurate and flexible (allowing varying sizes) than CNN but slower as well. Similarly, DNN-MC approach is the fastest, allows relaxing perfect nodes assumption and is applicable for large networks, but it needs specific training for each network.

Conclusion and Future Research

This study has compared traditional ANN with modern CNN and DNN approaches to estimate the ATNR. In general, CNN and DNN outperform ANN. Nevertheless, the selection of an appropriate method for a particular application will depend on the preferred features, e.g., execution time, varying sizes prediction, perfect nodes assumption, etc. There are still opportunities for improvement, e.g., accuracy and execution time. Refining pre-processing and input methods to consider imperfect nodes could be useful to enhance current CNN or DNN approaches. In addition, novel techniques such as Graph Neural Networks (GNN) will be explored in search of such improvements.

Conflict of Interest

Author has nothing to disclose.

References

1. Zhang, Zuyuan, Wei An and Fangming Shao. “Cascading Failures on Reliability in Cyber-Physical System.” IEEE Trans Reliab 65(2016):1745-1754.
2. Shooman, Andrew Michael and Aaron Kershenbaum. “Exact Graph-Reduction Algorithms for Network Reliability Analysis.” IEEE Global Telecommun Conf 1 (1991):1412-1420.
3. Ratana, Chat Srivaree, Abdullah Konak and Alice E. Smith. “Estimation of All-Terminal Network Reliability Using an Artificial Neural Network.” Comput Oper Res 29(2002):849-868.
4. Altiparmak, Fulya, Berna Dengiz and Alice Smith. “A General Neural Network Model for Estimating Telecommunications Network Reliability.” IEEE Trans Reliab 58(2009):2-9.
5. Shooman, Martin L. Reliability of Computer Systems and Networks: Fault Tolerance, Analysis, and Design.Hoboken: John Wiley & Sons, USA, (2003).
6. Frias, Alex Davila and Om Prakash Yadav. “All-Terminal Network Reliability Estimation Using Convolutional Neural Networks.” J Risk Reliab 1(2020): 1-20.
7. Frias, Alex Davila, Saeed Salem and Om Prakash Yadav. “Deep Neural Networks for All-Terminal Network Reliability Estimation.” Annu Reliab Maintainability Symp 1(2021):1-15.
8. Frias, Alex Davila, Om Prakash Yadav, Saeed Salem, and Bimal Nepal. “All-Terminal Network Reliability Estimation with Monte Carlo and Deep Neural Networks.” Proc IISE Annu Conf 1(2021): 169-174.
9. Altiparmak, Fulya, Berna Dengiz and Alice E Smith. “Reliability Optimization of Computer Communication Networks Using Genetic Algorithms.” IEEE Int Conf Sys Man Cybern 5(1998):4676-4681.
10. Goodfellow, Ian, Yoshua Bengio and Aaron Courville. Deep learning. Cambridge: MIT press, USA, (2016).
11. Qian, Ning. “On the Momentum Term in Gradient Descent Learning Algorithms.” Neural Netw 12 (1999):145-151.
12. Khumprom, Phattara and Nita Yodo. “A Data-Driven Predictive Prognostic Model for Lithium-Ion Batteries Based on a Deep Learning Algorithm.” Energies 12(2019):660.