Research - (2020) Volume 9, Issue 3
Received: 15-Apr-2020
Published:
01-May-2020
, DOI: 10.37421/2168-9679.2020.9.449
Citation: Jianxin Zhu, Luying Li. An Efficient Solver of Eigenmodes for a Class of Complex Optical Waveguides. J Appl Computat Math 9 (2020) doi: 10.37421/jacm.2020.9.449
Copyright: © 2020 Jianxin Zhu, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In this paper, for a class of complex optical waveguide, the high-precision computation of the propagation constants β are studied. The corresponding Sturm-Liouville (S-L) problem is represented as 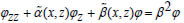 in an open domain (open on one side), where x is a given value. Firstly, a perfectly matched layer is used
to terminate the open domain. Secondly, both the equation and the complex coordinate stretching transformations are constructed. Thirdly, the S-L problem is turned to a simplified form such as
in an open domain (open on one side), where x is a given value. Firstly, a perfectly matched layer is used
to terminate the open domain. Secondly, both the equation and the complex coordinate stretching transformations are constructed. Thirdly, the S-L problem is turned to a simplified form such as 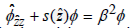 in a bounded domain. Finally, the coefficient function
in a bounded domain. Finally, the coefficient function 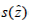 is approximated by a piecewise polynomial of degree two. Since the simplified equation in each layer can be solved analytically by the Kummer functions, the approximate dispersion equation is established to the TE case. When the coefficient function is continuous, the approximate solutions converge fast to the exact ones, as the maximum value of the subinterval sizes tends to zero. Numerical simulations show that high-precision eigenmodes may be obtained by the Müller's method with suitable initial values.
is approximated by a piecewise polynomial of degree two. Since the simplified equation in each layer can be solved analytically by the Kummer functions, the approximate dispersion equation is established to the TE case. When the coefficient function is continuous, the approximate solutions converge fast to the exact ones, as the maximum value of the subinterval sizes tends to zero. Numerical simulations show that high-precision eigenmodes may be obtained by the Müller's method with suitable initial values.
Eigenmode • Helmholtz equation • Optical waveguide • Numerical method • Kummer functions
It is known that the eigenmodes play an important role in optimizing the designs of the microwave engineering for the integrated circuitry [1], microstrip substrates [2], and the integrated optical devices [3,4]. When we compute the wave propagation by use of the eigenmode expansion method, the high-precision propagation constants are needed [5-17]. For the complex and open waveguide with a curved interface, firstly we can construct both the local orthogonal coordinate and the equation transformations [18], and then the original propagation model (Helmholtz equation) is turned to a linear second-order partial differential equation with a flatted interface. The corresponding Sturm-Liouville (S-L) problem is represented as 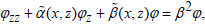 where the variable x is a given value and β is a propagation constant. That is, β2 is known as the eigenvalue λ . Secondly, the open domain is truncated by the perfectly matched layer (PML) [19], or by a coordinate stretching transformation [20,21]. Then, the corresponding S-L problem is changed as
where the variable x is a given value and β is a propagation constant. That is, β2 is known as the eigenvalue λ . Secondly, the open domain is truncated by the perfectly matched layer (PML) [19], or by a coordinate stretching transformation [20,21]. Then, the corresponding S-L problem is changed as 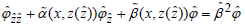 with the interface and the boundary conditions (the domain is bounded), where
with the interface and the boundary conditions (the domain is bounded), where 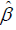 is an approximate value of β . When the transverse variable
is an approximate value of β . When the transverse variable 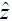 is discretized, there is a discrete set of eigenmodes, which is composed of a finite number of perturbed propagating modes, an infinite sequence of perturbed leaky modes and an infinite number of Berenger modes. Some numerical methods, such as the finite element method (FEM) [22-25], the finite difference method (FDM) [26], the multidomain pseudospectral method [27-29], and the B-spline modal method [30], approximately turn the original S-L problem to a matrix eigenvalue problem. However, we still hardly obtain high-precision eigenvalues, because these methods will produce large and complex matrices causing the difficulties in numerical implementation. For this reason, a different kind of treatment has been proposed, that is, turning the S-L problem to a root-finding problem of a nonlinear dispersion equation, where the roots of the equation are the eigenvalues or the propagation constants. There are some efficient methods to treat slab waveguides [31-33] and rib waveguides [34]. For the varying refractive index’s waveguides terminated by the PMLs, the corresponding S-L problem is expressed as
is discretized, there is a discrete set of eigenmodes, which is composed of a finite number of perturbed propagating modes, an infinite sequence of perturbed leaky modes and an infinite number of Berenger modes. Some numerical methods, such as the finite element method (FEM) [22-25], the finite difference method (FDM) [26], the multidomain pseudospectral method [27-29], and the B-spline modal method [30], approximately turn the original S-L problem to a matrix eigenvalue problem. However, we still hardly obtain high-precision eigenvalues, because these methods will produce large and complex matrices causing the difficulties in numerical implementation. For this reason, a different kind of treatment has been proposed, that is, turning the S-L problem to a root-finding problem of a nonlinear dispersion equation, where the roots of the equation are the eigenvalues or the propagation constants. There are some efficient methods to treat slab waveguides [31-33] and rib waveguides [34]. For the varying refractive index’s waveguides terminated by the PMLs, the corresponding S-L problem is expressed as 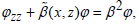 and there are some approximate dispersion equations, which are established by the Wentzel-Kramers-Brillouin (WKB) method [35] and the differential transfer matrix method [36-40]. Yet, these methods cannot guarantee the approximation accuracy of the propagation constants. Although an exact dispersion equation for the waveguide with varying refractive-index profile has been constructed [41], it involves the derivatives of the refractive-index function and highly oscillatory integrals leading to the difficulties in numerical computation. Recently, we give efficient approximations of dispersion relations for the varying refractiveindex waveguides with the two flat interfaces, where the waveguides are open on both sides and terminated by two PMLs, and whose S-L problem is the simple form:
and there are some approximate dispersion equations, which are established by the Wentzel-Kramers-Brillouin (WKB) method [35] and the differential transfer matrix method [36-40]. Yet, these methods cannot guarantee the approximation accuracy of the propagation constants. Although an exact dispersion equation for the waveguide with varying refractive-index profile has been constructed [41], it involves the derivatives of the refractive-index function and highly oscillatory integrals leading to the difficulties in numerical computation. Recently, we give efficient approximations of dispersion relations for the varying refractiveindex waveguides with the two flat interfaces, where the waveguides are open on both sides and terminated by two PMLs, and whose S-L problem is the simple form: 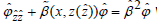 with the interface and the boundary conditions [42]. In this paper, we extend our previous works [42] to the ones for a class of complex waveguides. Namely, the S-L problems are extended to
with the interface and the boundary conditions [42]. In this paper, we extend our previous works [42] to the ones for a class of complex waveguides. Namely, the S-L problems are extended to 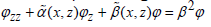 with the interface and the boundary conditions, where the domain is open on one side. For simplicity, we only develop a solver of computing the transverse electric (TE) eigenmodes for the waveguides, which are terminated by the PML along one transverse direction. The rest of this paper is organized as follows. In Section 2, a modified S-L problem (dispersion equation) is introduced when a PML is used, and a solver for the dispersion equations for the TE case is constructed, where the coefficient functions are approximated by the piecewise polynomials of degree two, and the approximate eigenfunctions are expressed analytically by the Kummer functions. In Section 3, the numerical simulations for the TE case are given. Finally, the conclusions are presented in Section 4.
with the interface and the boundary conditions, where the domain is open on one side. For simplicity, we only develop a solver of computing the transverse electric (TE) eigenmodes for the waveguides, which are terminated by the PML along one transverse direction. The rest of this paper is organized as follows. In Section 2, a modified S-L problem (dispersion equation) is introduced when a PML is used, and a solver for the dispersion equations for the TE case is constructed, where the coefficient functions are approximated by the piecewise polynomials of degree two, and the approximate eigenfunctions are expressed analytically by the Kummer functions. In Section 3, the numerical simulations for the TE case are given. Finally, the conclusions are presented in Section 4.
Now, we start from the following equation, which can be obtained by transforming the Helmholtz equation as mentioned above:
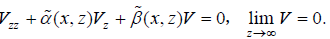 (1)
(1)
When the eigenmode expansion method is used to solve the Eq. (1), the S-L problem of the operator 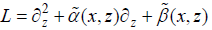 must be considered [43], where x is a given value.
must be considered [43], where x is a given value.
For a dual-layer planar waveguide with the transverse variable z shown in Figures 1 & 2, we consider the S-L problem of the operator L (dispersion equation) as follows:
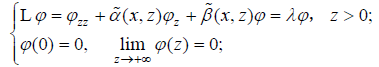 (2)
(2)
where 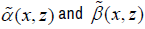 can be regarded as the functions only related with variable z since x is a given value λ is an eigenvalue of the operator L , Ï? is an eigenfunction corresponding the eigenvalue λ , λ = β2 and β is called the propagation constant.
can be regarded as the functions only related with variable z since x is a given value λ is an eigenvalue of the operator L , Ï? is an eigenfunction corresponding the eigenvalue λ , λ = β2 and β is called the propagation constant.
By the feature of the optical waveguides, we assume that 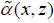 and
and 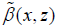 are constants as the variable z is large enough. Namely, there is a d making
are constants as the variable z is large enough. Namely, there is a d making 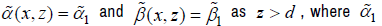 and
and 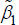 are two constants. So, when z > d , the dispersion equation can be simply written as follows:
are two constants. So, when z > d , the dispersion equation can be simply written as follows:
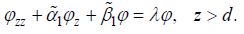 (3)
(3)
In order to numerically solve Eq.(2), we must truncate the open domain to the finite one. Thus, we choose a PML to truncate the open domain, that is, making a complex coordinate stretching transform:
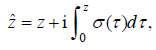 (4)
(4)
where σ(τ) = 0 for 0 ≤ z ≤ H , otherwise  ; here
; here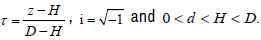
Then, Eq.(2) is approximately turned as the following form:
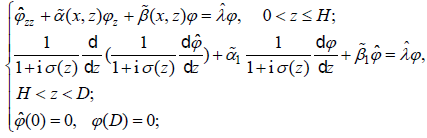 (5)
(5)
where 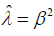 .
.
Case 1: when 0 ≤ z ≤ H , we make the transformation 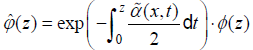 . Then, the equation
. Then, the equation
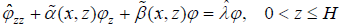 (6)
(6)
can be transformed to the following form:
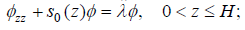 (7)
(7)
where 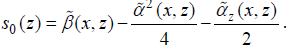
Case 2: when H < z ≤ D , we make the other transformation 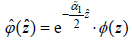 . Then, the equation becomes
. Then, the equation becomes
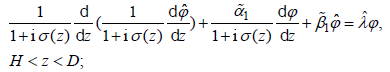 (8)
(8)
that is,
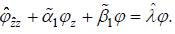 (9)
(9)
It can be transformed to the following form:
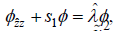 (10)
(10)
where 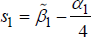 is a constant.
is a constant.
Thus, the original eigenvalue problem of the operator L is approximated by
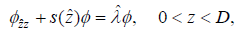 (11)
(11)
where 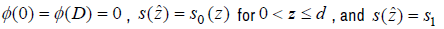 for
for 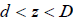
Remark 1: 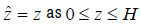
For the reason that it is a differential equation with variable coefficients in [0, d] , we first divide the interval [0, d] into k subintervals with 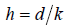 . Then the subintervals are denoted by
. Then the subintervals are denoted by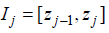 related to
related to 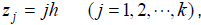 and the function s0 (z) is interpolated by a polynomial of degree two, and yj (z) is the approximation of the φ (z) as z∈ Ij . Thus, the form of approximated equation is
and the function s0 (z) is interpolated by a polynomial of degree two, and yj (z) is the approximation of the φ (z) as z∈ Ij . Thus, the form of approximated equation is
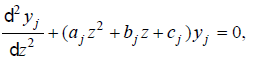 (12)
(12)
where the coefficients of approximated equation are given by
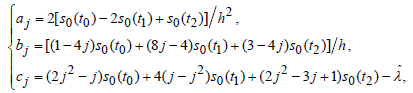 (13)
(13)
here 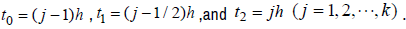
Eq.(12) can be changed to the form of the confluent hypergeometric equation, and a pair of linearly independent solutions {mj (z), nj (z)} as z∈ Ij are given by the Kummer functions. Then the approximated solution of φ as z∈ Ij can be expressed in the following form 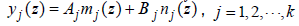
Suppose ωj (z) is the approximation of 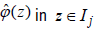 , we have
, we have
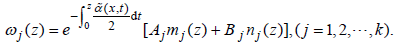 (14)
(14)
Since s1 is constant for d < z < D , the results of field 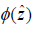 satisfy
satisfy 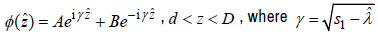
Set z0 = 0 and zk+1 = D , then two linearly independent solutions are shown on [zk , zk+1] as follows:
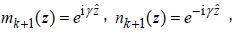 (15)
(15)
with the boundary conditions φ (0) = 0 and 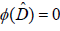 . Therefore, the approximated solutions of φ at z0 = 0 and φ at zk+1 = D should be defined as y1(0) = 0 and yk+1(D) = 0 , respectively
. Therefore, the approximated solutions of φ at z0 = 0 and φ at zk+1 = D should be defined as y1(0) = 0 and yk+1(D) = 0 , respectively
To obtain the constants of Aj and Bj ( j = 1, 2,..., k) we require the solutions ωj(z) of field 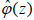 and their first order derivatives are continuous at zj. Thus, the interface conditions at zj ( j =1,2,...,k) are
and their first order derivatives are continuous at zj. Thus, the interface conditions at zj ( j =1,2,...,k) are
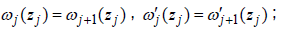 (16)
(16)
that is,
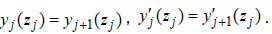 (17)
(17)
According to these conditions, a linear system of Aj and Bj ( j =1,2,...,k) can be obtained.
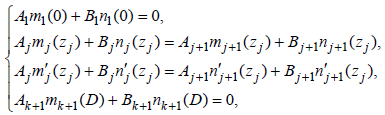 (18)
(18)
here ( j =1,2,...,k) . In order to simplify these equations, let Rj=Bj/Aj (j=1,2,...k), the dispersion relations of 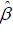 are
are
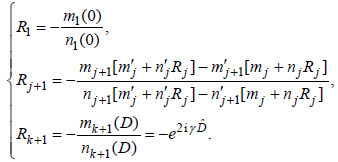 (19)
(19)
Specially, when j = k ,
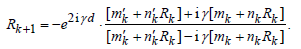 (20)
(20)
The evaluation on Rk+1 depends on R1 recursively. Furthermore, Rk+1 is determined by 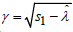 . Hence, the dispersion relation with respect to
. Hence, the dispersion relation with respect to 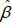 is as follow:
is as follow:
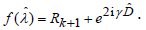 (21)
(21)
Special Case: when 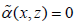 , the S-L problem of the operator L becomes
, the S-L problem of the operator L becomes
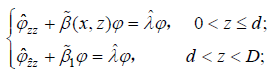 (22)
(22)
where 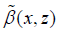 depends only on z , and
depends only on z , and 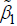 is a constant. Moreover, the top and bottom boundary conditions are
is a constant. Moreover, the top and bottom boundary conditions are 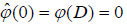 . Applying a polynomial of degree two to interpolate the function
. Applying a polynomial of degree two to interpolate the function 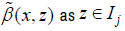 , then we get the approximated equation
, then we get the approximated equation
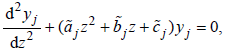 (23)
(23)
where
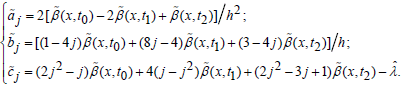 (24)
(24)
Referring to the Kummer functions, eventually, we derive the dispersion relations as follows
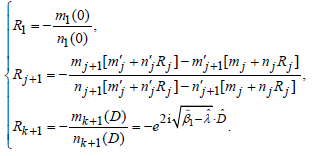 (25)
(25)
Asymptotic solutions for the TE case: for the Berenger modes in a dual-layer optical waveguide terminated by a PML, 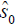 is the average value of s0 (z) at the 17 points distributing equally within the interval [0, d] . We can obtain the following formula [44]:
is the average value of s0 (z) at the 17 points distributing equally within the interval [0, d] . We can obtain the following formula [44]:
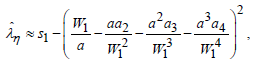 (26)
(26)
where Im(W1) > 0 ,η is an integer, and
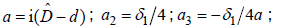
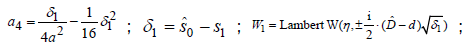
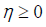 except
except 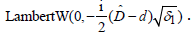
And asymptotic solutions of leaky modes are also obtained as follow [44]:
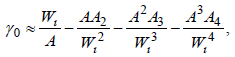 (27)
(27)
where
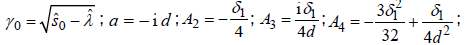
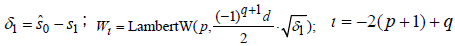 ; for
; for 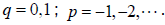
At last, we find the roots of the equation 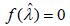 by the Müller’s method with suitable initial values, which are taken by the asymptotic solutions.
by the Müller’s method with suitable initial values, which are taken by the asymptotic solutions.
The theory of this paper has been implemented and tested on a number of examples. For simplicity, we still denote β as 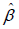 in the following statements.
in the following statements.
For example, let C =16 , d = 0.8 , H =1.6 , D = 1.7 , s1 =1.452 ,
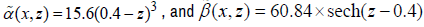 .
.
Therefore, s0(z) = 60.84[sech(z − 0.4) − (0.4 − z)6 + 3(0.4 − z)2/7.8] for 0 < z ≤ d .
The propagation constants β of propagating modes satisfy min(s0(z)) < β2 < max(s0(z)) for 0 < z ≤ d . Thus, the propagation constants of propagating modes, leaky modes and Berenger modes are shown in Tables 1, 2 and 3, respectively. In Table 1, β1 , β2 and β3 are taken as the initial values. In Tables 2 and 3, β1 , β2 and β3 are represented as the iterative values as k = 16, 32 and 64, respectively.
| β1 | β2 | β3 | Approximate Solution β |
|---|---|---|---|
| 7.740 7.755 7.770 7.785 |
7.745 7.760 7.775 7.790 |
7.750 7.765 7.780 7.795 |
7.02573-0.00000i 7.02573-0.00000i 7.02573-0.00000i 7.02573-0.00000i |
| t | β1for k=16 | β2for k=32 | β3for k=16 |
|---|---|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
0.83852+ 5.42434i 1.52393+11.41193i 1.92469+15.63788i 2.33529+19.97154i 2.48289+24.20780i 2.63137+28.30444i 2.77607+32.36134i 2.90682+36.39285i 3.02505+40.40465i 3.13316+44.40159i 3.23285+48.38733i 3.32531+52.36441i 3.41152+56.33462i 3.49226+60.29931i 3.56816+64.25948i 3.63978+68.21591i 3.70756+72.16920i 3.77190+76.11984i 3.83312+80.06821i 3.89152+84.01462i |
0.83852+ 5.42434i 1.52393+11.41192i 1.92468+15.63788i 2.33529+19.97154i 2.48289+24.20780i 2.63137+28.30444i 2.77607+32.36133i 2.90682+36.39285i 3.02504+40.40464i 3.13316+44.40159i 3.23284+48.38733i 3.32531+52.36440i 3.41151+56.33462i 3.49224+60.29931i 3.56815+64.25949i 3.63977+68.21592i 3.70755+72.16921i 3.77190+76.11984i 3.83312+80.06821i 3.89152+84.01462i |
0.83852+ 5.42434i 1.52393+11.41192i 1.92468+15.63788i 2.33529+19.97154i 2.48289+24.20780i 2.63137+28.30444i 2.77607+32.36133i 2.90682+36.39285i 3.02504+40.40464i 3.13316+44.40159i 3.23284+48.38733i 3.32531+52.36440i 3.41151+56.33462i 3.49224+60.29931i 3.56815+64.25949i 3.63977+68.21592i 3.70755+72.16921i 3.77190+76.11985i 3.83312+80.06821i 3.89152+84.01462i |
| η | β1for k=16 | β2for k=32 | β3for k=16 |
|---|---|---|---|
| 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 |
1.74842+ 9.71020i 2.42335+13.41599i 2.96306+16.91230i 3.51505+20.14151i 4.31788+23.37743i 5.09828+26.69102i 5.86661+29.99240i 6.64466+33.27954i 7.43504+36.56089i 8.23428+39.83971i 9.04015+43.11623i 9.85166+46.39052i 10.66815+49.66286i 11.48902+52.93352i 12.31375+56.20274i 13.14192+59.47070i 13.97316+62.73752i 14.80716+66.00335i 15.64367+69.26828i 16.48245+72.53239i |
1.74842+9.710198i 2.42335+13.41599i 2.96306+16.91230i 3.51505+20.14151i 4.31788+23.37743i 5.09828+26.69102i 5.86661+29.99241i 6.64466+33.27954i 7.43504+36.56089i 8.23429+39.83971i 9.04016+43.11623i 9.85167+46.39052i 10.66815+49.66286i 11.48902+52.93352i 12.31376+56.20274i 13.14193+59.47069i 13.97317+62.73752i 14.80717+66.00335i 15.64367+69.26827i 16.48245+72.53239i |
1.74842+9.710198i 2.42335+13.41599i 2.96306+16.91230i 3.51505+20.14151i 4.31788+23.37743i 5.09828+26.69102i 5.86661+29.99241i 6.64466+33.27954i 7.43504+36.56089i 8.23429+39.83971i 9.04016+43.11623i 9.85167+46.39052i 10.66816+49.66286i 11.48902+52.93352i 12.31376+56.20274i 13.14193+59.47070i 13.97317+62.73752i 14.80717+66.00335i 15.64367+69.26827i 16.48245+72.53239i |
To compute the eigenmodes of the complex optical waveguide which is open on one side, based on our previous methods, the second-order linear differential equation in standard form of the corresponding S-L problem has been reduced to the equation without the first derivative term. Then, a PML is used to terminate the open waveguide. Also, the coefficient function of the simplified S-L problem is approximated by a piecewise polynomial of degree two. Since the solutions of the approximated equation in each layer are analytically expressed by the Kummer functions, the approximate dispersion equation is established to the TE case. Apparently, the approximate solutions will converge to the exact ones as the number k of subintervals tends to infinity, or equivalently the step size tends to zero. In the numerical example, we find out the roots of the dispersion equation by the Müller’s method, where three different asymptotic solutions of slab waveguides play the roles of initial values. Numerical simulations show that the iteration converges fast and high-precision values for propagation constants may be obtained only if a suitable root-finding method is adopted and some good initial values are given. Thus, further research will be performed in future.
When a ≠ 0 , let’s begin to consider the second order differential equation as follow
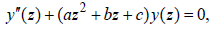 (28)
(28)
by the change of variables 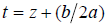 , we have
, we have
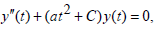 (29)
(29)
where C = c −[b2(4a)] .
Further change of variables
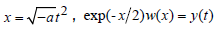 (30)
(30)
leads to
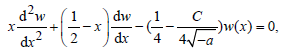 (31)
(31)
which is in the form of the confluent hypergeometric equation
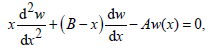 (32)
(32)
with 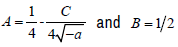 . Two linearly independent solutions are given by the Kummer functions M(A, B, x) and U(A, B, x) .However, U(A, B, x) has a branch point x = 0 , Hence, two linearly independent solutions of Eq. (28) are given by
. Two linearly independent solutions are given by the Kummer functions M(A, B, x) and U(A, B, x) .However, U(A, B, x) has a branch point x = 0 , Hence, two linearly independent solutions of Eq. (28) are given by
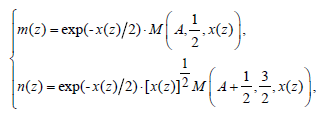 (33)
(33)
where
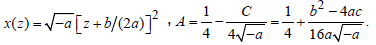
Recall the following differential formulas for the Kummer function:
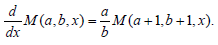 (34)
(34)
The derivatives of m(z) and n(z) can be expressed as
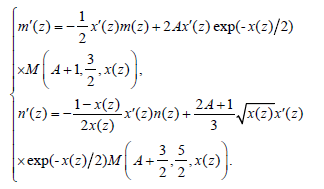 (35)
(35)
Special Case: when a=0, and b ≠ 0 , Eq.(28) becomes
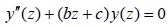 (36)
(36)
and two linearly independent solutions are given by the Airy functions
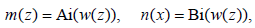 (37)
(37)
where 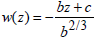 Therefore,
Therefore,
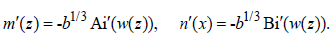 (38)
(38)
The Airy functions and their derivatives can be evaluated in Matlab as.
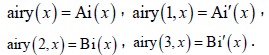 (39)
(39)
When a = b = 0 , Eq.(28) becomes
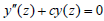 (40)
(40)
which has two linearly indecent solutions
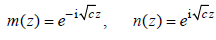
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report