Research Article - (2022) Volume 11, Issue 6
Received: 02-Jun-2022, Manuscript No. JACM-21-002;
Editor assigned: 04-Jun-2020, Pre QC No. P-002;
Reviewed: 18-Jun-2020, QC No. Q-002;
Revised: 20-Jun-2022, Manuscript No. R-002;
Published:
27-Jun-2022
, DOI: 10.37421/2168-9679.22.11.479
Citation: El-Sobky, Bothina, Gehan Ashry and Yousria Abo-Elnaga. "An Interior-Point Method for Nonlinear Constrained Optimization Problem with Trust-Region Mechanism." J Comput App Math. 11(2022):479.
Copyright: © 2022 Ashry G, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
We introduced an algorithm to solve a Non Linear Constrained Optimization (NLCO) problem in this paper. This algorithm follows Das’s idea of Newton’s interiorpoint method that uses a diagonal matrix of Coleman and Li for NLCO problems. A Trust-Region (T-R) mechanism is used to globalize the algorithm. This algorithm follows Byrd and Omojokun’s idea of step decomposition. It is a successful idea to overcome the difficulty of having an infeasible quadratic T-R sub problem and converts the quadratic T-R sub problem into two unconstrained T-R sub problems.
A global convergence theory of the algorithm is studied under five standard assumptions. This algorithm is different and maybe simpler than similar ideas such that the global convergence theory is not depending on the linear independence assumption on the gradients of the constraints.
Some numerical tests are stated to indicate that the algorithm performs effectively and efficiently in pursuance.
Nonlinear constrained optimization• Newton method• Interior-point method• Trust-Region mechanism• Coleman-Li matrix• Global convergence
We described and analyzed an interior point algorithm in this paper to solve the following NLCO problem,
minimize f (x) (1.1)
subject to g (x)=0,
a ≤ x ≤ b,
where,
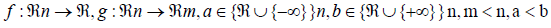
Motivated by the impressive computational performance of the primal dual interior-point method for linear programming, authors in using the Coleman- Li scaling matrix, proposed a primal interior-point algorithm for solving nonlinear programming problems having a special structure [1].
In particular, their algorithm is designed for solving a special nonlinear programming where the vector of primal variables x is naturally divided into a vector of state variables and a vector of control variables. They proved several global and local convergence results for their algorithm. In this paper, we use the Coleman-Li scaling matrix to propose the interior-point Trust- Region algorithm for solving nonlinear programming Problem (1.1). The Coleman-Li scaling matrix was first introduced for unconstrained optimization problem and used for equality constrained optimization problem [2].
Newton’s interior-point method which was suggested by and used with is used in the proposed algorithm. It converges quadratically to a stationary point under reasonable assumptions but the starting point must be sufficiently closed to the stationary point in order to guarantee convergence. That is, it may not converge at all if the starting point is far away from the solution.
A Trust-Region (T-R) mechanism is a well-accepted mechanism in NLCO problem to ensure the global convergence. One of the advantages of T-R mechanism is that it does not require the objective function of the model to be convex. Also, it does not seek the Hessian of the objective function must positive definite. However, in traditional T-R mechanism, after solving T-R sub problem, we need to use some criterion to check if the trial step is acceptable. If not, the T-R sub problem must be resolved by a reduced T-R radius. Similar ideas can be found. Our balance idea mainly differs from these algorithms in the way of computing trial steps, the way of updating the penalty parameter, the way of updating the Hessian matrix, and the global convergence theory which is proved without the assumption of linear independence on the gradients of the equality constraints. The mechanism of our method seems simpler than these methods [3].
If the Trust-Region constraint is simply added to the sequential quadratic sub problem of the equality constrained optimization problem, the resulting Trust-Region sub problem may be infeasible, because there may be no intersecting points between the Trust-Region constraint and the hyperplane of the linearized constraints. Even if they intersect, there is no guarantee that this will remain true if the Trust-Region radius is decreased.
Byrd-Omojokuns idea is a successful method to overcome the difficulty of having an infeasible T-R sub problem. This method was suggested by, and used. In this method, the trial step is decomposed into two orthogonal components; the tangential component and the normal component. Each component is computed by solving a Trust-Region sub problem. One of the advantages of this method, the two sub problems is similar to the Trust- Region sub problem for the unconstrained case. Under necessary assumptions, a global convergence theory for the proposed interior-point Trust- Region algorithm is introduced [4].
Global convergence results of many T-R algorithms were proved under the assumption of linear independence on the gradients of the equality constraints and other mild assumption. In this paper, our global convergence theory is not depending on the assumption of linear independence on the gradients of the equality constraints. So, our global convergence theory is generic that it holds for many T-R algorithms which are used the augmented Lagrangian as a merit function, Hessian estimates, and bounded Lagrange multiplier [5].
In this trajectory, the suggested T-R algorithm always output a new point, and avoids possibly two sub problems are solved many times, so that the performance of the algorithm is improved. A global convergence theory for the proposed algorithm is presented under mild conditions. In particular, regularity condition of the constraints is not assumed. Moreover, numerical experiments display that the suggested algorithm performs effectively and efficiently in pursuance [6].
The balance of this paper is organized as follows. In the next section, Newton’s interior-point method is introduced. We describe the design of the algorithm in detail while the global convergence. We report preliminary numerical results. Finally, some further remark is given [7].
We use ll.ll to denote the Euclidean norm ll.ll2. Subscript k refers to iteration indices and superscript i is the ith component of a vector. For example,
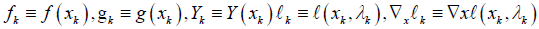 ,
,
and so on to denote the function value at a particular point [8].
Newton’s interior-point idea for NLCO problems
In this section, we introduce and analyze Newton’s interior-point idea for NLCO problems. Let
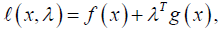 (2.1)
(2.1)
be a Lagrangian function associated with Problem (1.1) without the bounded constrain a ≤ x ≤ b. Let
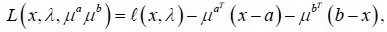 (2.2)
(2.2)
be a Lagrangian function associated with Problem (1.1). The vectors λ, μa, and μb represent the Lagrange multiplier vectors associated with the constraints g(x)=0, 0 ≤ (x−a), and 0 ≤ (b−x) respectively. Let F̃̃̃ ={x:a ≤ x≤ b} and int (F)={x : a < x < b}.
The first-order necessary conditions for the point x∗ ∈ F˜ to be a local minimizer of Problem (1.1) are the existence of multipliers λ∗ ∈ℜm, μa ∈ ℜn , and μb ∈ ℜn , such that (x∗, λ∗, μa, μb ) satisfies
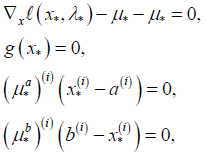
The above four equations indicates (2.3) (2.4) (2.5) (2.6)
for all i corresponding to x(i) with finite bound and
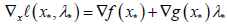
Let Y (x) be a diagonal matrix whose diagonal elements are defined as follows
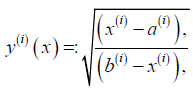
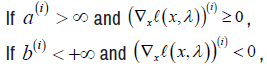 (2.7)
(2.7)
This matrix was first introduced in for unconstrained optimization problem and was used by for NLCO problems. Using the matrix Y (x), the conditions (2.3)-(2.6) are equivalent to the following conditions
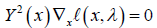 (2.8)
(2.8)
g (x) = 0 (2.9)
Such that 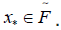 Let Let ψ(x) be a vector whose elements are defined by
Let Let ψ(x) be a vector whose elements are defined by
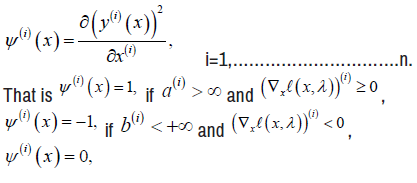 (2.10)
(2.10)
Applying Newton’s method on the nonlinear system (2.8)-(2.9), then we have
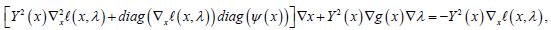
It is easy to see that the step generated by the above system coincides with the solution of the following quadratic programming sub problem
Minimize 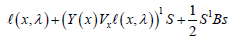 (2.13)
(2.13)
Subject to 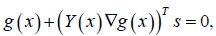
Where 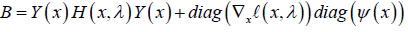
such that H(x,λ) represents the Hessian of the Lagrangian function (2.1) or an approximation to it.
If T-R constraint is simply added to quadratic programming sub problem (2.13), the resulting problem will take the form where δk>0 is the radius of the Trust-Region [8]. The above T-R subproblem may be infeasible because there may be no intersecting points between T-R constraint and the hyperplane of the linearized constraints. Even if they intersect, there is no guarantee that this will remain true if T-R radius is decreased.
To overcome the difficulty of having an infeasible T-R sub problem we will use Byrd-Omojokuns method. In this method, the trial step is decomposed into a normal step and a tangential step.
Description of (NIPTR) algorithm
We introduce the main algorithm in this section. We clarify the main framework of the Newton’s Interior-Point Trust-Region (NIPTR) algorithm to solve Problem (1.1) [9].
How to compute a step Sk
For sub problem (2.13), we follow Byrd-Omojokuns mechanism to compute the trial step Sk. In this mechanism, the step Sk is decomposed into the normal step Sn and the tangential step St=ZkSt, where Zk is a matrix whose columns form a basis for the null space of (Yk∇gk) T.
To obtain the normal step, we solve the following T-R sub problem
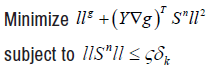
for some 0 < ϛ< 1. Our way of solving the above T-R sub problem is to approximate its solution using the dogleg mechanism. More details about dogleg mechanism [10].
How to test the step τθYksk and update δk
Choose 0<γ1<γ2<1, 0<α1<1<α2, and δmin ≤ δ0 ≤ δmax.
Reduce the Trust-Region radius by setting δk=α1llSkll.
accept the step: xk=xk+τθYkSk.
Set δk+1=max (δk, δmin).
Set δk+1=min {δmax, max {δmin, α2δk}}.
Global convergence analysis
To establish the global convergence theory for NIPTR algorithm, we need the following assumptions.
A necessary assumption:
Let {xk} be the sequence of points generated by NIPTR algorithm.
The following assumptions are necessary to prove the global convergence theory of NIPTR algorithm.
There is a convex set ΩRn and containing {xk}.
The functions f (x), g (x) C2 for all xΩ.
All of f (x), ∇f (x), ∇2f (x), g (x), ∇g (x), ∇2gi (x) for i=1..., m, and (Yk∇gk) {(Yk∇gk)T (Yk∇gk)}−1 are uniformly bounded in Ω.
The sequence {λk} is bounded.
The sequence of approximated Hessian matrices {Hk} is bounded.
An instantaneous results of the above necessary assumptions is that there exists a constant 0<b1, such that, Zk Bk ≤ b1, Zk BkZk ≤ b1.
Observe that the above assumptions do not comprise the assumption of linear independence on the gradients of the scaled equality constraints, a commonly used assumption by many authors. So, we may have other kinds of stationary points which are presented in the following definitions [11].
Feasible mayer-bliss point
A point xF is called a Feasible Mayer-Bliss (FMB) point of Problem (1.1), if there exist a Lagrange multiplier vector λRm and a constant νR not all zeros such that the point (x, ν, λ) satisfies the following conditions:
ν*Y (x*)∇f (x*)+Y (x*)∇g (x*) λ*=0,
g (x*)=0.
If ν*=0, the FMB conditions are coincide with the following conditions
Y (x)∇f (x)+Y (x )∇g(x ) λ*=0
g (x*)=0,
and in this case, these conditions are called a Karush-Kuhn-Tucker (KKT) conditions of Problem (1.1) and the point (x , 1, λ* ) is called KKT point.
Infeasible mayer-bliss point
A point x* ∈ F is called an Infeasible Mayer-Bliss (IFMB) point of Problem (1.1), if there exist a Lagrange multiplier vector λ* Rm and a constant ν* R not all zeros such that the point (x*, ν*, λ*) satisfies the following conditions:
ν*Y (x*)∇f (x*)+Y (x*)∇g (x*) λ*= 0
Y (x*) ∇g(x*)g(x*)=0
If ν*= 0, then IFMB conditions are coincide with the following conditions
Y (x )∇f (x ) + Y (x )∇g(x ) λ*=0
Y (x*)∇g(x*)g(x*) = 0,
and in this case, conditions are called an infeasible KKT conditions and the point (x*, 1, λ*) is ν* called an infeasible KKT point.
Let {kj} be any subsequence of iteration sequence that satisfies FMB conditions that are not KKT conditions. From Definition 4.1, we notice that, for all k ∈ {kj} the corresponding sequence of smallest singular values of the matrices Yk∇gk is not bounded away from zero.
Throughout the rest of the paper, we use {Ykj ∇g kj} to denote the sequence of smallest singular values of Yk∇gk for all k ∈{kj}.
If ν*=0, then IFMB conditions are coincide with the following conditions
Y (x*) ∇f (x*)+Y (x*) ∇ g (x ) λ*=0,
Y (x*) ∇g (x*) g (x*)=0,
Let {kj} be any subsequence of iteration sequence that satisfies FMB conditions that are not KKT conditions. For all k ∈ {kj} the corresponding sequence of smallest singular values of the matrices Yk∇gk is not bounded away from zero.
The algorithm NIPTR is performed on some of test problems listed for the same starting points to show effectiveness of algorithm NIPTR. For comparison, we have included the corresponding results of NIPTR algorithm against the corresponding numerical results. This is summarized in Table 1. In this table, Niter refers to the number of iterations. For all problems, these algorithms achieved the same optimal solution at the same starting points.
| Problem name | Method in Niter | (NIPTR) algorithm Niter | Problem name | Method in Niter | (NIPTR) algorithm Niter |
|---|---|---|---|---|---|
| hs006 | 7 | 3 | hs042 | 3 | 3 |
| hs007 | 27 | 14 | hs043 | 7 | 6 |
| hs008 | 5 | 4 | hs044 | 6 | 4 |
| hs009 | 6 | 14 | hs045 | 17 | 8 |
| hs010 | 11 | 9 | hs047 | 16 | 5 |
| hs011 | 6 | 7 | hs048 | 2 | 4 |
| hs012 | 7 | 5 | hs049 | 15 | 9 |
| hs013 | 15 | 10 | hs050 | 8 | 9 |
| hs014 | 6 | 8 | hs051 | 2 | 8 |
| hs015 | 9 | 9 | hs052 | 2 | 7 |
| hs016 | 11 | 10 | hs053 | 4 | 4 |
| hs017 | 9 | 10 | hs055 | 4 | 6 |
| hs018 | 9 | 8 | hs056 | 6 | 4 |
| hs019 | 39 | 10 | hs060 | 7 | 6 |
| hs020 | 4 | 5 | hs061 | 6 | 8 |
| hs021 | 5 | 5 | hs062 | 6 | 6 |
| hs022 | 6 | 6 | hs063 | 17 | 7 |
| hs023 | 7 | 6 | hs064 | 14 | 10 |
| hs024 | 8 | 9 | hs065 | 9 | 7 |
| hs026 | 17 | 12 | hs066 | 9 | 6 |
| hs027 | 16 | 5 | hs067 | 13 | 6 |
| hs028 | 2 | 4 | hs071 | 8 | 10 |
| hs029 | 7 | 8 | hs072 | 16 | 18 |
| hs031 | 4 | 3 | hs073 | 7 | 7 |
| hs032 | 9 | 7 | hs076 | 6 | 5 |
| hs033 | 7 | 7 | hs077 | 11 | 9 |
| hs034 | 9 | 8 | hs078 | 4 | 4 |
| hs035 | 8 | 9 | hs079 | 4 | 6 |
| hs036 | 6 | 7 | hs080 | 7 | 7 |
| hs037 | 6 | 7 | hs081 | 7 | 6 |
| hs039 | 17 | 12 | hs093 | 5 | 4 |
We use the logarithmic performance profiles which proposed by and our profiles are based on Niter. We observe that the NIPTR algorithm is quite well compared with algorithm. The performance profile in terms of Niter is given in Figure 1 and show a distinctive for the algorithm NIPTR over the algorithm.
We described the Newton’s interior-point Trust-Region NIPTR to solve NLCO problem. In NIPTR algorithm, Newtons interior-point method is used together with the diagonal matrix of Coleman and Li for NLCO problems. A Trust-Region (T-R) globalization mechanism is added to our algorithm to insure global convergence. A global convergence analysis for NIPTR algorithm is presented under five assumptions and without the regularity assumption, a commonly used assumption by many researchers.
Preliminary numerical experiment on the algorithm is presented. The performance of the algorithm is reported. The numerical results show that our approach is of value and merit further investigation. For future work, there are many question should be answered.
Improving the proposed algorithm to be capable for treating large scale bound constrained optimization problem with equality and inequality constraints and non differentiation case.
We have to implement the proposed algorithm on real life. How to
The author would like to thank the anonymous referees for their valuable comments and suggestions which have helped to greatly improve this paper.
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report