Analysis of Testing the Pricing Efficiency of Options Using Greeks and BSM in Nifty Index

D. Subalakshmi^* and K. Prabhakar Rajkumar
^*Correspondence: D. Subalakshmi, Department of Commerce, Periyar University, Salem, India, Email:

Keywords

Call • Put Option • Option Greeks • BSOPM • Option moneyness

Introduction

Since ancient times, "contracts" similar to "options" have been in practice. Thales of miletus, an ancient Greek mathematician and philosopher was the first apparent "option" buyer [1]. On a certain occasion, Thales assumed that production of "olives" would be higher than expected, and thus during the off-season, he acquired the right to keep hold of some olive presses for the following olives harvesting season. When the final climax approached, the olive harvest was more enormous than expected; he executed his right of options and took hold of the presses, rented out a much higher price than he paid for his 'option'. Derivatives are financial contracts that attain value from something else, known as underlying securities [2]. As we generally know, underlying securities may be stocks, currency, commodities or bonds, etc. There is a general assumption about the relationship between the prices between underlying assets and futures and those arbitrageurs maintain solely [3]. On a smooth sailing of this relationship, investors can fix these markets as ideal substitutes and conclude that trading in these markets is driven by expediency and the price tag. Unfortunately, many studies have so far proven the presence of considerable deviation between futures prices and consequent theoretical values, resulting in "carry cost".

In the Indian capital market, futures and options are commonly traded derivatives and NSE enjoys a monopoly in derivatives trading, holding the upper hand in dealing with impacts on risk management. NSE introduced trading in the Nifty 50 index option in June 2001. Since then, NSE has provided index option contracts on 9 major indices, among them Nifty 50, Bank Nifty, Nifty Midcap 50, and Nifty IT more frequently trade index options [4]. In 1973, Black, Myron Scholes, and Robert Merton developed a theoretical option pricing model that fascinated traders and popularly became to be known as the "Black-Scholes model" BSM. The practice of quoting theoretical stock index futures prices has grown widespread. Nifty futures are traded below the Nifty spot value in commodity pricing strategy, and quoting futures prices below spot prices is uncommon. Even though futures prices are lower than spot prices, physical commodity owners will soon be unable to sell their commodities at the current higher prices and profit from the price differential due to specific restrictions [5]. In the case of farm produce, before harvest spot prices may increase due to assuming shortages of supply, but ultimately the prices are reduced after reaping when fresh supplies are surplus. As a result, discrepancies in the real price of options and the prices anticipated using the formula may arise while implementing the option pricing formula [6].

Fischer Black, the co-author of the famous Black and Scholes model, attempted to address the problem of the negative cost of carry in the option pricing model by substituting forward prices for spot prices in 1976. He discovered that, in addition to the inventory carrying cost, a real forward price catches other market irregularities as well [7]. The results of Black's approach helped evaluate options on physical commodities with a common negative Cost of Carry. In this study, we attempted to predict the pricing efficiency of options prices using Greeks and the Black-Scholes formula, compared theoretical values to actual prices in the real-time market and discovered that the Black-Scholes formula produced better results for Nifty options [8].

This pricing model is universally accepted by all investors, though this model could make certain pricing prejudice in the realistic market as it provides an analytical solution for option price along with its sensitivities to risks recognized as option Greeks [9]. The options Greeks have taken for calculation are delta, gamma, theta, vega, and rho, which are sensitive to particular market variables like strike price, underlying value, time to expiry, interest rate, etc. Few researchers have also proved that the intensity of these Greeks has a simultaneous impact on options positions significantly [10]. The success of options trade mainly depends on the direction of market moves and also the Greeks dictate the movement of the option price.

Literature Review

Cornell and French used daily data to investigate the "cost of carry" model in stock index futures pricing and arbitrage opportunities, and discovered that there is mispricing. A lot of research looks into arbitrage trading opportunities and the disparities between theoretical and actual option prices. Arbitrage is predicated on the reality of a frictionless market where traders perform transactions whenever the prices of options and futures contracts stray from their respective fair values. However, there are various barriers to the time-arbitrage process, including operational and regulatory constraints; transaction costs; the risk inherent in the process; margin risk; short-selling restraints; and even more real-time hazards. In his research, Sundaresan discovered that arbitrageurs lose "interest earnings" on the proceeds of short-sale equity when the pricing band goes below the fair price. Lazibat and Bakovic state that price risk is one of the most important and many foreign trade companies face [11]. This can be solved by concentrating on options Greeks, usually considered as foremost factors for speculation, which can successfully be implemented for price risk elimination. Yuh-Dauh and Teng in their research found that risk hedging through option Greeks is less varied from the authentic result, which helps predictions by using various formulas numerically which are unbiased [12]. Xishen and Xiaoke state that the Greek letter measures the sensitivity of an option price, relating to the changes in the value of a given underlying asset's price, value, time, etc. Jelena explores market risk management from the options trader perspective and explains how to describe the risk characteristics of European stock option contracts by applying the Greeks. Kakati experimented with the pricing option contracts for ten Indian stocks using Black-Scholes (BS) model, which is considerably mispriced in many cases. However, it is hard to draw generalized conclusions from research studies since the limitations are restricted to only ten Indian stock option contracts [13]. Saravanan and Pradeep state that the accuracy of the Black-Scholes option pricing model and its relation to market prices also helps in finding whether the stock options are properly priced. Khan et.al found that the credit rate in India is being assessed using the Black-Scholes-Merton model which resulted in an unsolved dispute between liquidity premium and transaction costs of market spreads [14].

Sanjana observed that trading options and option strategies are based on risk factors and can only be predicted using Greeks [15]. Paired sample T-test proves that there is no significant difference between the expected option prices calculated through the Black- Scholes model and the market price of options Panduranga. It is conditional that the model is relevant for cement stocks only. Whereas Nagendra and Venkateswar state that the robustness of the Black-Scholes model in pricing, and stock options in India and that pricing is further improved by incorporating implied volatility in the model [16]. Nilakantan and Shalini in their study observed that the Black-Scholes model is defective notwithstanding its prevalent use in hedging because it predicts continuous hedging and zero transaction cost. The research work of Rajanikanth and Lokanadha explored the price of a European option in the future and its sensitivity through Greek letters and measure the risks using delta, vega, theta, rho, and gamma. Muthusamy and Vivek identified that in most contracts, the option prices calculated are different from the market value of the contract [17]. However, many studies suggest that the BSM model is appropriate for estimating the European option's price, and also it provides an arbitrage opportunity for the financiers in India. Bhardwaj states that the financial market in India is to grow rapidly in the long run, owing to the developments brought in by the Indian government [18]. Even though a derivative contains risk factors, investors have to handle the situation carefully so that they can do wonders. The effectiveness of commonly used Greeks; (Delta, Gamma, Theta, Vega, and Rho) and their significance in managing various types of risks is commonly associated with an option contract was stated by Kumar in his research. Therefore, patrons use the Greeks under the Black-Scholes model framework as a benchmark for appropriately adjusting option positions, enabling them to manage risks [19].

In this empirical paper, the focus is on the Nifty index option and analyzes the impact of each Greek option from the buyer's perspective [20]. This paper also includes the estimated daily Nifty option value (both call and put) and option Greeks, which expired on 25-Nov-18 within the framework of the Black-Scholes option pricing model. For this analysis, four strike prices 10100, 10900, 11100, and 11300 have been selected. Finally, the estimated Greeks value helps in understanding the different dimensions of the risk in a Nifty option position enabling successful management of risks [21].

Objectives of the study

The following objectives are set based on the reviews collected for this paper:

• To estimate the Nifty option price and Greeks is using the Black- Scholes model for each selected strike price.
• To examine the different dimensions of risk involved in Nifty option positions, using Greeks.

Research methodology

Determining the strike price is very important for an options investor since it has a very momentous impact on the profitability of an option position [22]. Working on necessary base calculations to select the optimum strike price is a very necessary step to improvise the chances of accomplishing options trading. The sample of the study covers the daily European call and Put Nifty option price for strike prices 10100, 10900, 11100, and 11300 which expired on 25- Nov-2018. This secondary data is collected from 01-November-2018 to 25-November-2018 from the NSE website. The researcher used Nifty option Greeks and estimates within the Black-Scholes model framework for selected strike prices, using an available online calculator for Black-Scholes option pricing model and option Greeks [23].

The researcher has used the online calculator to estimate the daily implied volatility. As per the Black-Scholes, option pricing model assumptions implied volatility and risk free interest rate remains constant [24]. But in this empirical paper, we consider fluctuation and change in the implied volatility for each day from 1-November-2018 to 25-November-2018. Implied volatility is taken as fluctuating input variables (%), underlying Nifty spot value, and days until expiration; the risk free interest rate is 10% as per the NSE website. The dividend yield is zero since the Nifty option is an index option [25].

Formulae or models used

Black-Scholes option-pricing model: (Dividend yield is zero)

S-Spot price

K-Strike price

σ -Volatility

T-Time till the expiry date

r-Risk-free interest rate

N represents a standard normal distribution with a mean of 0 and a standard deviation of 1, and ln represents the natural logarithm of a number. Natural logarithms are based on the constant e (2.71828182845904) [26].

Option Greeks

Delta (Δ): Delta is the most important of all the options for Greeks. It measures the impact of change in the price underlying (that is, the premium of an option) resulting from a change in the underlying security. A positive value for the call option varies from 0 to 1 and a negative value for the put option varies from-1 to 0.

Gamma (γ): It measures the rate of change in delta over time, for the change in the underlying price. Gamma is positive for both call and put options in this paper.

Theta (θ): Theta measures the impact of change in time expiration. Generally, it is shown in a negative value for both call and put options, indicating the option price decreases each day that is approaching the time of expiry.

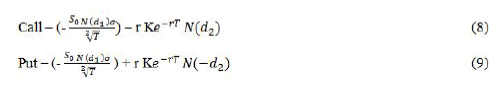
Vega (ν): Measure the impact of change in volatility of the underlying value. Vega is positive for both call and put options in this paper.

Rho (ρ): Measure the impact of change in the interest rate of the underlying value. Generals, call options to have positive Rho value and put options to have negative Rho value (Table 1).

Table 1. Moneyness of options.

Results and Discussion

With relevance to this study, the scholar has calculated the Nifty Call (CE) and Put (PE) options prices and Greeks daily from 1-Nov -2018 to 25-Nov-2018. For analysis purposes, the research scholar has selected Nifty call and put option prices and Greeks on 1- Nov-2018, 09-Nov-2018, 15-Nov-2018, and 29-Nov-2018, the time to expiry or days left is set at 28 days, 20 days, 14 days, and 7 days respectively [27]. The data can be seen in Tables 1-4 for each selected strike price 10900, 11100, 11300, and 10100. Finally, Greeks are computed for each Nifty option poisons and results are discussed below, under each table (Table 2).

Table 2. Nifty CE and PE option price, and Greeks for strike price-10900.

Above Table 2 exhibits the Nifty CE option price, PE option price, and option Greeks for strike price 10900. According to the observations and analysis, on 1-Nov-2018 delta value and option price of a Nifty CE option are higher, 0.73910 and Rs. 353.5 respectively since the Nifty spot price value is higher at 11008.3 when compared to strike price 10900 i.e., the call option contract is ITM (in the money). Later days when the Nifty CE option contract leans toward the expiry date, the delta value decreases to 0.00569 and Nifty call option prices decrease to Rs. 0.4. This is because the Nifty spot value moves down to 10224.75 which leads the contract to OTM (Out of the money) [28]. In the case of Nifty PE option changes in delta and option price values against the same nifty spot value 11008.3 are exactly reversed in nature, i.e., delta value of Nifty PE option and option prices are lower, -0.29059 and Rs. 100.25 respectively because the put option contract is OTM. In the next few days, while Nifty PE option contracts approach the expiry date, the delta value increases to -0.97023, and the put option price increases to Rs. 576.65 as the contract leans towards ITM since the Nifty spot value decreases to 10224.75. The gamma value of both the Nifty CE option and Nifty PE option decreases as the option approaches close to the expiry date 29-Nov-2018 i.e., time left 7 days to expiry. The gamma value is zero for the Nifty CE option which is the OTM option and the Nifty PE option's gamma value is 0.00023 which is the ITM option. Theta value is high for the Nifty CE option on 1-Nov-2018, -5.22075 and this value decreases as the contract approach closer to expiry, and on 22-Nov-2018 value is -1.80049. While analyzing the case of the Nifty PE option theta value is -2.92252 and it increases as the contract approaches expiry on 22-Nov-2018 the value is -7.05144 since implied volatility is more than 54.84%. Rho value for Nifty CE option on 1-Nov-2018 is higher 5.1176 since the contract is ITM and days left to expiration is more i.e., 28 days. In the latter days, the contract tends to OTM, and the days left to expiration are 7 days. Hence Rho value decreases to 0.00149. Rho values for the Nifty PE option on 1-Nov-2018 are -2.16916 and on 22-Nov-2018 are -0.28746 (Table 3).

Table 3. Nifty CE and PE option price, and greeks for strike price-11100.

The above Table 3 shows the analysis for strike price 11100, detailing the Nifty CE option price, PE option price, and option Greeks. According to the above observation and analysis of the Nifty CE option on 1-Nov-2018, the delta value is 0.58375, and the option price is Rs. 212, therefore the contract is ATM (at the money) since the Nifty spot value is 11008.3 almost touching the strike price 11100 [29]. A few more days later, both delta values and option prices get decreased. In 22-Nov-2018 the delta value is 0.00357 and the option price is Rs. 0.25 as the contract becomes OTM towards the expiry date, since the Nifty spot value is 10224.75. The gamma value is more than 0.00093 on 1-Nov-2018 since the contract is ATM which implies that acceleration of change in delta value is more for every point change in the Nifty spot value. A few days later, the contract tends to OTM as it approaches the expiry date of 22-Nov-2018, and therefore gamma value decreases to zero. Thus the option price will not have a significant change in the movement of the Nifty spot value due to high implied volatility i.e., 51.46%. Further, it is observed that Theta and Vega's values are higher on 1-Nov-2018 i.e., -5.11232 and 11.01249 respectively since the contract is ATM. In later days both the values decrease and on 22-Nov-2018 Theta value is -1.48543 and the Vega value is 0.05732 as the contracts tend towards expiry and become OTM. Rho value is higher, i.e., 4.08707 on 1-Nov-2018, because 28 days are left to expiry. As the contract moves to the expiry date of 22-Nov-2018, the Rho value decreases to 0.00097 so it does not affect the option's price [30]. On observing the Nifty PE option on 1-Nov-2018, the contracts are ATM since the Nifty spot value is 11008.3 which are almost equal to the strike price of 11100. Delta value is 0.452527 and has a higher gamma value, i.e., 0.00082. Later days as contracts tend towards expiry and become ITM. Therefore, on 22-Nov-2018 delta value increases and becomes -1 but the gamma value decreases to zero, which indicates that the option price moves up by Rs.1 which proves that for every one point there exists an upward movement in the Nifty spot value. It is also observed that the Nifty PE option price also increases from Rs. 156.2 to Rs. 772.9. On 1-Nov-2018 Theta value is -2.63457 and the Vega value was 11.06321. During the later days observed on 09-Nov-2018 and 15-Nov-2018 steadily the value decreases [31]. But on 29- Nov-2018 Theta value increases to -3.01289 since Vega and implied volatility is zero. It is also observed that higher value Theta does not affect the option price for the Nifty PE option contract is ITM which has more fundamental value and less time value. The analysis also observed that the Rho value is higher at -3.18038 on 1-Nov-2018 and lesser value at -0.30127 on 22-Nov-2018 (Table 4) [32].

Table 4. Nifty CE and PE Option price, and greeks for strike price-11300.

Above Table 4 exhibits the strike price of 11300, along with the Nifty CE option price, PE option price, and option Greeks. The observations and analysis of the Nifty CE option on 1-Nov-2018 in the contract are OTM (On the money) since the Nifty spot value is 11008.3. Consequently have a lesser delta value, 0.38786 and it further decreases to 0.00255 as contracts approach the expiry date on 22-Nov-2018 and become deep OTM since the Nifty spot value moves down to 10224.75. The gamma value is also higher, 0.00097 on 1-Nov-2018, and steadily decreases become zero towards 22- Nov-2018. It is also observed that the Nifty CE option price on 1- Nov-2018 is Rs. 103.9 which decreases to Rs. 0.24 on 22-Nov-2018 as contracts become further deep OTM. Theta and Vega value seem higher on 1-Nov-2018 i.e., -4.2457 and 10.81369 respectively. Further, it is observed that both Theta and Vega value decreases as contracts approach the expiry date of 22-Nov-2018, values are -1.31810 and 0.04252 respectively. Rho value seems higher than 2.73932 on 1-Nov-2018 because 28 days remain to expiry. Rho value seems to decrease to 0.00072 on 22-Nov-2018 as only seven days are left to expire [33]. It is also observed that on 1-Nov-2018 Nifty PE option contract is ITM since the Nifty spot value is 11008.3 reflecting the delta value as 0.59806 and higher gamma value, 0.00089. Movement of contract towards to expiry date proves to become further deep ITM as Nifty spot value increases to 10224.75. Therefore on 22-Nov-2018 value of delta increases to -1, the value of gamma decreases to zero, and obviously, option prices increase from Rs. 241.4 to Rs. 969.9 Rs. It is also observed that on 1-Nov-2018 values of Theta are -1.66531 and Vega is 10.91944. Movement of contract at a later stage, nearing the date of expiry, on 22-Nov-2018 Theta impels a higher value of -3.06767, and Vega decreases to zero due to implied volatility. It is observed that on 1-Nov-2018 Rho value is -4.48764 with 28 days left to expiry, gradually Rho decreased to -0.30677 on 22-Nov-2018 because only seven days were left to expiry (Table 5) [34].

Table 5. Nifty CE and PE Option price, and greeks for strike price-10100.

The above table shows the analysis of Nifty CE option price, PE option price, and option Greeks for strike price 10100. Observations and analysis decipher that on 1-Nov-2018 Nifty CE option contract is deep ITM, proving the Nifty spot value is 11008.3 and the Nifty option price is also higher, Rs. 1068.85. Throughout the life span of the contract, delta value is unconditionally 1 and gamma is zero, as implied volatility Vega is also zero. While the contracts approach the date of expiry, it becomes less ITM i.e., proving that the Nifty spot value travels downwards from 11008.3 to 10224.75, resulting in moving the option price towards descending phase, reaching Rs. 224 on 22-Nov-2018. This behavior is because, though a contract has an absolute delta value of 1 the gamma, Vega and implied volatility is zero which will not reflect many options prices with the movement of the Nifty spot value. It is also observed that the Theta value ranges between -2.72176 to -2.73897 till the expiry of the contract. Rho value is 6.53226 on 1-Nov-2108 in 28 days still pending expiry. On 22-Nov-2018, the Rho value decreased to 0.2738 with only seven days left to expire. Further, it is observed that on 1-Nov-2018 Nifty PE option carries a lesser delta value, -0.04832 as the Nifty spot value is 11008.3 i.e., the contract is deep OTM position. While the contracts approaching the expiry phase, on 22-Nov-2018 delta value went up to -0.07068 as the Nifty spot value falls in descending phase, 10224.75 and the contract becomes lesser OTM. On the 1-Nov-2018 Option, the price was Rs. 14.25 on 10-Nov-2018 its value is Rs. 36.4 due to an increase in Delta value -0.14224 and higher Gamma, 0.00045. Theta value is less on 1-Nov-2018 i.e., -1.30005 compared to the Vega value of 2.8339. In 22-Nov-2018 the Theta value gets increased to -10.43448 due to higher implied volatility of 29.38% and the Vega value falls to 0.72387. On 1-Nov-2018 Rho value is -0.3591 because of the lavish 28 days remaining for expiry, and on 22- Nov-2018 Rho value has decreased to -0.01994 with only seven days left to expiry [35,36].

Conclusion

The research, analysis of five Greeks values–delta, gamma, theta, vega, and rho from above Tables 2 and 5, for strike prices 10900, 11100, 11300, and 10100 respectively; from option Buyer's point of view, it can be summarized that Nifty PE options for strike prices 10900, 11100 and 11300 expired ITM (in the money) on 22-Nov-2018 proving to have a highest upward movement of option prices, Rs. 5765.65, Rs.772.9 and Rs.969.9 respectively making the good sign of profit to the option buyer. While Nifty CE options strike prices 10900, 11100, 11300 expired OTM (on the Money) on 22-Nov-2018 is having a downward movement of option prices, Rs. 0.4, Rs. 0.25 and Rs. 0.24 respectively, creating a loss to the option buyer. In the case of Nifty CE option strike price 10100, initially deep ITM and later expiring to mild, less ITM in 22-Nov-2018, prove to be having a downward movement of the option price, Rs.224 creating relatively a reduced amount of loss to the option buyer. The Nifty PE option strike price 10100 is initially deep OTM and later expiring to the very lees deep OTM having descending movement of the Option price, Rs.4.95 on 22-Nov-2018 making relatively little loss to the option buyer.

The researcher tries to decipher that price of a call option or put option on a non-dividend paying asset is a relative utility of five variables, namely the strike price, expiration time, implied volatility, the spot price of the underlying value, and risk free interest rate. The changes incurred on any one of these variables will certainly affect the option's price. It is relevant to state that each Greek of an option, measures the feeling of an option price relative to changes in the market variables. Consider if the delta value is higher, more probable that an option contract will expire ITM. ATM option will have a delta value of 0.5 and it is subject to rapid change, while the delta value changes slowly for OTM and ITM options. However, if the gamma value is small, changes on delta are slow. It is found that the ATM option has the highest Gamma value when compared to ITM and OTM options. Theta can be defined as the time decaying factor of an option and that helps the trader to classify the right strike price, the right time to trade, and so on. ATM option has a higher theta when compared to ITM and OTM options, while Theta is higher when implied volatility is lower. Black-Scholes Model assumes the volatility constant, but in practical situations, it is dynamic. In general, all option price increases when volatility increases. The effect of volatility is more when surplus time is left for expiry. The research study analyzed that if Vega is positive or negative to an extreme, the option price highly reacts to volatility changes. Let's consider if Vega is close to zero, changes in volatility may have very little impact on the option price. Rho value is larger for the ITM option and decreases as the option leans towards OTM. The value of Rho increases as the time to expiration increases. It is also found that the interest rate will not have much effect on shorter-term option price, but for long-term options like LEAPS, the interest rate will certainly affect the option's price as it will have a greater cost of carry.

Finally, the researcher concludes that the findings have implications for intellectuals who persistently hesitate about the validity of the Black-Scholes model and its assumptions. The study institutes that the option values have inconsequential relevance to the market values. The Greeks are exceptionally useful in helping investors to forecast the pricing efficiency of options in the future since they successfully measure the sensitivity of the option price to market variables. Thus, it helps investors plan an efficient pricing strategy and to identify the best option strikes considering the time to expiry.

Acknowledgment

The authors wish to thank the ICSSR (Indian Council of Social Science Research) for providing the doctoral fellowship. And this may help in effectively writing this research paper.

References

1. Ackert LF and Tian YS. "The Introduction of Toronto Index Participation Units and Arbitrage Opportunities in the Toronto 35 Index Options Markets." J Deriv 5 (1998): 44-53. [Google Scholar]
2. Ackert LF and Tian YS. "Efficiency in Index Options Markets and Trading In Stock Baskets." J Bank Financ 25 (2001): 1607-1634. [Crossref] [Google Scholar]
3. Black F and Scholes M. "The Valuation of Option Contracts and A Test of Market Efficiency." J Finance 27 (1972): 399-418. [Google Scholar]
4. Black F and Scholes M. "The Pricing of Options and Corporate Liabilities." J Political Econ 81 (1973): 637-654. [Google Scholar]
5. Cornell B and French K. "The Pricing of Stock Index Futures." J Futures Mark 3 (1983a): 1-14. [Crossref] [Google Scholar]
6. Canina L and Figlewski S. "The Information Content of Implied Volatility." Rev Financ Stud 6 (1993): 659-681. [Google Scholar]
7. Cavallo L and Mammola P. "Empirical Tests of Efficiency of The Italian Index Options Market." J Empir Finance 7 (2000): 173-193. [Crossref] [Google Scholar]
8. Chesney M, Gibson R and Loubergé H. "Arbitrage Trading and Index Option Trading at SOFFEX: An Empirical Study Using Daily and Intradaily Data." Financ Mar Portf Manag 9 (1995): 35-60. [Google Scholar]
9. Rajanikanth C and Lokanadha Reddy E. "Analysis of Price using Black Scholes and Greek Letters in Derivative European Option Market." Int J Sci Technol Manag 3 (2015): 34-37.
10. Chiras, DP and Manaster S. "The Information Content of Option Prices and A Test of Market Efficiency." J Financ Econ 6 (1978): 213-234. [Crossref][Google Scholar]
11. Cox JC and Ross SA. "The Valuation of Options For Alternative Stochastic Processes." J Financ Econ 3 (1976): 145-166. [Crossref] [Google Scholar]
12. Dumas B, Fleming J and Whaley R. "Implied Volatility Functions: Empirical Tests." J Financ 53 (1998): 2059-2106. [Crossref] [Google Scholar]
13. Evnine J and Rudd A. "Index Options: The Early Evidence." J Financ 40 (1985): 743-756. [Crossref] [Google Scholar]
14. Fontanills GA and Gentile T. "The volatility course." Hoboken, New Jersey, John Whiley and Sons Inc. (2003).
15.  Gemmill GT. "The Forecasting Performance of Stock Options on the London Traded Options Market." J Bus Finance Account 13 (1986): 535-546. [Crossref] [Google Scholar]
16. Kamara A and Miller TW.Jr. "Daily and Intradaily Tests of European put-call parity." J Financ Quant Anal 30 (1995): 519-539. [Crossref] [Google Scholar]
17. Klemkosky RC and Resnick R. "An Ex-ante Analysis of Put-Call Parity." J Financ Econ 8 (1980): 363-378. [Crossref] [Google Scholar]
18. Latane H and Rendleman RJ. "Standard Deviation of Stock Price Ratios Implied by Option Premia." J Financ 31 (1976): 369-382.
19. MacBeth J and Merville L. "An empirical examination of the Black-Scholes call option pricing model." J Financ 34 (1979): 1173-1186. [Crossref] [Google Scholar]
20. Manaster S and Rendleman Jr R. "Option Prices as Predictors of Equilibrium Stock Prices." J Financ 37 (1982): 1043−1057. [Crossref] [Google Scholar]
21. Merton RC. "The Theory of Rational Option pricing." Bell J Econ 4 (1973): 141-183. [Crossref] [Google Scholar]
22. Muthusamy A and Vevek S. "Does B-S-M Model Act as a Canopy to the Investors in Options Market?" Pacific Bus Rev Inte 8 (2015): 91-98. [Google Scholar]
23. Mittnik S and Rieken S. "Put-call Parity and The Informational Efficiency of the German DAX-index Options Market." Int Rev Financ Anal 9 (2000a): 259-279. [Crossref] [Google Scholar]
24. Misra D, Misra SD, Khand V and Nagar G. "Determinants of Violation of Put-call Parity Theorem: A study of NSE Nifty options." Presented at 7^th GCA, New Delhi 15-16, February, 2005. (2005).
25. Nilakantan NS and Shalini Talwar. “Discrete Delta – hedging: Indian Market”. SCMS J Indian Manag 11 (2014): 5-17. [Google Scholar]
26. Nagendran R and Venkateswar S. “Validating Black-Scholes Model in Pricing Indian Stock Call Options”. J Appli Financ Bank 4 (2014): 89-101. [Google Scholar]
27. Saravanan S and Pradeep Kumar G. “Estimation of Stock Option Prices Using Black-Scholes Model”. IJRCMS 2 (2012): 130-136
28. Juneja S. “Understanding the Greeks and their Uses to Measure Risk”. IJRCMS 3 (2013): 2231-5756.
29. Shastri, Kuldeep and Tandon K. "An Empirical Test of Valuation Model for American Options on Futures Contracts." J Financ Quant Anal 10 (1986): 377-392. [Crossref] [Google Scholar]
30. Stoll HR. “The Relationship between Put and Call Option prices.” J Financ 24 (1969): 801-824. [Crossref][Google Scholar]
31. Varma JR. "Mispricing of Volatility in the Indian Index Options Market." IIMA Working Paper, 2002-04-01, (2002). [Google Scholar]
32. Lazibat T and Bakovic T. “Options Hedging As A Mean of Price Risk Elimination”. Ekon Misao Praksa 16 (2007): 63-78. [Google Scholar]
33. Panduranga V. “Relevance of Black-Scholes Option Pricing Model in Indian Derivatives Markets – A Study of Cement Stock Options.” Int J Multidiscip Res Soc Manag Sci 1 (2013): 91-95.
34. Yu, Xisheng and Xiaoke Xie, “On Derivations of Black-Scholes Greek Letters.” Res J Financ account 4 (2013): 80-85. [Google Scholar]
35. Lyuu, Yuh-Dauh and Teng Huei-Wen. “Unbiased and Efficient Greeks of Financial Options.” Finance Stoch 15 (2011): 141-181. [Crossref] [Google Scholar]
36. Yadav, Pradeep K and Pope, Peter F. "Stock Index Futures Arbitrage: International Evidence." J Futures Mark 10 (1990): 573-603. [Crossref] [Google Scholar]