Research Article - (2022) Volume 11, Issue 8
Received: 04-Aug-2022, Manuscript No. JACM-22-73430;
Editor assigned: 06-Aug-2022, Pre QC No. P-73430;
Reviewed: 12-Aug-2022, QC No. Q-73430;
Revised: 18-Aug-2022, Manuscript No. R-73430;
Published:
24-Aug-2022
, DOI: 10.37421/2168-9679.2022.11.486
Citation: Ajileye, Ganiyu and Aminu F.A. “Approximate Solution to First-Order Integro-differential Equations Using Polynomial Collocation Approach.” J Appl Computat Math 11 (2022): 486.
Copyright: © 2022 Ajileye G, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In this study, power series and shifted Chebyshev polynomials are used as basis function for solving first order volterra integro-differential equations using standard collocation method. An assumed approximate solution in terms of the constructed polynomial was substituted into the class of integro-differential equation considered. The resulted equation was collocated at appropriate points within the interval of consideration [0,1] to obtain a system of algebraic linear equations. Solving the system of equations, by inverse multiplication, the unknown coefficients involved in the equations are obtained. The required approximate results are obtained when the values of the constant coefficients are substituted back into the assumed approximate solution. Numerical example are presented to confirm the accuracy and efficiency of the method.
Integro-differential equations • Collocation • Power series polynomial • Shifted chebyshev polynomial
An Integro-differential equation is any type of equation combining an unknown function involving both integral and derivative operators. It is applicable in several fields, such as engineering and science. These equations are either Fredholm, Volterra, or Fredholm-Volterra integro-differential equations. As a result, a numerical method for solving such equations is required. Some numerical approaches in literature for solving integro-differential equations include: Collocation method [1-5], Hybrid linear multistep method [6-8], Differential transform method [9], Perturbed Method [10], Homotopy Perturbation [11], Bernoulli matrix method [12], The Mellin transform approach [13] and Pseudospectral Method [14]. Shahooth et al. presented a numerical method for solving the linear Volterra-Fredholm integro-differential equations of the second kind [15]. This method is called the Bernestein polynomial method. This technique transforms the integro-differential equations into the system of algebraic equations. Some numerical results are presented to illustrate the efficiency and accuracy of this method.
In this work, we consider Volterra Integro-differential equation of the form:
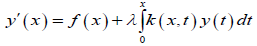
Subject to initial condition;
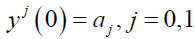
Where yj = djy / dyj y(x) is the unknown function, f(x) is a known function, λ is a known constant and k(x,t) is the integral kernel function.
Basic Definitions
This section defines the basic terms that will be frequently used during the research work.
Definition 1: Standard Collocation Method: This is the method partitioning intervals into different points. For example, let say an interval [a,b], N be the number of collocation points to get the desired collocation points, we use;
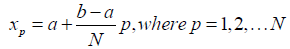
Definition 2: Power Series Polynomial: A power series is basically an
infinite degree polynomial that represents some function. It is generally written
in the form; 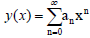 Where an is the coefficient of the polynomials which
are real numbers.
Where an is the coefficient of the polynomials which
are real numbers.
Definition 3: Shifted Chebyshev Polynomials: This is a special type of polynomial generated from Chebyshev polynomial. The shifted Chebyshev has interval [0,1], while Chebyshev has an interval of [-1,1]. The shifted Chebyshev is generated using;
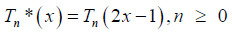
where Tn (x) is the shifted chebyshev term,while Tn (x) is the chebyshev term.
Few terms of the shifted Chebyshev terms are;
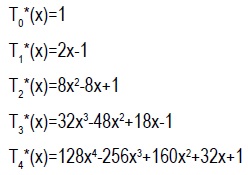
In this section, combination of collocation method and power series approximation is employed for the numerical solution of volterra integrodfferential equations.
Let the solution to (1) and (2) be approximated by (3)
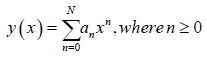
Where an is the real coefficients to be determined, differenting (3) with respect to x, gives
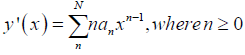
substituting (3) and (4) into (1), gives
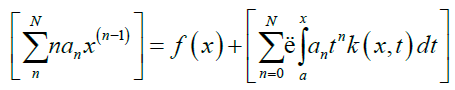
simplifying (5) gives,
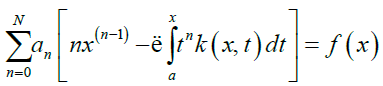
Hence,
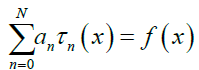
Where
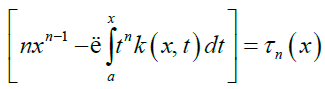
Equation (6) can be written in the form
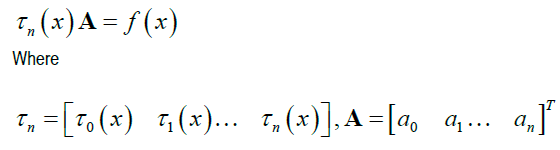
Collocating equation (7) using the standard collocation points
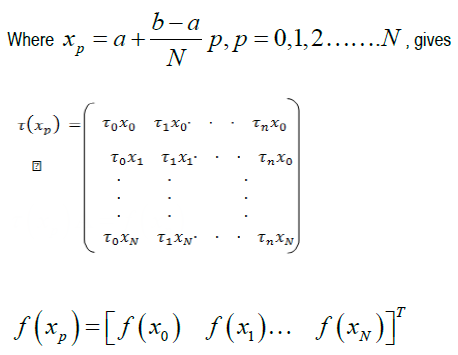
Considering the initial condition,
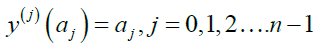
Substituting (3) into (9) we have,
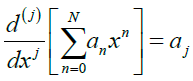
Using equation(10) and equation (8) gives
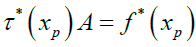
Solving equation (11) using inverse multiplication to get the values of the unknown coefficient an, n=1, 2, …N and substituting the value of the coefficients into the approximate solution gives the numerical results. Repeating the above steps using shifted Chebyshev polynomial as the basis polynomial function, we obtained the approximate solution.
Numerical Examples: In this section, numerical examples with initial conditions are solved to confirm the efficiency and accuracy of the method. Let y_n (x) and y(x) be the approximate and exact solution respectively. Error_N = |y_n (x)-y(x)|.
Example 1: Considering Volterra integro-differential equation
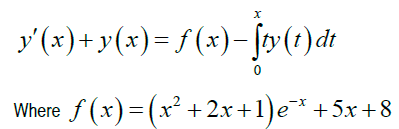
subject to initial condition y(0)=10
Exact solution: y(x)=10-xe-x
Solution 1: Solving at N = 5 using power series polynomial. Substituting approximate solution (3) into example 1 gives
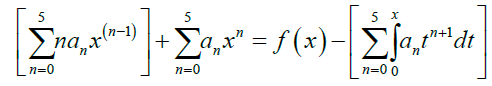
Collecting the like terms gives
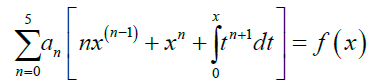
Equation (12) can be written in the form
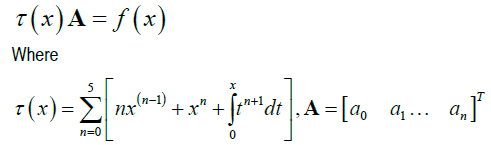
collocating at 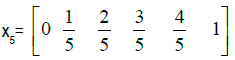 and substituting the initial
conditions gives
and substituting the initial
conditions gives
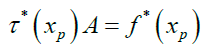
Solving equation (14), we obtained the following approximate solution
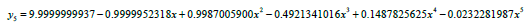
Using the above steps for solving shifted Chebyshev polynomial as the basis polynomial function, we obtained the approximate solution;
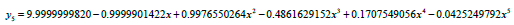
Example 2: Considering Volterra integro-differential equation
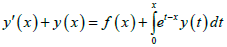
Where f(x)=0
subject to initial condition y(0)=1
Exact solution: y (x) = e−xcosh (x)
Solution 2: Solving at N = 5 using power series polynomial. Substituting approximate solution (3) into example 2 gives
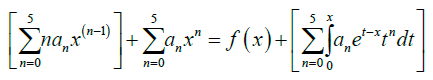
Collecting the like terms gives
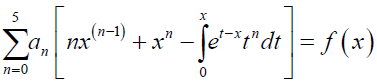
Equation (15) can be written in the form
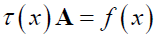
Where
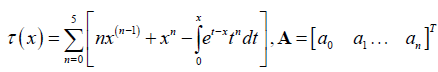
collocating at 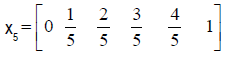 and substituting the initial conditions gives
and substituting the initial conditions gives
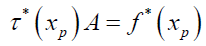
Solving equation (17), we obtained the following approximate solution (Tables 1-4).
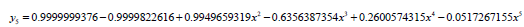
| Xi | Exact Solution | Power Seriesn=5 | Shifted Chebyshevn=5 |
|---|---|---|---|
| 0 | 10 | 9.999999994 | 9.999999982 |
| 0 | 9.909516258 | 9.909509989 | 9.909508005 |
| 0 | 9.836253849 | 9.836242518 | 9.836278452 |
| 0 | 9.777754534 | 9.77774555 | 9.777945271 |
| 0 | 9.731871982 | 9.731868389 | 9.732450172 |
| 1 | 9.69673467 | 9.696733792 | 9.69799158 |
| 1 | 9.670713018 | 9.670710096 | 9.67297361 |
| 1 | 9.652390287 | 9.652383354 | 9.655955045 |
| 1 | 9.640536829 | 9.640529449 | 9.645598296 |
| 1 | 9.634087306 | 9.634086223 | 9.640618379 |
| 1 | 9.632120559 | 9.632125613 | 9.639731878 |
| Xi | Power SeriesN=5 | Shifted Chebyshevn=5 |
|---|---|---|
| 0 | 6.00E-09 | 1.70E-08 |
| 0 | 6.27E-06 | 8.25E-06 |
| 0 | 1.13E-05 | 2.46E-05 |
| 0 | 8.98E-06 | 1.91E-04 |
| 0 | 3.59E-06 | 5.78E-04 |
| 1 | 8.78E-07 | 1.26E-03 |
| 1 | 2.92E-06 | 2.26E-03 |
| 1 | 6.93E-06 | 3.56E-03 |
| 1 | 7.38E-06 | 5.06E-03 |
| 1 | 1.08E-06 | 6.53E-03 |
| 1 | 5.05E-06 | 7.61E-03 |
| Xi | Exact Solution | Power Seriesn=5 | Shifted Chebyshevn=5 |
|---|---|---|---|
| 0 | 1 | 0.999999938 | 0.999999916 |
| 0.1 | 0.909365377 | 0.90934122 | 0.909281555 |
| 0.2 | 0.835160023 | 0.835116552 | 0.834695109 |
| 0.3 | 0.774405818 | 0.774370716 | 0.773063213 |
| 0.4 | 0.724664482 | 0.724648492 | 0.72176967 |
| 0.5 | 0.68393972 | 0.683932578 | 0.678688419 |
| 0.6 | 0.650597106 | 0.650581523 | 0.642112506 |
| 0.7 | 0.623298482 | 0.623267655 | 0.610683052 |
| 0.8 | 0.600948259 | 0.600915006 | 0.583318222 |
| 0.9 | 0.582649444 | 0.582637242 | 0.559142197 |
| 1 | 0.567667642 | 0.567675589 | 0.537414142 |
| Xi | Power SeriesN=5 | Shifted ChebyshevN=5 |
|---|---|---|
| 0 | 6.24E-08 | 8.43E-08 |
| 0.1 | 2.42E-05 | 8.38E-05 |
| 0.2 | 4.35E-05 | 4.65E-04 |
| 0.3 | 3.51E-05 | 1.34E-03 |
| 0.4 | 1.60E-05 | 2.89E-03 |
| 0.5 | 7.14E-06 | 5.25E-03 |
| 0.6 | 1.56E-05 | 8.48E-03 |
| 0.7 | 3.08E-05 | 1.26E-02 |
| 0.8 | 3.33E-05 | 1.76E-02 |
| 0.9 | 1.22E-05 | 2.35E-02 |
| 1 | 7.95E-06 | 3.03E-02 |
The numerical solution of the Volterra integro-differential equation is presented in this study and the results are compared to the exact solution. Power series and shifted Chebyshev polynomials are used as the basis functions.
The numerical results of the examples as shown in tables shows that the results of power series approximation converges to the exact solution than the results of shifted chebyshev approximation. Observation also shows that as the value of x increases i.e. (from 0 to 1), the results of the shifted chebyshev diverges from the exact solutions.
None.
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report