Characterization of Carbon Pellets Prepared from Date Palm Leaves (Phoenix dactylifera L.) by Compression Pressure: X-ray Diffraction Measurements and Applications

Fatima Musbah Abbas^1*, Zehbah Ali Al Ahmad², Rehab Omer Elnour Elgezouly³ and Abubaker Elsheikh Abdelrahman^4
*Correspondence: Fatima Musbah Abbas, King Khalid University, Collage Science and Art, Dhahran Aljanoub, Abha, Saudi Arabia and Biotechnology and Genetic Engineering, National Center Researcher, Khartoum, Sudan, Email:

Keywords

Carbon pellets • Date palm leaves • Compression pressure • Crystallites dimensions • Young’s modulus • Volumetric strain

Introduction

Solid carbon materials have been developed in various physical forms, from reliable products such as powder, granules, and pellets, to increase their industrial applications [1,2]. The shape of the pellet form is particularly useful because it is dense or contains particle sizes closed together in a solid manner. In addition, the shape of pellet form can provide a more fundamental understanding of the physical properties of carbon and the interactions that occur at its surface.

Pure carbon can occur naturally in three allotropic forms: cubic, graphite, and diamond. Graphitic carbon is extremely soft, opaque, and is used as solid lubricant, filler, and electrically conductive. Other part is conventional carbon material such as non-graphite has been used as electrical parts in cars electrodes for fuel cells electrical cables and engineering applications [3]. Recently, carbon material has been used as catalyst supports [4], supercapacitive electrodes [5], electromagnetic wave absorbers and potassium-ion storage mechanism [6,7].

Biomass material widely used to produce carbon material such as Pistachio-nut [8], cellulose fiber [9,10], Lignocellulose [11], olive stones [12], and soybean dregs [6]. Therefore, various attempted methods have been made to improve the solid carbon properties, such as self-adhesive and mechanical properties [13], and thermal properties [14]. Frequently, conversion of the precursor into a fine grain powder by pre-carbonizing at low temperature and grinding of the fine grain powder is very important to improve its self-adhesive properties [13]. This statement comes of predicting the mechanical behavior of the grain particles subjected to different pressure [15,16]. Therefore, the increased compaction pressure reduces the inter-granular distance by reducing the voids, forming a solid bond that can improve the mechanical performance of the solid carbon pellets.

It is well known that X-ray interference intensity offers more or less direct details of the atomic arrangement in crystals structure and detects the crystallite dimensions such as crystallites parameters. An empirical model has been estimated to link a crystallite dimensions and volume fraction with Young’s as a function of annealing temperature by the Emmerich FG, [17] as class of X-ay diffraction application. They consider that the bulk of the carbon matrix was made up of two phase-granular structures (micro-crystallites and cross-links), and at the micro-structural level, the Young’s modulus is controlled by its crystallite parameters.

So far, biomass date palm leaves (Phoenix dactylifera L.) have been used to prepare solid carbon pellets in the present work, as a low cost material, abundant and easily can prepare in a large amount. The objective of this work is to prepare solid carbon pellets from date palm levers and characterize crystallite dimensions, Young’s modulus and volumetric strain experience as a function of compression pressure. Young’s modulus were also estimated by applying a microscopic cross-ling modules [17] by assuming that the changes in Young’s modulus for carbon samples as a function of heat treatment temperature occur similarly as a function of their compression pressure.

Sample Preparation

Materials and methods

The leaves of the date palm (Phoenix dactylifera L.) leaves were collected from date palm trees in rural areas, urban areas, and cities in southern Saudi Arabia. Date palm leaves (DPLs) are cut into small pieces, washed thoroughly with hot distilled water to remove dust and impurities and dried in an oven at 100°C for 1 hour before being pre-carbonized at 280°C in a vacuum chamber for 4 hours, to cause them to shrink and break the palm leaves microstructure and realizing non carbon content [18]. The average weight loss was about 34%, mainly due to the loss of volatile components and tar [19].

Carbonated date palm leaves are pre-made by ball milled for 20 hours to make a fine grain powder that can pass through a 120-micron sieve. The sifted grain powders were stored in clean, self-sealing plastic bags in silica gel until use. Approximately 2 g of grain powder was converted to pellets by applying 5 to 21 metric tons of pressure in a mold of 2.1 cm in diameter and 8.5 cm in length. All grain pellets that exhibited an excellent binding property were measured by bulk density and elastic modulus using ultrasonic techniques, before being carbonized at 1000°C in a nitrogen environment using a multistep heating profile (Vulcan Box Furnace 3-1750). The heating profile schedule was: 1°C/min from room temperature to 375°C keeping for 1 hour before resuming heating at 3°C/min to 800°C and then 5°C/min to 1000°C and finally keeping it for 5 minutes. Then the system was automatically allowed to cool down naturally to room temperature. The obtained carbon pellets were washed thoroughly with distilled water and hot distilled water to remove impurities until a pH concentration of 5, and dried again at 100°C for 2 hours.

The dimensions of the pellet before and after carbonization were measured using a micrometer. The weights of the pellets before and after carbonization were taken using a balance, and their bulk densities were determined from the ratios of their mass to volume. Results are given as the averages of 6 replicates of each sample were analyzed as a function of compression pressure.

X-Ray diffraction (XRD)

The wide angle XRD diffraction scattering intensity data of the solid carbon pellets were obtained using an X-ray diffractometer (Bruker Advanced Solution AXS D8) operated at 40 kV and 30 mA, with Cu Kα- X-ray radiation. The pellets were scanned at 2Ɵ between 1oand 80°, with a step size of 0.04°. The diffraction spectrum was corrected for instrumental line broadening and fitted into a symmetrical Gaussian distribution curve. The crystallite dimension of the solid carbon pellets, such as d002 spacing stack diameter (La) and stack height (Lc) was calculated from the full width at half maximum (FWHM) of the diffraction peaks (002) and (100) using Bragg’s and Deby-Sherrier equations (1) and software trace 1.4 X-ray diffraction program Varian 5 from Diffraction Technology PTG LTD, Australia to evaluate measurement accuracy.

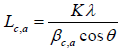(1)

where θ is the scattering angle position, λ is the wavelength of X-ray diffraction, K is a shape factor which is equal to 0.9 for Lc and 1.84 for La, β c, a is the width of a reflection at half-height expressed in radians. For the accuracy measurement the values of d002 and La were fitted to the Takahashi H, et al. [20] expression, demonstrated that a relationship between d002 and Lafor the non-graphitic carbon as a single linear function given as:

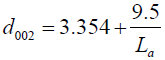(2)

Where 3.354 (Ǻ) is the interlayer spacing of pure graphite.

Lattice constant

The carbon pellets produced are assumed to have a hexagonal structure, and then the lattice constant can be calculated as the following [21].

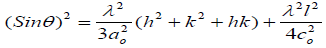(3)

Where (hkl) are Muller indices and co are lattice constants of a graphitic like structure and λ is the X-ray wavelength of 1.54Å.

Ultrasonic measurement

The longitudinal velocity (V) and Young’s Modulus of solid carbon pellets were determined using an Ultrasonic Pulsar-Receiver (Model 500PR) operating at 25 MHZ and equipped with PICO ADC-200 software. The pulsar section produces electrical pulses that are converted into ultrasonic signals using identical transducers. Petroleum jelly (Vaseline) was applied as a coupling medium at the probe sample interface. Reference glassy carbon (Sigradur K) was used to calibrate the ultrasonic signal and measure the samples' longitudinal velocity and Young’s modulus. The glassy carbon scale (Sigradur K) agreed well with the value given by the supplier with an error of < 1%.

The Young’s modulus (E) of the one-dimensional form of the wave equation in a weak attenuation region is given by Deraman M, et al. [13]:

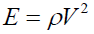(4)

Microscopic cross-linking model

Young’s modulus (E3) of carbon samples as derived by Emmerich FG [17] models is given in Equation (5), considering that the structure of carbon pellets was assumed to be made of granular cubic.

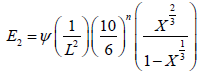(5)

Where, Ψ is a factor that has dimension of force and represents the degree of stiffness of the carbon material, L is the cube root of the mean grain volume and is given as:

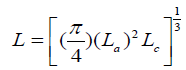(6)

La is the stack diameter and Lc is the stack height of the grain cell and 10/6 is a factor related to strength. n is the order of strength, which is given as:

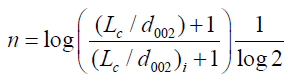(7)

where, i is denoted as structural parameter of the carbon sample taken at initial value (carbon pellet prepared of 5 metric tons considered as initial value, and X is the volume fraction which is given by X=ρ/ρs, where ρ is the density of carbon sample and ρ is the density of a pure graphite [13].

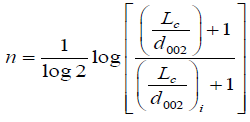(8)

Where i is denoted as a structural parameter of the carbon sample taken at initial value carbon pellet prepared of 5 metric tons of pressure considered as initial value.

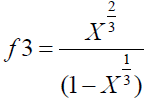(9)

Volumetric strain experience

The change in the volumetric strain (ɛyy) experienced due to change in stress in any direction perpendicular to stress volume is given as:

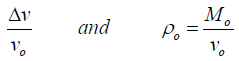(10)

Where v is the volume of the sample after it has decreased by from its initial volume Vo, and Mo is the initial mass of the sample, and its change in the pressure and the original bulk density (ρo) of the sample. The bulk density ρ(ɛ) of the sample as a function of volumetric strain experience is given as:

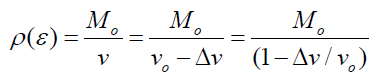(11)

And

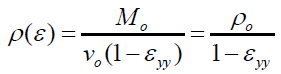(12)

The volumetric strain experienced by the grain pellets from the compression pressure can be considered as ‘corresponding’ to the strain experienced by the SCPs With this ‘corresponding-consideration’, the volumetric strain experience of the SCP was estimated from equation (12).

Results and Discussion

X-ray diffraction (XRD)

Figure 1, represent the X-ray diffraction profile diffraction intensity, initially at (002) and (100) reflection Bragg's peaks, was broad with higher background intensities profiles showing that typical of non-graphitic carbon, indicated that the structure of SCPs is turbostatic [22]. Also, this diffraction profile has been corrected to the background line and fitted to the Gaussian distribution curve, as shown in Figure 1. The Gaussian distribution shows the diffraction profile is broad and overlapped reflection, consist of peaks, i.e., (002), (100), and (004), corresponding to diffraction angles of 25.55°, 45.22° and 54.20° respectively. After correction, the diffraction intensity and Bragg’s peaks were the same as in graphite, and the layer separation was slightly further apart than in graphite as shown in Figure 1.

Crystallite parameters

Table 1, and Figures 2 and 3, shows that the crystallite parameters Lc, and La increased with increasing pressure from 5 to 14 metric tons, and decreasing of the interlayer spacing (d002) with increasing pressure from 5 to 11 metric tons, showing that an improvement in the crystalline dimensions in the Solid carbon pellets, with compression pressure. The increases in Lc and La and parameters in d002 of the CPs indicated that the system behaves more as a graphite-like structure. A similar observation on the carbon based wood (stress breading above 16 metric tons of pressure. 16 metric tons of pressure gave the highest values for Lc, and La, indicating that it is an optimum pressure to prepare grain pellets. Table 1, also show above 11 metric tons of pressure the mean interlayer spacing greatly fluctuated until 16 metric tons and drastically decreased showing that a more crystals has been formed. While decreasing of Lc, and La above 16 metric tons of pressure give use information reduction on the crystals structure. The values of d002, Lc, and La were compared with those of other carbon materials from phenanthrene and polyvinyl chloride (PVC) charred at the same temperature (1000°C) [23]. The d002 and Lc values are close to these values, but Lais less than those of carbon pellets from cotton cellulose Table 1 (Figures 2 and 3).

In addition, the measurement of the d002 and La were found to obey the linear equation of d002 vs. 1/ La where d002, approaches the value for pure graphite structure, where La approaches infinity as shown in Figure 4, and the equation (13) is given as:

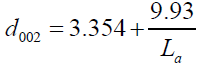(13)

There was good agreement between the constant values of equation, (9.5), for the non-graphitic carbon and that estimated from the fitting data values, (9.93) for Takahashi H, et al. [20]. The values of the d002 explain that the structure of our SCPs sample as (Figure 4) [9].

Lattice constant

The lattice constant values for the hexagonal structure (ao and co) are shown in Table 1, increasing the compressive pressure did not significantly change the lattice constant of the carbon pellets, although there was a decreasing trend, possibly due to a reduction in crystalline structure through the higher amorphous content in the solid carbon pellets or pre-carbonized pellets. We consider that the carbon pellets.

Produced from date palm leaves have similar X-ray diffraction and, therefore, a similar lattice constant. This observation is supported by the results for other indigenous carbon (celluloses). The results also show a significant reduction in the lattice constant compared to pure graphite.

Bulk density

The bulk densities of the pellets were recorded before and after the carbonization process presented in Table 2, and the result of all evaluated solid carbon pellets was low bulk density. The bulk solid density increased but the apparent density decreased slightly after carbonization despite losing considerable weight and significant volume shrinkage. Similar behavior for carbon pellets from oil palm materials [13] cotton cellulose and oil palm stone [7]. On the other hand, the bulk density increased rapidly with increasing compression pressure up to 13 metric tons, indicating that maximum density was achieved. Finally, the density of the solid carbon pellets increased rapidly with compression up to 15 metric tons of pressure and subsequently decreased. It may be due to the dense packing of the material, collapse of the pores and decrease in air gap between the carbon particles as well as improved microstructures, which could be the factors accountable for the increase in mechanical performance (Table 2).

Young’s modulus

Young's modulus of carbonate pellets increased rapidly with compressive stress from 5 to 17 metric tons and decreased to over 17 metric tons, indicating that the increased compaction pressure reduced the inter granular space by reducing voids in the grains (Table 2 and Figure 5). Similar observations also found that Young's modulus of biomass granule carbon from empty palm oil clusters increased linearly with increasing molarity of the acid used to process self-adhesive carbon granules [13] and biomass carbon from heat treatment of bagasse coconut at different temperatures [17].

Increasing compressing pressure from 5 to 17 metric tons returns the carbon pellets with an acceptable Young’s modulus as shown in Table 2 and Figure 5. These results are consistent with the expectation that a precarbonized pellet containing less volatile will develop a better microstructure and stronger inter-particles bonding during carbonization. However, the carbon pellets from PCDPLs are still porous compared to glassy carbon (Sigradur K).

Young’s modulus of pre-carbonized pellets prepared at a pressure of 21 metric tons was the same as that of cotton cellulose. Table 2 also shows that the Young’s modulus of the carbon pellets increased by 1.29 to 1.76 times compared to before carbonization. A similar observation is found in carbon from wood. The Young’s modulus of solid carbon was approximately 1.13 to 1.7 times higher than that of grain pellets (Table 2 and Figure 6).

Microscopic cross-linking model

Estimation of Young’s modulus (3 for the carbon pellets were carried out by fitting the crystallite dimensions and volume fraction to equation 10, by adjusting the value of degree of stiffness (Ψ) until both E2 and E3 were approximately equal as shown in Figure 6 and Table 3. The fit seems to be reasonably good for almost all the data points, except for the data samples prepared at compression pressure below 11 metric tons pressure. It is possibly the crystallite structure is not yet fully developed when the carbon pellet prepared bow 11 metric tons of pressure. The fitted values of x, f1, f2, f3, and E2 are given in Table 3 and Figure 5.

Figure 6 also shows that pressure above 11 metric tons is stable for preparing PCDPL pellets. On the other hand, this increase in Young’s modulus of the carbon pellets can be attributed to the transformation of intermolecular cross-links between chain molecules. The value of degree of stiffness (Ψ) was found to be equal to that given by Emmerich FG [17] for a carbon sample from bagasse coconut, estimated as a function of heat treatment temperature. This result indicates that the degree of stiffness (Ψ) is the same in both carbon samples, even though they were produced from different raw materials and different methods of preparation. The estimate (E3) of the carbon pellets using the microscopic cross-linking model was in good agreement with the experimental data, making it suitable to be used for estimating the Young’s modulus for carbon material. The result also agrees with our assumption that the changes in Young’s modulus for carbon samples as a function of heat treatment temperature occur similarly as a function of their compression pressure (Figure 6).

Volumetric strain experience

The volumetric strain experienced of the SCPs estimated from the equations (5) verses compression pressures are summarized in Table 3 and plotted in Figure 7. Showing that the solid carbon pellets hydrostatic pressure respond to the volumetric strains experience. The apparent volumetric strain experience increased rapidly up to 16 metric tons of pressure as well as showing a fluctuation behavior at large pressure (above 16 metric tons). This fluctuation behavior indicates a stress broadening effects when the grain pellets were subjected to a higher compression pressure. The results also found that 16 metric tons of pressure is the optimum for pelletize the grain powder (Table 3 and Figure 7).

Conclusion

Date palm leaves were found suitable for making carbon pellets without any binding agent, by various compression pressures. The XRD diffraction intensity showed an increasing trend of the crystallite dimensions with the compression pressure. The d002 and Lc values calculated from the broad peak profile were of the value of the same order of magnitude as those obtained for glass-like carbon. The analysis of the d002 and La data was subjected to the linear relation introduced by Takahashi H, et al. [20]. Such compression pressures did not improve the lattice constant of the CPs produced.

The result shows that it is possible to control the bulk density by changing the compression pressure of the PC DPLs powder before carbonization. Increasing pellet pressure was found to be effective in enhancing Young’s modulus. Based on the results, the microscopic cross-linking model can be used to characterize the Young’s modulus of the carbon pellets, where it can identify the origins of microstructure in the carbon sample. It has been shown that it is possible to combine structural properties in a heterogeneous material like carbon to perform such a characterization.

It can be concluded that the crystallite dimensions can play an essential role in the phenomenological description of carbon samples, indicating the applicability of the microscopic cross-linking model. The volumetric strain was increased by increasing the compression pressure up to 13 metric tons, and additional fluctuations because of the stress roasting behaviors at higher compression pressure.

Acknowledgements

The authors extend their appreciation to Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under grant number (GRO/323/43- 1443) and acknowledge to Act Center for the greet support.

Conflict of Interests

None.

References

1. Mareche, J. F., D. Begin, G. Furdin and S. Puricelli, et al. "Monolithic activated carbons from resin impregnated expanded graphite." Carbon 39 (2001): 771-773.

Google Scholar, Crossref

2. Rodriguez-Reinoso, Francisco, M. Molina-Sabio and J. C. Gonzalez. "Preparation of activated carbon-sepiolite pellets." Carbon 39 (2001): 776-779.

Google Scholar, Crossref, Indexed at

3. Lu, Liming, V. Sahajwalla, Chunhua Kong and D. Harris, et al. "Quantitative X-ray diffraction analysis and its application to various coals." Carbon 39 (2001): 1821-1833.

Google Scholar, Crossref, Indexed at

4. Lam, Edmond and John HT Luong. "Carbon materials as catalyst supports and catalysts in the transformation of biomass to fuels and chemicals." ACS Catal 4 (2014): 3393-3410.

Google Scholar, Crossref, Indexed at

5. Rawat, Shivam, Rakesh K. Mishra and Thallada Bhaskar. "Biomass derived functional carbon materials for supercapacitor applications." Chemosphere 286 (2022): 131961.

Google Scholar, Crossref, Indexed at

6. Yue, Jing, Jiaqi Yu, Shaohua Jiang and Yiming Chen, et al. "Biomass carbon materials with porous array structures derived from soybean dregs for effective electromagnetic wave absorption." Diam Relat Mater 126 (2022): 109054.

Google Scholar, Crossref

7. Xu, Jia, Chenyang Fan, Mingyang Ou and Shixiong Sun, et al. "Correlation between potassium-ion storage mechanism and local structural evolution in hard carbon materials." Chem Mater 34 (2022): 4202-4211.

Google Scholar, Crossref, Indexed at

8. Yang, Ting and Aik Chong Lua. "Characteristics of activated carbons prepared from pistachio-nut shells by physical activation." J Colloid Interface Sci 267 (2003): 408-417.

Google Scholar, Crossref, Indexed at

9. Kaburagi, Yutaka, Kohtarou Hosoya, Akira Yoshida and Yoshihiro Hishiyama, et al. "Thin graphite skin on glass-like carbon fiber prepared at high temperature from cellulose fiber." Carbon 43 (2005): 2817-2819.

Google Scholar, Crossref, Indexed at

10. Adinaveen, T., J. Judith Vijaya and L. John Kennedy. "Comparative study of electrical conductivity on activated carbons prepared from various cellulose materials." Arab J Sci Eng 41 (2016): 55-65.

Google Scholar, Crossref, Indexed at

11. Li, Z. Q., C. J. Lu, Z. P. Xia and Y. Zhou, et al. "X-ray diffraction patterns of graphite and turbostratic carbon." Carbon 45 (2007): 1686-1695.

Google Scholar, Crossref, Indexed at

12. Yakout, S. M. and G. Sharaf El-Deen. "Characterization of activated carbon prepared by phosphoric acid activation of olive stones." Arab J Chem 9 (2016): S1155-S1162.

Google Scholar, Crossref, Indexed at

13. Deraman, M., Rahul Omar, Sarani Zakaria and Mardin Talib et al. "Hardness and microstructure of carbon pellets from self‐adhesive pyropolymer prepared from acid and alkaline‐treated oil palm bunch." Adv Polym Technol 23 (2004): 51-58.

Google Scholar, Crossref, Indexed at

14. Şerban, Dan Andrei, Glenn Weber, Liviu Marşavina and Vadim V. Silberschmidt, et al. "Tensile properties of semi-crystalline thermoplastic polymers: Effects of temperature and strain rates." Polym Test 32 (2013): 413-425.

Google Scholar, Crossref, Indexed at

15. Boisot, Guillaume, Lucien Laiarinandrasana, Jacques Besson and C. Fond, et al. "Experimental investigations and modeling of volume change induced by void growth in polyamide 11." Int J Solids Struct 48 (2011): 2642-2654.

Google Scholar, Crossref, Indexed at

16. Delhaye, Virgile, Arild Holm Clausen, F. Moussy and Ramzi Othman, et al. "Influence of stress state and strain rate on the behaviour of a rubber-particle reinforced polypropylene." Int J Impact Eng 38 (2011): 208-218.

Google Scholar, Crossref, Indexed at

17. Emmerich, F. G. "Application of a cross-linking model to the Young's modulus of graphitizable and non-graphitizable carbons." Carbon 33 (1995): 47-50.

Google Scholar, Crossref

18. Radenahmad, Nikdalila, Atia Tasfiah Azad, Muhammad Saghir and Juntakan Taweekun, et al. "A review on biomass derived syngas for SOFC based combined heat and power application." Renew Sustain Energy Rev 119 (2020): 109560.

Google Scholar, Crossref, Indexed at

19. Dhyani, Vaibhav and Thallada Bhaskar. "A comprehensive review on the pyrolysis of lignocellulosic biomass." Renew Energ 129 (2018): 695-716.

Google Scholar, Crossref, Indexed at

20. Takahashi, H., H. Kuroda and H. Akamatu. "Correlation between stacking order and crystallite dimensions in carbons." Carbon 2 (1965): 432-433.

Google Scholar

21. Ungar, Tamas, Jeno Gubicza, Gabor Ribarik and A. Borbely, et al. "Crystallite size distribution and dislocation structure determined by diffraction profile analysis: Principles and practical application to cubic and hexagonal crystals." J Appl Crystallogr 34 (2001): 298-310.

Google Scholar, Crossref, Indexed at

22. Ruland, Wilhelm and Bernd Smarsly. "X-ray scattering of non-graphitic carbon: An improved method of evaluation." J Appl Crystallogr 35 (2002): 624-633.

Google Scholar, Crossref, Indexed at

23. Aso, Hiromi, Koichi Matsuoka, Atul Sharma and Akira Tomita, et al. "Structural analysis of PVC and PFA carbons prepared at 500–1000 C based on elemental composition, XRD, and HRTEM." Carbon 42 (2004): 2963-2973.

Google Scholar, Crossref, Indexed at