Construction of Super NLPDE’s Traveling Waves Solutions of Super KdV Equation with Emphasis to Applications

HI Abdel-Gawad^*
*Correspondence: HI Abdel-Gawad, Department of Mathematics, Faculty of Science, Cairo University, Egypt, Tel: 0020233740201, Email:

Keywords

Super NLPDE’s • Super KdV (kdV6) equation • Traveling waves solutions • Extended unified method

Introduction

Nonlinear partial differential equations NLPDEs occupy a wide area of research in many branches of sciences. They describe complex phenomena in nonlinear systems. Among them, the study of the propagation of waves in optical fiber, electromagnetic waves transmission in communication, and thermopherotic waves in graphene sheets, in electron devices and surface waves in deep water and shallow water waves near shores. Thus, novel dynamic evolution equations are of great interest in nonlinear sciences and in engineering. The present work is of considerable interest in the engineering sciences as well as the mathematical and physical sciences. For example, in chemical industry, the objective is to achieve a great yield of a given product. Which is accomplished by controlling the initial concentration of the reactant. The essence of this work is to inspire the way of controlling the propagation of waves in optical fiber, in fluids, in deep and shallow water

They may reveal new nonlinear phenomena and provide a wide scope of research works. To this issue, different approaches have been developed in the literature, which are the perturbative technique [1-3], the Lax pairs [4,5], the commutator of operators in the symmetries that arise by using the Lie group analysis to nonlinear partial differential equations NLPDE’s, [6,7] and the conservation laws [8-10]. Here, we are interested with the nonlinear Schrodinger NLS and the coupled nonlinear CNLS, Davy- Stewartson DS, The Higgs., and the coupled KdV equations. Applications of NLS are in Bose-Einstein condensation [11,12], fluid dynamics [13-15], plasma physics [16,17], and in optics [18,19]. While the CNLS which in general of the type Gross-Pitaeviskii equation [20-22]. The later has many applications, in optical fiber [23] . the atmospheric gravity waves [24]. Also, it describes condensate dynamics in the limit when the many-body wave function represents the condensate, that is to the low-temperature regime [25]. The DS equation is applicable for water waves theory for internal gravity waves [13] and for ferromagnetism. Also in the study of the envelope gravity solitary waves in Baroclinic atmosphere [15]. In this paper we are concerned with constructing super NLPDEs. In chemical engineering quadratic, cubic, or quartic autocatalytic reactions are described by coupled nonlinear reaction diffusion equations. When analyzing these equations, the initial concentration of a reactant can be be controlled to produce great yield of the required output (product).

Construction of Super PDE’s

Here we consider five cases.

1. The NLS equation which reads

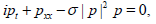(1)

where p is complex function and p=u+iv, thus (1) is rewritten

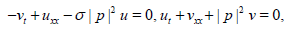(2)

or

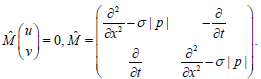(3)

The equation (3) leads to det 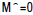, so,we get the operator equation

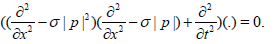(4)

By operating on the functions u₀ and v₀ we have

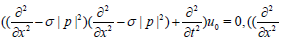
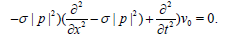(5)

In (5) the functions u0 and v0 are linearly dependents. Thus v₀= A u₀ and we are left with the first equation in (5) which is the super Schrodinger equation.

2. The DS equation in (2+1) dimensions. it reads

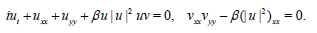(6)

In (6) u=u₁ + iu₂, and it is rewritten

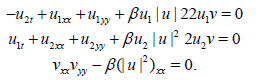(7)

In the operator form equation (7) is

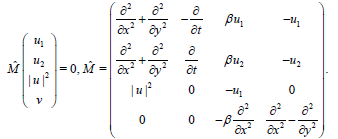(8)

We mention that in (8) the third equation holds identically. Here M̑ is not unique.Thus in this case we can get many super equations. Also, we can have

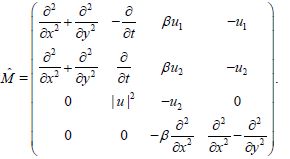(9)

From (8), by setting det M̑=0, we get the first super DS equation,

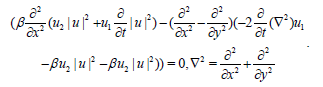(10)

When using (9), we have a second super DS equation, which is

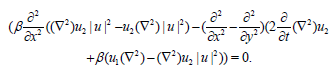(11)

In (10), by replacing (.) by u₁, u₂ and v we have u₂=Au₁, and v=Bu₁ so that (10) reduces to

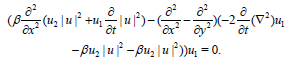
By the same way we get the second super DS equation.

3. The Higg’s equation

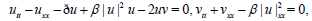(12)

where u is complex function, u=u₁+iu₂, v is real, and (13) is

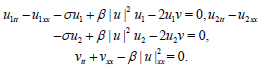(13)

From the equations for u₁ and u₂, we find that they are linearly dependent, that is In the operator form (14) is

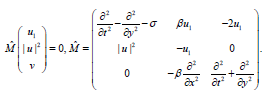(14)

Finally the super Higg’s equation is

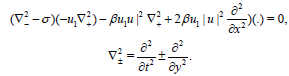(16)

In (16) we replace (.) by u₁ and v, and also we have v= Bu₁, so , we have (16) is

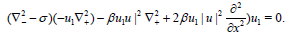(16)

4. The CNLS equation. It reads

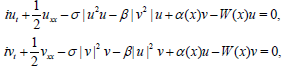(17)

Where u and v are complex functions, u= u₁ + iu₂, v= v₁+iv₂ and (18) becomes

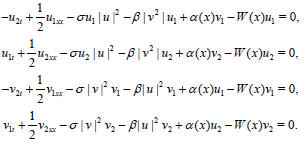(18)

In the operator form of (19) is

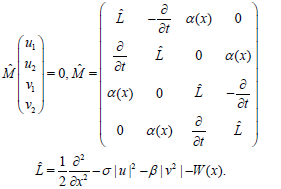(19)

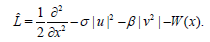
By the same way as in the super NLS equation, here the super equation is

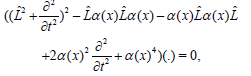(20)

And L̑ is defined in (20). By replacing (.) by u_i,v_ii = 1,2, we get four equation with the same operator. So, each pair is linearly dependent and we have u₂= Au₁, v₁=Bu₁ and v₂ = Cu₁. Finally (20) is rewritten

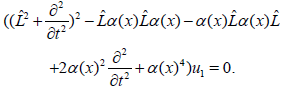(21)

5. The coupled KdV equation which t reads

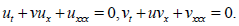(22)

In the operator form, (23) is written

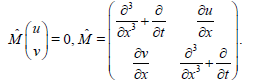(23)

By the same way and by bearing in mind that v= Au, we get

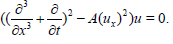(24)

It worthy to notice that (25) is an another version to the KdV6 which was obtained and studied in [26-29].

Traveling wave solutions of the super KdV equation

Here the equation (25) is considered.The traveling wave solutions TWS of (25) are found by using the unified methods [26-31].To this end we use the transformations u (x,t) = v(z) and z= βx+ γt.

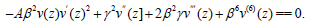(25)

By the methods in some studies [30,31], solutions are expressed for, by the form of polynomial, or rational, function, in an auxiliary function that satisfies an auxiliary equation. In the case of so solution which is a polynomial function, we write

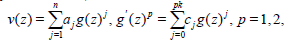(26)

Where p=1 or p=2 The solution of auxiliary equation is elementary or periodic (or elliptic) solutions respectively. In (28) the values of n and k are determined from the balance and consistency conditions. When p=1, we have n=2 (k-1) and 1≤k≤ 13/5.. For details see [30].

In the case of single wave rational function solution, we have

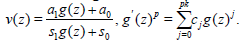(27)

Theorem 1: A necessary condition that a NLPDE has a periodic (or elliptic) solution is that all terms are of even or odd derivatives with p=2 and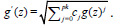

Proof: In the case of even order derivatives, then after calculation each term is free from the square root, so that the equations result are also free. In the case of odd order derivatives all terms factored by the square root and also the equations result are, thus, free.

Theorem 2: A sufficient condition for the existence of periodic (elliptic) solutions is that the solutions of the equation obtained are consistent. By theorem1, (26) has no periodic (elliptic) solutions so we are concerned with the case p=1.

Now we find the TWS by using (27) and distinguish the following cases:

(i)-Case of quadratic auxiliary equation when k=2 in (27),

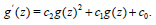(28)

By substituting from (29) into the first equation in (27), calculations give rise to

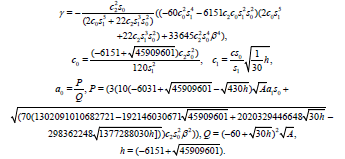(29)

The solution of the auxiliary equation is

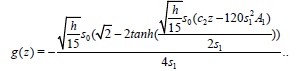(30)

Finally the solution of (26) is

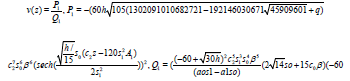(31)

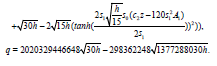
The results in (32) are displayed in Figure 1a against x and t.

Figure 1a The results in (32) are displayed against x and t when

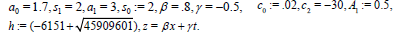
Figure 1b. The results in (37) are displayed against x and t

Figure 1a shows lump soliton wave with periodic wave background, while Figure 1b shows soliton wave with double kinks.

(ii)-Multi linear auxiliary equations which are taken,

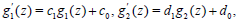(32)

and the solution is

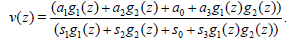(33)

By using v(z) = w (z) inserting (33) and (34) into (26) calculations give

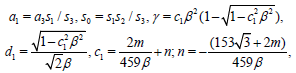(34)

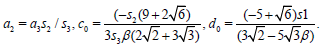
We have

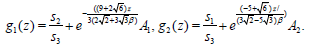(35)

By inserting (35) and (36) into (34),we get

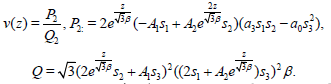(36)

The results in (37) are displayed against x and are shown in Figure 1b.

(iii)-Coupled auxiliary equations

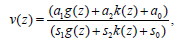(37)

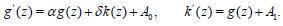
By the same way we have

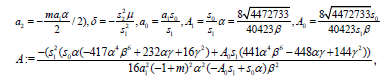
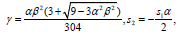(38) and

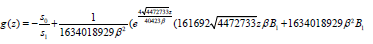(39)

and

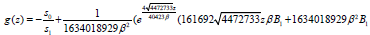(40)

By inserting (39) and (40) into into the second equation in (38) The results are too lengthy to be produced here. The solution obtained is displayed against x and t in Figure 2.

The results for the solution are displayed against x and t.

When,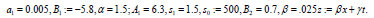

This figure exihibts solitary wave.

(iv)-Coupled auxiliary equations. When

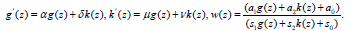(40)

By the same way we have

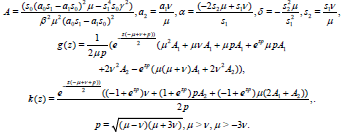(41)

When μ < v, μ>-3v, we have

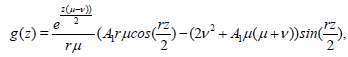
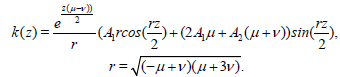(42)

Thus we have two solutions that correspond to the auxiliary functions in (42) and (43) and they are respectively

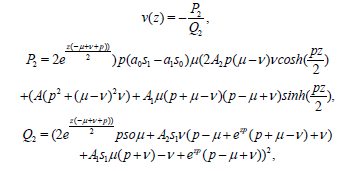(43)

and

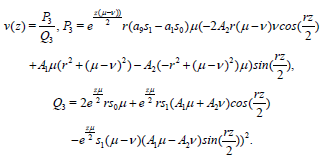(44)

The solutions (44) and (45) are displayed against x and t in Figures 3a and 3b respectively

Figure 3a when,

Figure 3b when,

Figure 3a shows soliton wave with double kinks, while Figure 3b shows lump solitary wave.

The comparison between the method used here and the known methods is done in the following:

1. In This paper the unified method, presented by the author, was used. After this nomenclature , this method unifies all known methods such as, the tanh , modified , and extended versions, the F-expansion, the exponential, the G’/G expansion method, The Kerdyashov methods [30].

2. On the other hand the extended unified method proposed, also by the author may be sufficient to replace the analysis of using the symmetries by inspecting the symmetries that arises by using Lie group [31].

3. Using the generalized unified method, presented by the author, is more powerful tool than using the Hirota method [31].

Conclusions

We have constructed Some super (novel) NLPDE’s equations which describe highly disperive waves in nonlinear systems in optical fiber, Bose Einstein condensate, in ferromagnitism and in deep and shallow water.. Among these equations the super KdV which is known in the literature by the KdV6. This last equation is studied and a class of traveling waves solutions are obtained. These solutions exhibit solitary, soliton with double kinks waves and lumps. We think that this work will lead to a new trend of research when treating the novel NLPDEs found in this work. That may lead to reveal many comlex phenomes in nonlinear optics, fulid and nonlinear waves in shallow water.

References

1. Biswas, Anjan, and Saima Arshed. "Optical solitons in presence of higher order dispersions and absence of self-phase modulation." Optik 174, (2018): 452-459.
2. Xue, Chen, Ean Pan, and Shang Zhang. "Solitary waves in a magneto-electro-elastic circular rod." Smart materials and structures 20, (2011): 105010.
3. Arshed, Saima. "Two reliable techniques for the soliton solutions of perturbed Gerdjikov–Ivanov equation." Optik 164 (2018): 93-99.
4. Habibullin, Itagam, and Arunacalm Khakimova. "On a method for constructing the Lax pairs for integrable models via a quadratic ansatz." Journal of Physics A: Mathematical and Theoretical 50, (2017): 305206.
5. Vasilyev, Madafra, and Akinen Zotov. "On factorized Lax pairs for classical many-body integrable systems." Reviews in Mathematical Physics 31, (2019): 1930002.
6. Toppan, Francesco. "Symmetries of the Schrödinger equation and algebra/superalgebra duality." In Journal of Physics: Conference Series 597, (2015): 012071.
7. Khalique, Chaudry Masood, and Isaiah Elvis Mhlanga. "Travelling waves and conservation laws of a (2+ 1)-dimensional coupling system with Korteweg-de Vries equation." Applied Mathematics and Nonlinear Sciences 3, (2018): 241-254.
8. Maddocks, John, and Donald J Dichmann. "Conservation laws in the dynamics of rods." Journal of elasticity 34, (1994): 83-96.
9. Adhikari, Sadhan K. "Bright solitons in coupled defocusing NLS equation supported by coupling: Application to Bose–Einstein condensation." Physics Letters A 346, (2005): 179-185.
10. He, Janfgral, Charalampidis Eanfr, Kevrekidis Padnee, and Frantzeskakis Duvade. "Rogue waves in nonlinear Schrödinger models with variable coefficients: application to Bose–Einstein condensates." Physics Letters A 378, (2014): 577-583.
11. Meng, Qing, Bin He, and Wei Liu. "Exact similarity and traveling wave solutions to an integrable evolution equation for surface waves in deep water." Nonlinear Dynamics 92, (2018): 827-842.
12. Abdel-Gawad, HI "Waves in deep water based on the nonlinear Schrödinger equation with variable coefficients." Canadian Journal of Physics 92, (2014): 1158-1165.
13. Zhao, Baojun, Ruyun Wang, and Hongwei Yang. "Three-Dimensional Coupled NLS Equations for Envelope Gravity Solitary Waves in Baroclinic Atmosphere and Modulational Instability." Mathematical Problems in Engineering 2018 (2018).
14. Xu, Tao, Chun-Yi Zhang, Guang-Mei Wei, Juan Li, Xiang-Hua Meng, and Bo Tian. "Symbolic-computation construction of transformations for a more generalized nonlinear Schrödinger equation with applications in inhomogeneous plasmas, optical fibers, viscous fluids and Bose-Einstein condensates." The European Physical Journal B 55, (2007): 323-332.
15. Lee, J-H., Oktay K PASHAEV, Colin Rogers, and WK Schief. "The resonant nonlinear Schrödinger equation in cold plasma physics. Application of Bäcklund–Darboux transformations and superposition principles." Journal of plasma physics 73, (2007): 257-272.
16. Arshad, Muhammad, Aly R Seadawy, and Dianchen Lu. "Bright-dark solitary wave solutions of generalized higher-order nonlinear Schrödinger equation and its applications in optics." Journal of Electromagnetic Waves and Applications 31, (2017): 1711-1721.
17. Wazwaz, Abdul-Majid. "Bright and dark optical solitons for (2+ 1)-dimensional Schrödinger (NLS) equations in the anomalous dispersion regimes and the normal dispersive regimes." Optik 192 (2019): 162948.
18. Yu, Fajun. "Localized analytical solutions and numerically stabilities of generalized Gross-Pitaevskii (GP (p, q)) equation with specific external potentials." Applied Mathematics Letters 85 (2018): 1-7.
19. Yu, Fajun, and Li Li. "Inverse scattering transformation and soliton stability for a nonlinear Gross-Pitaevskii equation with external potentials." Applied Mathematics Letters 91 (2019): 41-47.
20. Chen, Junchao, and Biao Li. "Three-Dimensional Bright–Dark Soliton, Bright Soliton Pairs, and Rogue Wave of Coupled Nonlinear Schr¨ odinger Equation with Time-Space Modulation." Zeitschrift für Naturforschung A 67, (2012): 483-490.
21. Liu, Ping, Zi-liang Li, and Sen-yue Lou. "A class of coupled nonlinear Schrödinger equations: Painlevé property, exact solutions, and application to atmospheric gravity waves." Applied Mathematics and Mechanics 31, (2010): 1383-1404.
22. Bodenschatz, Eberhard, Werner Pesch, and Guenter Ahlers. "Recent developments in Rayleigh-Bénard convection." Annual review of fluid mechanics 32, (2000): 709-778.
23. Yu, Fajun. "Inverse scattering solutions and dynamics for a nonlocal nonlinear Gross–Pitaevskii equation with PT-symmetric external potentials." Applied Mathematics Letters 92, (2019): 108-114.
24. Kupershmidt, Boris A. "KdV6: an integrable system." Physics Letters A 372, (2008): 2634-2639.
25. Mirzazadeh, Mohammad, Mostafa Eslami, and Anjan Biswas. "1-Soliton solution of KdV6 equation." Nonlinear Dynamics 80, (2015): 387-396.
26. Abdel-Gawad, HI. "On the “$${\hat {\varvec {kp}}} $$-operator”, new extension of the KdV6 to (m+ 1)-di mensional equation and traveling waves solutions." Nonlinear Dynamics 85, (2016): 1509-1515.
27. Wazwaz, Abdul-Majid. "The integrable KdV6 equations: multiple soliton solutions and multiple singular soliton solutions." Applied Mathematics and Computation 204, (2008): 963-972.
28. Abdel-Gawad, HI. "Towards a unified method for exact solutions of evolution equations. An application to reaction diffusion equations with finite memory transport." Journal of Statistical Physics 147, (2012): 506-518.
29. -Gawad, HI, Hamdy, Nasser S. Elazab, and Mohamed Osman. "Exact solutions of space dependent Korteweg–de Vries equation by the extended unified method." Journal of the Physical Society of Japan 82, (2013): 044004.
30. Abdel-Gawad, HI, and Anjan Biswas. "MULTI-SOLITON SOLUTIONS BASED ON INTERACTIONS OF BASIC TRAVELING WAVES WITH AN APPLICATION TO THE NONLOCAL BOUSSINESQ EQUATION." Acta Physica Polonica B 47, (2016).
31. Srivastava, Hamarad, HI Abdel-Gawad, and Khaled M Saad. "Stability of Traveling Waves Based upon the Evans Function and Legendre Polynomials." Applied Sciences 10, (2020): 846.