Deduction of the Time Fractional Thermal Diffusion Equation from the Classical Thermal Diffusion Equation

Rasolomampiandry G^1*, Rakotoson R² and Randimbindrainibe F^3
*Correspondence: Rasolomampiandry G, Cognitive Sciences and Applications Research Laboratory, BP 1500, Ankatso - Antananarivo 101, Madagascar, Email:

Keywords

Fractional calculus • Dimension-Diffusion

Introduction

Fractional calculus (FC), involving derivatives and integrals of non-integer order, is the natural generalization of classical calculus, which in recent years has become a powerful and widely used tool for better modeling and control of processes in many fields of science and engineering [1-5]. Many physical phenomena have an “intrinsic” fractional order description and therefore FC is needed to explain them [2]. In many applications, the FC provides more accurate models of physics than ordinary calculus. Since its success in describing anomalous scattering [11-17], non-integer order calculus in both one-dimensional and multidimensional space, it has become an important tool in many fields of physics, mechanics, chemistry, engineering, finance and bioengineering [7-10]. Fundamental physics considerations in favor of using models based on non-integer-order derivatives are given in [6-14]. Additionally, fractional derivatives provide an excellent tool for the description of memory and the hereditary properties of various materials and processes [13]. These are advantages of FC compared to classical integer order models, in which such effects are indeed neglected.

In this article, we will consider the general form of the thermal diffusion equation, we will transform it into a time fractional thermal diffusion equation, taking into account the dimensionality of time.

To do this, in section 2, we will make the choice of the fractional derivative used and what it is necessary to respect to change the ordinary derivative of time into a fractional derivative. And the use of the results thus obtained to have the primary objective. Before the conclusion, we will focus on a discretization and a numerical simulation of the equation obtained.

Time Fractional derivatives and dimensionality

Fractional derivatives

To analyze the dynamic behavior of a fractional system, it is necessary to use an appropriate definition of fractional derivative. Indeed, the definition of the fraction and the derivative of order is not unique and there are several definitions, including: Grunwald-Letnikov, Riemann-Liouville, Reisz and the representation of Caputo, and so on. In the case of Caputo, the derivative of a constant is zero and we can define, correctly, the initial conditions for fractional differential equations which can be treated using an analogy with the classical case (ordinary derivative). The Caputo derivative also involves a memory effect by means of a convolution between the derivatives of integer order and a power of time. For this reason, in this article we prefer to use the fractional derivative of Caputo.

The fractional derivative of Caputo for a function of time f (t) is defined as follows [13], when the order of the derivative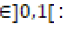

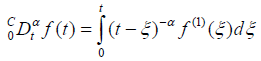           (1)

Sizing of the variable ‘t’

For a thermal diffusion equation, the variable‘t‘represents the time in seconds. We will propose a simple procedure to construct the time fractional thermal diffusion equation. To do this, we replace the time ordinary derivative operator with the fractional as follows:

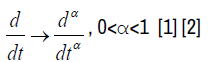        (2)

We can see that (2) is not quite exact, from a physical point of view, because the derivative operator of time 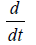has for dimension the inverse of the second s⁻¹ and that of the operator of the fractional derivative of time is 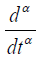. In order to be consistent with the dimensionality of time we introduce the new parameter σ with the following way:

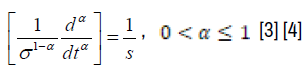        (3)

where α is an arbitrary parameter which represents the order of the derivative. In the case where α = 1, expression (3) becomes an ordinary derived operator. In this way (3) is dimensionally consistent if and only if the new parameter has the dimension of time [σ] = s. Hence we have a simple procedure to construct fractional differential equations. It consists to replace in the following, the ordinary derivative in the ordinary differential equation by the fractional derivative operator:

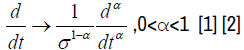         (4)    

Expression (4) is a time derivative in the usual sense, because its dimension is s⁻¹ . The parameter σ (auxiliary parameter) represents the fractional time components in the system [3,4].

Expression of the fractional thermal diffusion equation

If t is the temporal variable and x the spatial variable, the classical thermal diffusion equation is written:

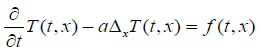           (5)

• ‘a’ is the diffusivity coefficient

• T(t, x) is the temperature corresponding to the variables t and x

• f (t, x) is the second member of equation (1) for the variables t and x

• t> 0 and x belongs to a certain domain of space

From the previous paragraph the fractional thermal diffusion equation with respect to time is written

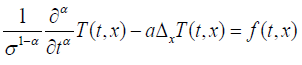
In our case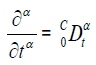

Finally, the fractional thermal diffusion equation with respect to time is written:

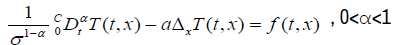            (6)

Note:

The parameter α , which represents the order of the fractional derivative, can be related to the parameter σ, which characterizes the presence of fractional structures in the system. For the present case, referring to the principle taken in [3] and [4], (6) is written:

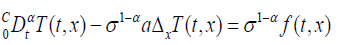
And we take α =σ a ,(6) is written:

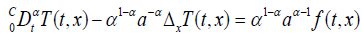         (7)

Discretization and simulation

Discretization

For our discretization, it suffices to consider the variable x only on the real line because σ has no impact on the spatial variable:

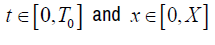
On the segment [ 0,T₀ ], we build a finite sequence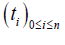 such that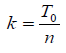

and t_i = ik - Similarly, on the segment [0, X ] , a finite sequence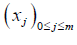

such that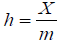 and x_j = jh

According to [5]

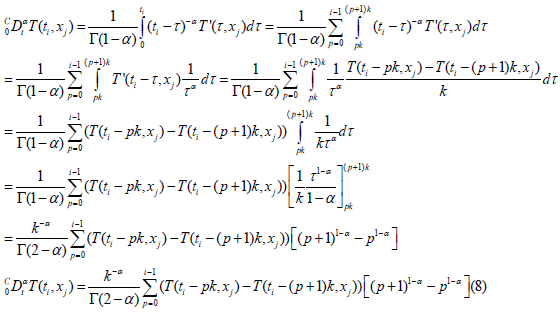
This relation is valid for i ≠ 0

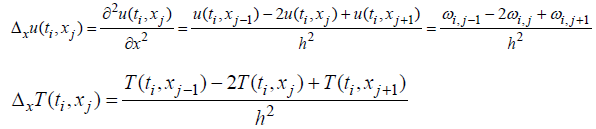
(7) Is written :

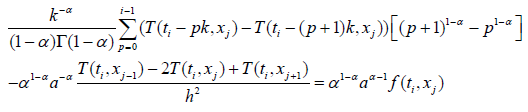
More precisely

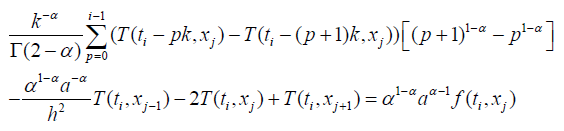
Simulation

Make T₀ =1; X₀ = 2 , 0 <α <1 and we take as an initial condition T(0, x) = 0

for all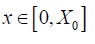

The boundary condition is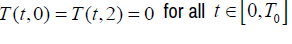

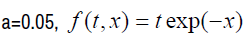
(9) can still be written:

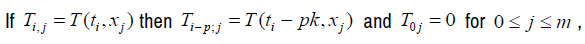
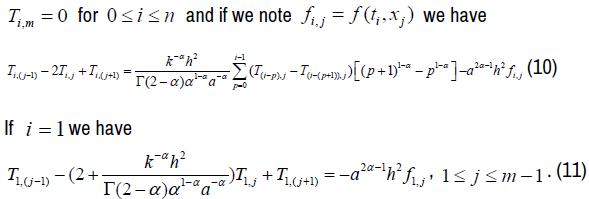
If we vary j, we have m equations:

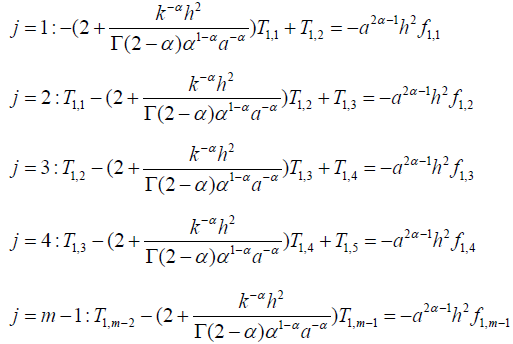
We have the following matrix representation:

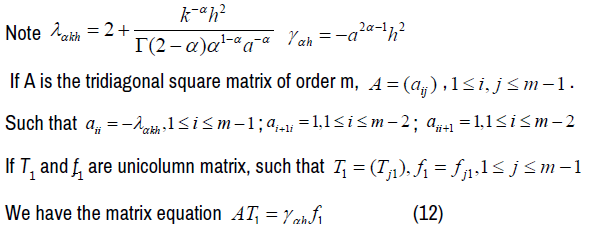
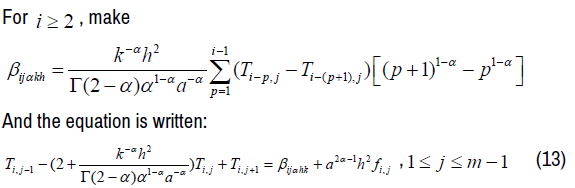
And we have a matrix equation similar to the case i = 1. Thus, we have n matrix equations:

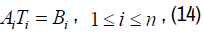
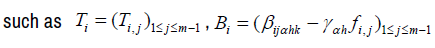
Solving these equations, gives us the values of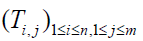

From the above mentioned data, from MATLAB software, we get the following graphical representation:

Conclusion

The important point for this article is the introduction of the parameter ‘σ ‘ in the case of the fractional thermal diffusion equation with respect to time. But the problem that still arises is the identification of the expression of ‘σ’ in the general case, i.e: Is it possible to give a method to search ‘σ’ for all cases.

References

1. Baleanu D, Diethelm K, Scalas E, and Trujillo Juan J. “Fractional Calculus Models and Numerical Methods.’’ Series on Complexity, Nonlinearity and Chaos (2012) :428.
2. Baleanu Dumitru, Golmankhaneh A K, Ali Golmankhaneh K and Nigmatullin R. R.“ Newtonian law with memory.’’ Nonlinear Dynamics.60 (2010):81-86.
3. Gomez-Aguilar JF, Razo-Hernández R and Granados-Liebermanb D . “A physical interpretation of fractional calculus in observables terms: analysis of the fractional time constant and the transitory response.’’ Rev. mex. Fis 60 2014
4. Gomez-Aguilara J.F. Razo-Hernández R, Granados-Lieberman D. “Fractional mechanical oscillators’’Rev. mex. fis 58(2012):348-352
5. Keith Oldham and Spanier J. “The Fractional Calculus Theory and Applications of Differentiation and Intégration to Arbitrary Order.’’Elsevier 1974.
6. Agrawal OP, Tenreiro-Machado J.A and Sabatier I. “ Application of Fractional Derivatives in Thermal Analysis of Disk Brakes’’. Nonlinear Dynamics38(2004): 191–206
7. Yang Q, Liu F and Turner I. “Numerical methods for fractional partial differential equations with Riesz space fractional derivatives.” j.apm .34(2010): 200-218
8.  Robert Janin . “Dérivées et intégrales non entières’’
9. Robert Janin . “Dérivées et intégrales non entières’’
10. Magin L Richard. “Fractional Calculus in Bioengineering”. Crit Rev Biomed Eng. 32 (2004):1-104
11. Shantanu Das. “Functional Fractional Calculus for System Identification and Controls Functional Fractional Calculus’’ Springer 2008 .
12. Samko  Stefan ,  Kilbas A.A and Marichev O I. “Fractional Integrals and Derivatives, Theory and Applications.’’ Gordon and Breach Science 1993.
13. UchaikinVladimir V. “Fractional Derivatives for Physicists and Engineers.’’2008.