Evaluated 149,152,155 &161Tb Production Cross-Sections Using Gd(p, xn)Tb Reactions Near and Above Thershold

Kailash Pandey^* and D P SIngh
^*Correspondence: Kailash Pandey, Department of Physics, University of Petroleum and Energy Studies, India, Email:

Keywords

Tracer radio-isotope • Statistical model • Radio-pharmaceutical

Introduction

Our knowledge of nuclear properties initially restricted to the basic physics, has now spawned many applications in other areas of science and beyond as in forensic science, materials science, biology and last but not least in nuclear medicine. Various radio-isotopes are now frequently used for the diagnostics and therapy of certain diseases in nuclear medicine [1-4]. The very first reported use of radio-isotopes in nuclear medicine was in 1946, when 131I was used successfully for the treatment of thyroid cancer [5]. Since then, various isotopes have been produced through different nuclear reactions and applied not only for the treatment of several diseases, but also as diagnostic and therapeutic tools [6,7]. To an estimate about 140 radio-isotopes among 3000 are used worldwide for medical purposes [8]. Additionally, the medically related radionuclides are commonly used for diagnosis, treatment and research [9,10]. The production of radio-nuclides is on a high rise in recent years because of wider application in advanced technological tools used in nuclear medicine. A reliable path way for the production of these radio-nuclides is thus, required for meeting the high demand of these isotopes. Impurity issues always occur, in general, with the production of these radio-isotopes. Indeed, the accurate nuclear data are required for a hard control of radio-nucleidic purity [11]. In this context, nuclear model calculations can rapidly help to predict unknown nuclear data and thus improved model calculations are of considerable significance [12-16]. The different calculation codes are available and these codes could be used to obtain accurate data for medical radioisotope production [17-20].

In the context of nuclear medicine, Tb is a very special element because it has four different isotopes (out of 13) i.e., 149Tb, 152Tb, 155Tb and 161Tb applicable for therapeutic and/or diagnostic purposes [21]. Due to their chemical similarity, radio-pharmaceuticals for therapy and diagnostics can be made with exactly the same pharmacological properties (e.g. uptake, targeting, bio-distribution). Therefore, the Tb isotopes are very useful for theranostics, where therapy and diagnostics are combined to improve the effects of the treatment [21]. The importance and use of various radio-sisotopes for diagnostic and therapeutic purposes is increasing with the advent of improved technologies in medical industry. The non-destructive nature of these radioisotopes makes them suitable for diagnostic purposes [22]. Technologies such as Positron Emission Tomography (PET), Single Photon Emission Computed Tomography (SPECT) and the radionuclide therapy are the three modalities in nuclear medicine [23,24]. An important aspect while choosing radio-isotope for diagnostic and therapeutic purposes, is the lifetime of the isotope, which governs its use in medicine. The significance of Tb lies in the fact that it offers a number of clinically interesting radio-isotopes, which are together termed as quadruplet of Tb radionuclide having complementary physical decay characteristics [25-27]. There are large no of isotopes of Tb having alpha, beta and EC as the decay modes, thus depending on the use, the desired isotopes may beselected.

¹⁴⁹Tb emits short range α-particles (17%) of 3.967 MeV with a half-life of 4.16 hours and extensively used for radionuclide α-therapy. Moreover, it also emits EC/β+ (83%) of 0.73 MeV and may be used for PET [21]. ¹⁵²Tb is a positron emitter that emits positrons (100%) of an average energy of 1.080 MeV having half-life of 17.5 hours, therefore, it is suitable for imaging using PET [21]. ¹⁵⁵Tb decays by EC (100%) of half-life 5.32 days and can be applied for SPECT [21]. Another terbium isotope of interest is ¹⁶¹Tb that emits low energy electrons with an average energy of 0.154 keV (100%). Additionally, it emits Auger electrons [22] and γ-rays with an energy of 48.92 keV (17%), 57.19 keV (1.8%) and 74.57 keV (10%), therefore, can be used for Auger therapy and for SPECT as well [21]. In the present work, theoretical calculations have been done for the production cross-section of ¹⁴⁹Tb, ¹⁵²Tb, ¹⁵⁵Tb & ¹⁶¹Tb, using nuclear model codes EMPIRE 3.2 [18] & PACE4 [19] based on Hausher Feshback approach and compared with TENDL-2019 library (calculated by TALYS code) [20]. The significance of the present work lies in the fact that, despite having a high potential of these radioisotope for therapeutic and diagnostic purposes owing to their characteristics, very little experimental data is available in literature (Table 1).

Theoretical calculations

The nuclear reaction codes are instrumental for predicting the crosssections and spectra which have not been measured or need to be interpolated/ extrapolated in certain energy regime. Thus the theory based modelling is a viable way to generate complete and consistent nuclear data files. There are several model codes for evaluating nuclear cross-sections such as TALYS [20], EMPIRE [18], PACE4 [19] and GNASH [28]. In the present work, we EMPIRE, PACE and TALYS codes have been used for calculations.

Empire is a statistical modular code using advanced implementation of the Hausher Feshbach Theory [29]. For the present calculations, we have used this code for theoretical investigation of the unclear reaction leading to the production of the radionuclides ^{149, 152, 155 & 161}Tb. The production cross-section of the radio-isotope depends largely on the parameters such as the transmission coefficients, level densities and projectile energy, etc. In the present work the cross-sections are calculated using the formula;

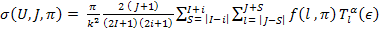(i)

Where, k is the wave number of relative motion & i, I, J and S indicate projectile, target, compound nucleus and channel spin respectively and l is the orbital angular momentum of the projectile a. The function f(l, π) ensures parity conservation. It is unity, if p*P*(−1)^l = π and zero otherwise. Here p, P and π are projectile, target and compound nucleus parities while ε and U stand for the projectile and compound nucleus energy.

In the present case, the projectile is proton (A ≤ 4), the transmission coefficient entering the above equation are calculated using sub routine code Sequential Iteration method for Coupled Equations ECIS [30]. This sub routine performs the elastic scattering and direct reaction cross-section calculations within the framework of generalised optical model and coupled channel model. It is used for solving the coupled differential equations arising in the nuclear model calculations and also performs the parameter searches to fit calculated results to experimental data. The iteration technique searches for the one required solution among the many which are mathematically possible. The method supposes some ordering of the channels: first the ground state, then the state most strongly coupled to it. All channels must be coupled to some preceding one. The result of each iteration depends on this chosen order. If there is more than one equation related to the ground state the whole calculation must be repeated. The efficiency of the method is proportional to the ratio of the total number of equations to the number of those related to the ground state. The usual methods can also be used, but the iteration method is compulsory for spin-orbit deformation and Dirac formalism. The expression for the transmission coefficient is;

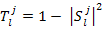(ii)

The S matrix elements, 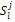are obtained by solving the differential equation for each partial wave. The calculations are done upto a point when S- matrix elements are sufficiently close to 1. For partial waves of large l, the scattering reduces to coulomb scattering.

These are simplified by eliminating the j dependence as;

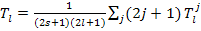(iii)

The level densities are calculated using the dynamic approach which takes into account collective enhancements of the level densities due to nuclear vibration and rotation. Below critical excitation energy, the superfluid model is used whereas above the critical excitation energy, Fermi gas model is used. This later one accounts for the rotation induced deformation of the nucleus, which becomes spin dependent [31]. This formulism explicitly accounts for the rotation induced deformation of the nucleus, which becomes spin dependent, The deformation of the nucleus is accounted for in the calculations through the moment of inertia and the level density parameter ‘a’ which increases with increase in the surface of the nucleus. For a prolate nuclei, assuming the axis of rotation to be perpendicular to the symmetric axix, the level density is expressed as

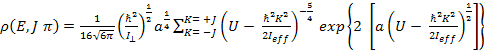(iv)

For oblate nuclei, where the axis of rotation is assumed parallel to the symmetric axis we have, the expression for level density given as;

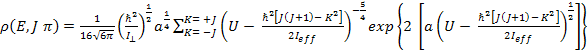(v)

Here ‘a’ is the level density parameter, J is the nuclear spin and K is its projection. U is related to the excitation energy E through the expression as;

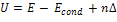(vi)

E_cond is the condensation energy given by;

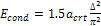(vii)

Δ is the pairing gap given as 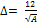, n is 1 for odd-odd nuclei, 2 for eveneven nuclei and zero otherwise. The effective moment of inertia Ieff is defined through the differences of inverses of I_┴ and I_‖ as;

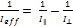(viii)

The statistical model code PACE4 is derived from the original code called JULIAN. It uses a Monte-Carlo procedure to determine the decay sequence of an excited nucleus using the Hauser-Feshbach formalism. The main advantage of Monte-Carlo calculations is to provide correlations between various quantities, such as particles and gamma-rays, or angular distribution of particles. Sequential decays are considered until any further decay is prohibited due to the energy and angular momentum conservation laws. A random number selection determines the actual final state to which the nucleus decays to and the process is, then repeated for other cascades until all the nuclei reach the ground state. The transmission coefficients for light particle emission (n, p, α) are determined using optical model potentials [32,33]. A fission decay mode is employed using a rotating liquid drop fission barrier routine. The code also provides event by event trace back of the entire decay sequence from the compound nucleus into any one of the exit channels. The fusion crosssections are obtained from the Bass model [34]. There are two default level density options that are essentially derived from the Fermi gas formalism and are identical to constant temperature formalism at low energies. These are i) the determination of the parameter ‘a’ and ii) ‘a’ is taken to be equal to A/K, where, A is the number of nucleons and K is constant factor. Independent of these options, rotational energy contribution Erot(J) can be selected in two ways viz., the spin cut-off parameter and the ground-state rotational energy of the finite-range rotating-drop model [35]. For values of A, Z or J beyond the range of validity of Sierk’s routine, the rotational energies are taken from the work of Cohen, Plasil and Swiatecki [36]. It has been observed that the code PACE4 is more accurate for high spins, close to the yrast line. The fission probability is calculated using the Bohr-Wheeler saddle point formalism [37]. The fission barriers are those of Sierk [35]. The code cannot be used for below barrier calculations. A special feature of the PACE4 code is its ability to provide information on energy and angular distributions of evaporated particles. This is obtained by tracking the distribution of projection through each cascade. The angular distribution of the emitted particles is determined at each stage of de-excitation. The code could be run with a large number of events (50,000) to obtain better statistics for the energy and angular distribution of residual nuclei.

The partial cross-section for CN formation at angular momentum (ℓ) and specific bombarding energy is given by,

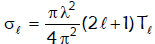(ix)

where, λ is the reduced wavelength and T_ℓ, the transmission coefficient given by,

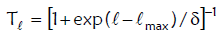(x)

where, δ is the diffuseness parameter and ℓ_max is determined by the total fusion cross-section σ_F, since,

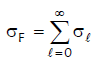(xi)

It may be pointed out that code PACE4 performs only the statistical equilibrium model calculations and does not take pre-equilibrium and incomplete fusion processes into consideration.

The TALYS code

The TALYS [38] code is designed for the analysis and prediction of nuclear reactions. It comprises of different nuclear models which have been well validated for simulation of nuclear reactions involving photons. Protons, neutrons, deuterons, tritons, ³He and alpha particles, ranging in energy from few KeV’s to 200 MeV. The target nuclei which can be studied are from mass number 19 and heavier.

TALYS uses the optical model code ECIS06 [39] for calculating the reaction cross-section, total cross-section, the shape elastic angular distribution, inelastic cross sections and angular distributions using either a coupled-channels (deformed nuclei) or DWBA (spherical nuclei) approach and the transmission coefficients, for compound nucleus decay and pre-equilibrium emission, The level densities are calculated using the back-shifted Fermi gas model for most of the nuclides and for some of the nuclides a combined Constant Temperature + Fermi gas model is used.

Results and Discussion

The Production cross-section of radio-isotopes; ^{149, 152, 155 &161}Tb have been evaluated via various reactions on the Gadolinium isotopes ^152,155&160Gd, using the theoretical codes EMPIRE 3.2 and PACE4 based on Hausher Feshback approach with the inclusion of TENDL-2019 library (calculated by TALYS code). Variation for all the calculated values of cross-section with respect to energy have been shown in Figures 1-4. It has been observed that the highest value of production cross-section for ¹⁴⁹Tb is around 520 mb, while with PACE code is 375 mb at incident proton energy of 42 MeV as can be seen from Figure 1, the production cross-section of ¹⁵²Tb by proton induced reaction on ¹⁵⁵Gd is given in Figure 2, the highest value of the production crosssection is found to be around 645 mb at proton incident energy of 38 MeV, similar result have been reported by experiment also [25,26]. The half- life of ¹⁵²Tb is 17.5 hours and the prominent decay modes are Electron capture and β+.The production of ¹⁵⁵Tb, is maximum at incident proton energy of around 12 MeV with cross-section to be around 500 mb as depicted in Figure 3, this is, quite a significant value as far as the production of the radioisotope is concerned. The half-life of the isotope is around 5.3 days, and the prominent decay mode is via EC (electron capture) thus makes it an important candidate for the therapeutic and diagnostic purposes in the medical industry mainly for SPECT, Moreover the isotope is also used to generate Auger electrons for therapy. The isotope ¹⁶¹Tb produced through ¹⁶¹Gd(p.γ)¹⁶¹Tb reaction has a maximum value of cross-section of around 55 mb at incident proton energy of 8 MeV, as is given in Figure 4. It may be pointed out that for the production of ^155&161Tb, no theoretical data has been observed through PACE4. The importance of the present calculations further increases keeping in view the scarcity of the experimental results. It may further aid to open up the new experimental opportunities for the production of this radionuclide (Figures 1-4).

The production of radionuclides ^{149, 152, 155 & 161}Tb is of significant importance considering their use in nuclear medicine, which decays primarily through electron capture and positron emission, thus a potential candidate for PET and SPECT. The present work describes a direct production route of the radionuclides ^{149, 152, 155 & 161}Tb which otherwise is not generally available. The results can be studied to design new production pathway for the radionuclides ^{149, 152, 155 & 161}Tb.

Acknowledgements

D. P. Singh thanks to SERB-DST for providing financial support through Project No. ECR / 2017 / 000641 under the early Career Research Award. Support from University of Petroleum & Energy Studies (UPES), Dehradun for conducting this work is gratefully acknowledged.

References

1. Winsberg, Lester. "Recoil Studies of Nuclear Reactions Induced by High-Energy Particles, I. Production of Tb 149." Phys Rev 135 (1964): B1105.
2. https://pubs.rsna.org/doi/abs/10.1148/radiology.207.1.90?journalCode=radiology
3. https://www.wiley.com/en-us/Radiation+Detection+and+Measurement%2C+4th+Edition-p-9780470131480
4. Knapp, Furn F., and Ashutosh Dash. “Radiopharmaceuticals for therapy”. New Delhi, India, Springer 2016.
5. S.M. Seidlin, L.D. Martinelli, and E. Oshry. “Radioactive iodine therapy: Effect on functioning metastases of adenocarcinoma of the thyroid”. JAMA 132.14:838–847, 1946.
6. http://www.nupecc.org/pub/impact_applications_1994.pdf
7. Yiğit, M., and E. Tel. "Nuclear model calculation for production of 18F, 22Na, 44, 46Sc, 54Mn, 64Cu, 68Ga, 76Br and 90Y radionuclides used in medical applications." Ann Nucl Energy 69 (2014): 44-50.
8. Crasta, Rita, H. Naik, S. Suryanarayana and P. Prajapati et al. "Photo-neutron cross-section of 100Mo." J Radioanaltical Nuclear Chemistry 290 (2011): 367-373.
9. Büyükuslu, H., Abdullah Kaplan, G. Yıldırım and A. Aydin et al. "Production cross sections of medical 110,111 In radionuclides." Kerntechnik 75 (2010): 103-108.
10. Mushtaq, A. "Producing radioisotopes in power reactors." J Radioanal Nucl Chem 292 (2012): 793-802.
11. https://inis.iaea.org/search/search.aspx?orig_q=RN:24057124
12. Aydin, A., B. Şarer, and E. Tel. "New calculation of excitation functions of proton-induced reactions in some medical isotopes of Cu, Zn and Ga." Appl Radiat Isot (2007): 365-370.
13. Tel, Eyyüp, Mustafa Yiğit, and G. Tanır. "Study on (n, t) reactions of Zr, Nb and Ta nuclei." J. Fusion Energy 31 (2012): 184-190.
14. Tel, Eyyüp, Mustafa Yiğit, and G. Tanır. "Cross sections calculations of (d, t) nuclear reactions up to 50 MeV." J. Fusion Energy 32 (2013): 273-277.
15. Yiğit, Mustafa, and Eyyüp Tel. "Alpha production cross sections for some target fusion structural materials up to 35 MeV." J Fusion Energy 32 (2013): 442-450.
16. Yiğit, M., E. Tel, and A. Kara. "Deuteron Induced (d, p) and (d, 2p) Nuclear Reactions up to 50 MeV." J Fusion Energy 32 (2013): 362-370.
17. Ditroi, Fenyvesy., Ferenc Tárkányi, Sandor Takacs and Alex Hermanne et al. "Investigation deuteron-induced reactions on cobalt." Nucl Instrum Methods Phys Res B 268 (2010): 2571-2577.
18. Herman, M., R. Capote, B. V. Carlson and P. Obložinský et al. "EMPIRE: nuclear reaction model code system for data evaluation." Nucl. Data Sheets 108 (2007): 2655-2715.
19. Gavron, A. "Statistical model calculations in heavy ion reactions." Phys Review C 21 (1980): 230.
20. Koning, A. J., D. Rochman, J-Ch Sublet and N. Dzysiuk et al. "TENDL: complete nuclear data library for innovative nuclear science and technology." Nucl Data Sheets 155 (2019): 1-55.
21. Müller, Cristina, Konstantin Zhernosekov, Ulli Köster and Karl Johnston et al. "A unique matched quadruplet of terbium radioisotopes for PET and SPECT and for α-and β−-radionuclide therapy: an in vivo proof-of-concept study with a new receptor-targeted folate derivative." J Nucl Med 53 (2012): 1951-1959.
22. https://www.nap.edu/catalog/11985/advancing-nuclear-medicine-through-innovation
23. dos Santos Augusto R, Buehler L, Lawson Z and Marzari S et al, CERN-MEDICIS collaboration 4 (2014):265–281.
24. Steyn, G. F., C. Vermeulen, Ferenc Szelecsényi and Z. Kovács et al. "Cross sections of proton-induced reactions on 152Gd, 155Gd and 159Tb with emphasis on the production of selected Tb radionuclides." Nucl Instrum Methods Phys Res B. 319 (2014): 128-140.
25. Müller, Cristina, Konstantin Zhernosekov, Ulli Köster and Karl Johnston et al. "A unique matched quadruplet of terbium radioisotopes for PET and SPECT and for α-and β−-radionuclide therapy: an in vivo proof-of-concept study with a new receptor-targeted folate derivative." J Nucl Med 53 (2012): 1951-1959.
26. Müller, Cristina, Christiaan Vermeulen, Ulli Köster and Karl Johnston et al. "Alpha-PET with terbium-149: evidence and perspectives for radiotheragnostics." EJNMMI Radiopharm Chem 1 (2017): 1-5.
27. Ku, Anthony, Valerie J. Facca, Zhongli Cai, and Raymond M. Reilly. "Auger electrons for cancer therapy–a review." EJNMMI Radiopharm Chem 4 (2019): 1-36.
28. https://inis.iaea.org/search/search.aspx?orig_q=RN:29067412
29. Hauser, Walter, and Herman Feshbach. "The inelastic scattering of neutrons." Physi Revi 87 (1952): 366.
30. https://inis.iaea.org/collection/NCLCollectionStore/_Public/04/059/4059477.pdf
31. Vigdor, S. E., and H. J. Karwowski. "Influence of deformed-nucleus level densities on statistical model calculations for high-spin fission." Physi Revi C 26 (1982): 1068.
32. Perey CM, Perey FG. Compilation of phenomenological optical-model parameters 1954–1975. Atomic data and nuclear data tables. 17(1976):1.
33. Huizenga, J. R., and George Igo. "Theoretical reaction cross sections for alpha particles with an optical model." Nucl Phys 29 (1962): 462-473.
34. Bass, R. "Nucleus-nucleus potential deduced from experimental fusion cross sections." Phys Rev Lett 39 (1977): 265.
35. Sierk, Arnold J. "Macroscopic model of rotating nuclei." Physical Review C 33 (1986): 2039.
36. Cohen, S., F. Plasil, and W. J. Swiatecki. "Equilibrium configurations of rotating charged or gravitating liquid masses with surface tension. II." Ann Phys 82 (1974): 557-596.
37. Bohr, Niels, and John Archibald Wheeler. "The mechanism of nuclear fission." Physical Review 56 (1939): 426.
38. Koning, Arjan J., Stephane Hilaire, and M. C. Duijvestijn. "TALYS-1.0." In International Conference on Nuclear Data for Science and Technology (2007): 211-214.
39. https://link.springer.com/article/10.1140/epja/s10050-021-00596-4