Perspective - (2023) Volume 17, Issue 3
Received: 21-May-2023, Manuscript No. glta-23-105736;
Editor assigned: 22-May-2023, Pre QC No. P-105736;
Reviewed: 13-Jun-2023, QC No. Q-105736;
Revised: 19-Jun-2023, Manuscript No. R-105736;
Published:
26-Jun-2023
, DOI: 10.37421/1736-4337.2023.17.390
Citation: Yoon, Hyesun. “Generalized Connections, Stokes' Theorem and the Abelian Chern–Simons Theory.” J Generalized Lie Theory App 17 (2023): 390.
Copyright: © 2023 Yoon H. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Summed up associations and their math have been created with regards to quantum gravity. They are applied to abelian Chern–Simons theory in this case. Utilizing flux operators, generalized connections and Stokes' theorem, we determine the expectation values of holonomies in U(1) Chern–Simons theory. An outlining of the holonomy circles emerges in our development and we show how, by picking normal framings, the subsequent assumption esteems by and by characterize a useful over check invariant round and hollow capabilities [1].
Stokes' theorem
Stokes' theorem is a fundamental result in vector calculus that relates the integral of a vector field over a surface to the circulation of the vector field around the boundary of that surface. It is a higher-dimensional extension of the fundamental theorem of calculus and plays a crucial role in many areas of mathematics and physics.
Statement of stokes' theorem
Let S be an oriented, smooth and bounded surface in three-dimensional space and let ∂S be its positively oriented boundary curve. If F is a vector field that is continuously differentiable in a region containing S, then Stokes' theorem states:
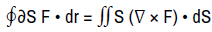
where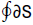 
denotes the circulation or line integral around the boundary curve ∂S,
F • dr represents the dot product of the vector field F with the differential vector
element dr along the curve, 
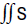denotes the surface integral over the surface S,
(∇ × F) is the curl of the vector field F and dS represents the differential vector
element of surface area on S.
We'll take a different route here. We will give a deduction of the assumption values, utilizing procedures connected with summed up associations. Utilizing Stokes' theorem, the goal is to substitute (exponentials of) integrals of the curvature over surfaces with the holonomy loops serving as boundaries for holonomies under the path integral. The curvature of the connection is then obtained by making use of the Chern–Simons theory feature that the action's functional derivative with respect to the connection. Thus, functional derivatives can be used to replace the aforementioned curvature integrals below the path integral. Finally, we find that these functional derivatives are well-defined entities that can be evaluated to produce the desired expectation values and are referred to as flux operators in the literature on loop quantum gravity. On the specialized level, it is an association among inking and crossing point numbers noticed a long while prior that prompts the presence of the connecting numbers in the outcome [2].
Interpretation and implications
Stokes' theorem provides a deep connection between the circulation of a vector field around a closed curve and the flux of the curl of the vector field across the corresponding surface. It demonstrates how local properties of the vector field, as captured by its curl, relate to global properties of the field, as represented by the circulation and the surface integral.
The theorem has broad applications in various areas of physics and mathematics. In fluid dynamics, Stokes' theorem relates the circulation of a fluid velocity field around a closed loop to the vorticity within the enclosed region. In electromagnetism, it connects the electromotive force along a closed loop to the magnetic field's rate of change enclosed by the loop. Stokes' theorem is also essential in differential geometry and differential forms, forming the foundation of the exterior calculus framework [3].
Generalized connections
In mathematics, generalized connections refer to extensions of the concept of connections from differential geometry to more general settings, such as fiber bundles, gauge theories and noncommutative geometry. A connection provides a way to differentiate objects along a manifold or space and captures the concept of parallel transport. Generalized connections encompass a wide range of mathematical structures and have applications in various fields. For example, in gauge theory, connections describe the interactions between particles and gauge fields. In fiber bundles, connections allow for the study of differentiation and parallel transport of objects over a base space. In noncommutative geometry, connections provide a framework for understanding differential calculus on noncommutative spaces [4].
The study of generalized connections involves developing appropriate mathematical structures and defining their properties and transformations. It requires a deep understanding of the underlying mathematical framework and its applications in specific contexts. This is necessary to make the analog of the commutator well defined for non-abelian groups, so that there are only a finite number of transversal intersections for all pairs of compact loops and surfaces. This is anyway not a worry for the work introduced here, since due to the abelian idea of transition administrators are distinct even on circles that cross the hidden surface limitlessly frequently as long as the Gauss connecting between the circle and the limit of the surface is limited. This is the situation assuming that we work with piecewise scientific circles and limits.
Stokes' theorem is a fundamental result in vector calculus that establishes a relationship between the circulation of a vector field around a closed curve and the flux of the curl of the vector field across the corresponding surface. It has broad applications in physics and mathematics, providing insights into fluid dynamics, electromagnetism and differential geometry. Generalized connections, on the other hand, extend the concept of connections to more general mathematical structures and play a vital role in areas such as gauge theories, fiber bundles and noncommutative geometry [5].
Both concepts contribute to our understanding of mathematical structures and their applications in diverse fields. Seifert surfaces remain evident in this instance and the concept of a compressing disc can be trivially extended to include a piecewise analytic boundary. Finally, it is clear that all properties have not changed. In this manner, in the fundamental text, we will constantly expect circles to be piecewise logical and surfaces to be smooth.
None.
No conflict of interest.
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
