Irradiation effect Predictions in MgO using Molecular Dynamics Simulations of Incident Single and Multiple Au Ions

Mohamed S. El-Genk^2* and Benjamin J. Cowen^1
*Correspondence: Mohamed S. El-Genk, Nuclear Engineering Department, University of New Mexico, USA, Email:

Keywords

• MD simulations • MgO • Defect clusters and cascades • Threshold displacement energy • Ballistic melting • Single and multiple Au ions • Residual defect clusters • Vacancies interstitials

Introduction

Atomistic simulations are useful for identifying potential mechanisms associated with the production and evolution of defects in materials during irradiation by incident ions and neutrons in many applications. The simulation results could help improve the predictions of multi scale models of radiation damage in materials [1]. Predictions of radiation damage in metal oxides and carbides are of timely interest for the development of next generation nuclear reactors, such as high temperature gas cooled reactors, sodium cooled fast reactors, molten salt cooled reactors, molten lead and lead bismuth cooled reactors, and accident tolerant fuel systems. In these applications, the effects of irradiation on the reactor vessel, cladding, and fuel materials need to be investigated and characterized [2-9]. Metal oxides, such as Al₂O₃, Cr₂O₃, Y₂O₃, and MgO, in the form of additives, nanoparticles, or coatings, have been used to increase the strength and the radiation hardness of structural materials in nuclear reactors [3,9-13]. For example, carbides such as 3C-SiC and amorphous SiC (a-SiC), are being investigated in the development of accident tolerant fuel systems in current and next generation light water reactors (LWRs), as well as for use in the plasma facing blankets of fusion reactors [14-18].

The accumulation of vacancies and interstitials in metal oxides could cause a crystalline to amorphous phase transition [2,19,20]. In order to alleviate or moderate these effects at the nominal operating temperatures in nuclear reactors, it is desirable to choose materials in which irradiation induced interstitials are significantly more mobile than the vacancies. Consequently, the vacancy rich regions could function as recombination centers, reducing irradiation effects. Materials of low vacancy mobility, over the range of operating temperatures of interest in nuclear reactors, include 3C-SiC and MgO [2]. However, the investigations of irradiation effects in SiC are more mature and abundant than of MgO and MgO based composites, which is a focus of this work.

One of the most popular tools for investigating radiation effects in materials at the atomistic scale is molecular dynamics (MD) simulations. They employ applicable interatomic potentials to model atom atom interactions. MD simulations have been used to determine the probability distributions of the threshold displacement energies (TDEs) for use in radiation damage predictive models [16,21-24], and track irradiation induced defect clusters, and the extent of the produced defect cascades over picosecond (ps)- nanosecond (ns) time scales. The extent of defect cascades and the size of defect clusters produced depend on the total energy and the fluence of incident particles [16,21,22,25-28].

Uberuagu et al. [29,30] have used MD simulations with single PKAs, of energies up to 5 keV, to investigate the mobility of the defects produced defects in MgO. They observed the production of point defects and small defect clusters and indicated that the vacancies were immobile at room temperature. As a result, mobile interstitials either cluster with others or recombine with some of the vacancies in the vicinity. They hypothesized that some of the interstitial clusters would be stable over a time frame of years. Another study of radiation effects in MgO by Trachenko et al. [31] using MD simulation, tracked defect production by an incident 40 keV uranium atom. Results showed that MgO was resistant to ballistic melting, and only residual point defects and small defect clusters were formed.

Due to the computational limitations of modeling radiation effects of high energy incident particles in materials, particularly during the ballistic phase of interaction, an alternative approach has been developed for investigating the production and the evolution of defects in MgO. Aidhy et al. [32] have used MD simulations to investigate the annealing of produced defects by irradiation on both sublattices in MgO. They inserted Frenkel pairs into a previously equilibrated system of atoms of target material. This approach bypasses the computationally expensive ballistic phase of interaction and creates systems rich in defect concentrations. While artificially introduced defects can provide insight into the formation of different defect clusters and structures, those forming by overlapping damage cascades could be entirely different.

The applicability of MD simulations using single incident particles or PKAs of only a few keV is limited, Materials of interest would be exposed to fluxes of incident particles of varying energies and directions. Depositing hundreds of keV with multiple incident particles in the crystal lattice of the target material could produce large defect clusters not possible to produce or observe using a single incident particle of the same total energy. Therefore, investigating the production and the evolution of the defect clusters by multiple incident particles would be useful. Results would more realistically quantify the effects of radiation in the materials of interest. This issue is addressed by the work presented in this paper.

The objectives are to perform MD simulations using high energy, single and multiple incident Au ions to investigate the irradiation effect on the production and extent of defect cascades in crystalline MgO. The directional dependence of the TDE for the formation of stable Frenkel pairs and for the displacement of an atom are calculated. In addition, the obtained probability distributions, averaged over all crystallographic directions, for PKAs with energies up to 400 eV, are compared. The single incident Au ions investigated in the present MD simulations have energies of 5, 10, 20, and 50 keV. The obtained results are compared to those using 5 and 10 incident Au ions of 5, 10, and 20 keV each. In all simulations with multiple incident ions, the formation and evolution of the defect cascades during the ballistic and annealing phases of interactions are determined and compared. The possibility of ballistic melting of MgO is also investigated using simulated selected area electron diffraction (SAED) patterns and radial distribution functions (RDFs).

Methodology

The present MD simulations of radiation effects of single and multiple incident Au ions in MgO are carried out using the Large scale Atomic/ Molecular Massively Parallel Simulator (LAMMPS) [33]. The simulations employ a splined Buckingham interatomic potential to model atom atom interactions. This potential, also used by Uberuagu et al. [29] to model radiation damage in MgO, is based off the parameterizations of Lewis and Catlow [34]. The Buckingham potential is expressed as:(1)

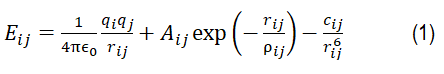
Where E_ij is the energy between the i_th and j_th particles, q_i and q_j are the atom charges, r_ij is the distance between atoms, and A_ij, ρ_ij, and C_ij are fitted parameters. To account for the short range interactions, the Buckingham potential (Eq. 1) is smoothly splined at short interatomic distances to the ZBL potential, expressed as:

where e is the electron charge, S is a switching function, Z_i and Z_j are the nuclear charges of the atoms, ϵ_o is the vacuum permittivity, and ϕ(r_ij/a) (2)

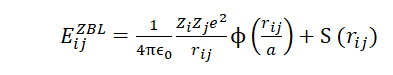
is an exponential function. The exponential spline to smoothly transition the Buckingham potential to the ZBL potential at short interatomic distances is expressed as: (3)

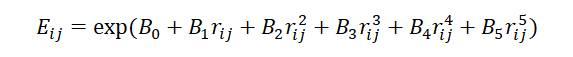
The splined Buckingham+ZBL potential for O-O and O-Mg interactions are shown in Figure 1. Both the first and second derivatives of the splined potentials are smooth and continuous. Note that the Mg-Mg interactions are excluded since A_ij, ρ_ij, and C_ij in Eq. (1) are 0 and the Buckingham interactions are ignored. All Coulomb interactions are modeled using the particle particle particle mesh (PPPM) solver, with a relative error of 1.0 ×10^-6.

In order to estimate the directional dependence and probability distributions of the TDEs for MgO, the employed system of 21,952 atoms in the simulations first used the Polak Ribiere version of the conjugate gradient algorithm [35] to perform energy minimization of the atoms. Subsequently, the system of atoms is equilibrated first in an isothermal isobaric ensemble (NPT) for 100 ps, then in a microcanonical ensemble, with a thermostatic boundary layer (NVE), for an additional 100 ps. The thermostatic boundary layer allows for the physical dissipation of deposited energy in the system to the bulk material.

The simulations to calculate the TDEs used a total of five O and five Mg PKAs in 23 crystallographic directions, and with increased energy from 1.0 to 400 eV, in increments of 1 eV. The simulations employ a variable time step algorithm, such that no atom moves more than 0.005 Å per time step. The calculated TDE probability distributions for the displacement of an atom are averaged over all crystallographic directions. The simulations continued for 10 ps before determining the effects of the PKA energy and type on the crystal lattice.

In the simulations with single and multiple incident Au ions, the MgO system comprised of 27,648,000 atoms is periodic in the x and y directions and fixed in the z direction. This system also used the Polak Ribiere [35] version of the conjugate gradient algorithm to perform the energy minimization of the atoms. Before starting the simulations, this system of atoms is equilibrated using an NPT ensemble for 500 ps and then using an NVE ensemble for 30 ps. A thermostatic boundary layer that is 10 Å thick is applied at the periodic boundaries of the system, and the same variable time step algorithm used in the TDE simulations is employed.

The performed simulations investigated irradiation effects by single incident Au ions, with energies ranging from 5 to 50 keV, both in the (001̅) direction and normal to all faces of the MgO crystal, which is a <100> family direction. Additional simulations are carried out using 5 and 10 incident Au ions and the obtained results are compared to those of single incident ions. Although the multiple incident ions enter the simulation domain simultaneously, they are not explicitly descriptive of a real world experiment. However, they help investigate the production and the evolution of larger defect structures, which is not impossible using conventional simulations with single incident ions or PKAs. The present investigation with multiple incident ions uses a non-traditional technique, It is similar to the work by Aidhy et al. [32] in which they inserted Frenkel pairs into the system to bypass the lengthy and costly computation associated with the simulation of ballistic phase of interaction. Instead, the present simulations include the ballistic phase of interactions with multiple incident heavy Au ions, to investigate the production and evolution of large defect structures, which are not studied previously.

The present investigations used Wigner Seitz (WS) defect analysis to determine and track the number and type of produced vacancies, interstitials, and antisites during both the ballistic and the annealing phases of interaction. Note that “annealing” in the present work refers to the immediate recombination of the produced interstitials and vacancies, rather than the definition of “slow cooling” used in metals and alloys processing. The Open Visualization Tool (OVITO) [36], and its customizable python scripting interface are used to determine the produced clusters of vacancies and interstitials, The lattice parameter was the cutoff for counting defects in the same cluster. RDFs and simulated SAED patterns of the defects production region are used to identify the changes in the crystal lattice. The SAED patterns are obtained by calculating the electron diffraction intensity on a mesh of reciprocal lattice nodes [37]. The visualization is carried out by taking the logarithm of the diffraction intensity in Paraview [38].

Results and Discussion

The results of the MD simulations to determine the directional dependence of Frenkel pair formation and the displacement of an atom are first presented and discussed. Subsequently, the obtained TDE probability distributions for the displacement of an atom by Mg and O PKAs are presented. The simulation results of the produced defect clusters and cascades in crystalline MgO, using single projectiles with energies up 50 keV, and 5 and 10 projectiles with a fluence of 5/nm2 and energies up to 20 keV, are also presented and compared. These results include the number and type of point defects produced at the peak of the ballistic phase and the residuals, defect clustering, and extent of the defect cascade. The obtained SAED patterns and RDFs of the MD simulation results are used to identify the induced changes in crystallinity of the MgO, as a function of the number and energy of incident Au projectiles.

Threshold displacement energy

The reported TDE values for the same materials in the literature vary, depending on the simulation method and interatomic potential, used and the applied definition. One defines TDE as the lowest energy required to permanently displace the PKA. However, since PKAs sometime recoils to their original lattice sites and in the process produces stable point defects, this definition is not fully appropriate for identifying actual damage to the crystal lattice. The second defines TDE as the lowest energy to produce a stable Frenkel pair. A third definition is the lowest energy for the displacement of an atom on any sublattice [22]. Table 1 lists the lowest energies calculated for the production of an oxygen or magnesium vacancy and the displacement of an atom by O and Mg PKAs.

In the present simulations for MgO, defect production near the threshold energies is typically limited to the sublattice of the PKA, which is in agress with prior work [39]. However, this is not always the case for all 23 crystallographic directions investigated herein. For instance, in the (100) direction, the lowest energy for an O PKA to produce an oxygen vacancy is 159 eV, compared to 86 eV to produce a magnesium vacancy. This is because in the (100) direction, the O PKA collides directly with Mg secondary knock on atom (SKA) and recoils back to its initial lattice site. At high enough energy (86 eV), the Mg SKA is displaced and becomes an interstitial. When an O PKA has enough energy to become permanently displaced, it causes a replacement collision sequence with the Mg SKA.

The PKA energy for displacement is sometimes lower than that for the formation of a stable vacancy (Table 1). This is because a displaced atom can swap places with another atom, and thus resides at a different lattice site. In all crystallographic directions investigated, the (122) and (233), showed the energy for displacing an O PKA is identical to that for forming a stable vacancy. With Mg PKAs, the crystallographic directions with lower PKA energies for a displacement are lower than for the formation of stable vacancies are (123), (015), (025), (012), (122), (233), and (566). However, the difference is usually a few eV, but can be up to 15 eV, as in the (566) crystallographic direction with Mg PKAs. These differences quantify the dependence of the TDE values on the crystallographic direction. Therefore, owing to the stochastic nature of radiation damage in target materials, the lowest energy to cause a displacement may not be used as input into binary collision approximation models for predicting radiation damage in materials. Instead, a probability distribution that is averaged for all crystallographic direction would be more representative of the defects production. The calculated TDE probability distributions for the displacement of an atom by Mg and O PKAs are compared in Figure 2. In this figure, the TDEs corresponding to a 50% displacement probability are 94 and 91 eV for the O and Mg PKAs reported by Park et al., [39] of 90 ± 2 eV.

Figure 3 presents images of the produced defect cascades in MgO by single incident Au ions with energies of 5, 10, 20, and 50 keV. The extent of these cascades increases from 5.7 nm to 35.6 nm, as the energy the incident ion increases from 5 to 20 keV. All cascades are contained within the simulation box of over 27 million atoms (Figure 3), except that for the 50 keV Au3+ with an angle of incidence in the (001̅) direction, which channeled through the entire simulation domain. This incident ion loses 64% of its energy as it channels through 100 nm of MgO, primarily producing point defects, such as vacancies and interstitials. For the incident ion energies in Figure 3, the produced defect cascades spread out throughout the entire simulation domain, with no or little defect clustering. However, some sputtering at the back face occurs as the incident Au ion exits the simulation box.

Figure 4 presents the number and types of point defects produced as a functions of the energy and number of Au projectiles, during the ballistic and annealing phases of interaction. The number of produced interstitials, vacancies, and antisites produced on both sublattices is similar. This is consistent with the calculated TDEs, which are nearly identical for both PKA types (Table 1). Results show that the number of residual point defects always increases as the number of incident ions increases, regardless of the ion energy. However, the extent of the defect cascade depends on the total energy of the incident ions. Results also indicate that for the same total energy deposited, increasing the number of incident ions causes more damage than increasing their energies. For example, ≈2,000 residual oxygen vacancies are produced in the simulation with 10, 10-keV incident Au ions, compared to only ≈160 oxygen vacancies in the simulation with 5, 20-keV incident Au ions. Although the total energy introduced into the system in both cases is the same (100 keV), increasing the number of incident ions produces more stable and larger defect clusters. The residual defects produced by 10 5-keV incident Au ions is approximately an order of magnitude higher than those produced with 5 20-keV Au ions. These results are true for all energies and number of the incident Au ions investigated.

In the present simulations, the large number of antisites produced during the ballistic phase of interaction is partially caused by the elastic deformation of the crystal lattice, rather than by an irreversible inelastic deformation. An elastic wave of deformation (Figure 5) propagates away from the impact region of the incident ions to the thermostatic boundary layer of the system. Figure 5 presents top views of the produced defect clusters and cascades produced in the MgO crystal by 1, 5, and 10 20- keV incident Au ions at the peak of the ballistic phase of interaction and of the residuals after annealing. At the peak of the ballistic phase, the projected area of the produced defect cluster produced by 1, 5, and 10, 20- keV incident Au ions is 1.95, 8.64, and 65.9 nm², respectively. These areas decrease after annealing to 0.94 nm², 5.9 nm², and 44.0 nm², respectively.

The results in Figure 6 show that the energy of the incident Au ions also impacts the projected areas of the produced defect cascades. With 10 incident ions of 5, 10, and 20 keV each, the areas of the produced defect cascades are 21.6, 61.4, and 65.9 nm², respectively. After annealing these areas, which are much larger than those shown in Figure 5, decrease to 13.7, 35.8, and 43.9 nm², respectively.

Figure 7 shows a close up view of significant sputtering and swelling produced at the MgO surface by 10 20-keV incident Au ions, at the peak of the ballistic phase of interaction. A total of 169 atoms are sputtered off the surface, compared to 171 atoms by the 10 10-keV incident Au ions, and 40 by the 10 5-keV Au ions.

Figure 8 compares the images of the produced clusters and cascades of vacancies and interstitials, at the peak of the ballistic phase and after annealing (residuals), by 5 incident Au ions of 5, 10, and 20 keV each. At the peak of the ballistic phase of interaction, significant defects are produced below the surface, and the size and extent of the defect cascade increases as the energy of the incident ions increases. In addition, the atoms are knocked out of a central core region of the target MgO system produce a large cluster of vacancies whose size increases with increased energy of incident ions. The outer edge of this cluster is populated with interstitials, which are much more mobile than the vacancies. Immediately beyond the peak of ballistic phase, a significant number of the produced defects anneal by recombination of the vacancies and interstitials, significantly decreasing the size of the defect clusters. However, some residual defects and defect clusters remain after annealing.

In Figure 8, the vacancy rich regions are easily identified by the relative concentrations of light and dark blue atoms representing the oxygen and magnesium vacancies. To magnify the images of the defect clusters, the entire defect cascades produced by the 5 20-keV incident Au ions are not shown in Figure 8. Another reason is that the defect cascade produced by one of the incident ions extends as much as ≈74 nm from the surface, while those produced by the other 4 ions extended only ≈20 nm.

Increasing the number and energy of the incident ions significantly increases not only the size of the defect clusters, but also the extent of the defect cascade produced in the MgO target. Figure 9 compares the images of the clusters and cascades of vacancies and interstitials produced by 10 incident Au ions of 5, 10, and 20 keV at the peak of the ballistic phase and after annealing (residuals). The individual vacancies and interstitials in the images in Figure 8 and Figure 9 are identified using WS defect analysis. It is interesting to note that the images of the produced defect clusters near the surface experiences necking several nanometers below the surface. This suggests that the defect cluster produced close to the surface by the incident ions tends to spread outward while the bulk of the incident ions’ energy is deposited below the necking region, producing a large defect cluster. After annealing, different but much smaller clusters of vacancies and interstitials remain in the material. In each case, there are residual clusters of vacancies and interstitials larger than the rest.

The results in Figure 9 show a residual cluster of vacancies, identified by the light and dark blue atoms, and a large nearby residual cluster of interstitials. The cluster of vacancies starts at the surface and extends just beyond the necking region, and the cluster of interstitials forms directly below the surface (Figures 9d-f). While most of the produced defects in the ballistic phase of interaction anneal, the formation of large and stable cluster of residual interstitials precludes the thermal recombination in the vacancy rich region. However, at high temperatures, some of the produced interstitials would annihilate as the immobile vacancies act as recombination centers.

Figure 10 compares the number of vacancies in the largest cluster produced in MgO by different numbers of incident Au ions, (1, 5 and 10) of different energies (5, 10, and 20 keV), as a function of simulation time, including the ballistic and annealing phases of interactions. The results in this figure show a distinct dependence of the number of vacancies produced on the number of incident ions and to a lesser extent on their energy. For instance, the number of the produced vacancies in the largest cluster by single incident ions with energies of 5, 10 and 20 keV at the peak of the ballistic phase is 313, 319, and 354, respectively. After annealing these numbers decrease by more than an order of magnitude to only 7, 14, and 14, respectively. With multiple incident ions, the number of vacancies produced, and the size of the defects cluster increases significantly. For example, the largest clusters of vacancies produced at the peak of the ballistic phase by 10 incident Au ions of 5, 10, and 20 keV, have ≈14,800, 38,400, and 102,500 vacancies, respectively. These numbers decrease after annealing to ≈1,900, 4,000, and 5,000, respectively. The large increases in the number of vacancies produced by multiple incident ions, is due in part to the overlapping of the defect cascades produced by the individual ions. The increase in defect production impacts the morphology of the system of atoms in the simulations. The vacancy rich regions cause density inhomogeneity and provide fast diffusion pathways. This is consistent with the reported observations for zirconium silicate and titania, based on the results of MD simulations and X-ray scattering [40,41].

Figure 11 shows a similar trend to that in Figure 10, for the largest clusters of interstitials produced at the peak of the ballistic phase, and after annealing, by incident ions of 5, 10, and 20 keV each. In Figure 10 and Figure 11, the interstitials clusters are smaller than those of the vacancies for three reasons: (1) some vacancies are caused by atom sputtering at the surface by incident Au ions; (2) the interstitial sites are identified using WS defect analysis, and the performed cluster analysis groups these sites, but do not account for the possibility that there could be more than one interstitial at a given site; (3) the produced vacancies in MgO are practically immobile, while the interstitials are highly mobile. This creates a vacancies rich cluster and displaces most interstitials to the outer region of the defects clusters.

Tracking the evolution of defect production and clustering in MgO provides valuable information on the induced changes in the target system of atoms. The SAED patterns in Figure 12 of unirradiated MgO (periclase) in the zone axes of (100), (110), and (111) shows clear diffraction peaks in the monocrystalline MgO. These SAED patterns are compared to those obtained of MgO after irradiation with Au ions (Figures 13-15). The SAED patterns presented in these figures are of the defect production by 5, 10, and 20 keV single and multiple Au ions at the peak of the ballistic phase and after annealing. Note that for the irradiated SAED patterns, only the (111) zone axis is shown, and the defect production region sampled is 40 nm3 in size. This size of the defect production region avoids finite size effects in the calculation of the simulated SAED pattern.

Figures 13-15 show that ballistic melting of MgO in the defect production region is unlikely to occur by single incident Au ions, regardless of their energy (Figures 13b, d, f). Conversely, the SAED pattern of the defect production region by multiple incident Au ions of 5 keV suggests the presence of ballistic melting at the peak of the ballistic phase of interaction (Figure 14a, c, e). The 5 keV multiple incident ions cause intense local defects production, while the defects produced by the 10 and 20 keV ions are more spread out. The produced defects by the 5 keV multiple ions are more localized to a single region because the ions do not travel far from the impinged surface. Nonetheless, with 10 incident Au ions, ballistic melting is more prominent (Figures 15a, c, e). After annealing, crystallinity is mostly retained for all single and 5 incident ions strikes, as demonstrated by the simulated SAED patterns presented in Figures 13b, d, f and Figures 14b, d, f.

The MD simulation results of 10 incident ions of varying energies, show extensive ballistic melting at the peak of the ballistic phase of interaction. The diffraction peaks corresponding to the unirradiated crystal are only faintly visible in the simulation results with 10 5-keV Au ions, and unnoticeable in the results of the simulations with 10 10-keV and 10 20- keV Au ions. This is in agreement with the WS defect analysis and the cluster analysis, which show a large defect cascade disrupting the entire crystal lattice along the path of the incident Au ions. The diffraction peaks are visible after annealing for all energies of the10 Au ions, however, there is still measurable disorder. The intensity of the residual disorder in MgO increases with increased energy of the incident ions (Figures 15b, d, f). The SAED patterns in these figures show that after annealing there are small and pockets of crystalline disorder within the residual defects clusters.

The present results of the simulated SAED patterns are consistent with the RDFs of the defect production region (Figure 16). At the peak of the ballistic phase of interaction by 10 20-keV incident ions, g (r)→1 at ≈ 3 Å, confirming the complete loss of the crystalline order. The initial peak and subsequent stabilization are indicative of an amorphous material, which still has short range order. After annealing, the peaks in the RDF reappears for all cases investigated, but are not as sharp and distinct. With 1, 5, and 10 20 keV incident Au ions, the half width of the first peak in the RDF at the peak of the ballistic phase of interaction is 0.2, 0.4, and 0.61, respectively. Thus, the amount of disorder produced increases as the number of incident ions increases, in agreement with the results of the simulated SAED patterns (Figures 13-15).

Figure 17 and Figure 18 show cross-sectional views of the MgO lattice in the simulations with 10 incident Au ions of 5, 10, and 20 keV each, both at the peak of the ballistic phase of interaction and after annealing. The images in Figure 17 color code the atoms based on their displacement distance. Atoms colored blue are not been displaced, while those displaced by ≥10 Å are colored red. The images in Figure 18, however, color code the atoms based on their type.

The images in Figure 17 indicate that the target atoms are permanently displaced tens of nanometers below the surface, while those in Figure 18 show significant recovery after annealing due to the recombination of the defects produced during the ballistic phase. The residual defects exist primarily near the surface. The color coded images show that displaced atoms exist further below the surface, where the system regains crystallinity. The images in Figure 18 show the presence of residual amorphous pockets, which is consistent with the simulated SAED patterns in Figure 15. At the peak of the ballistic phase, the sputtering and upswelling caused by incident ions are clearly shown in all the images in Figure 17. The residual damage to the surface is also indicated in these images showing random arrangements of the atoms that extends below the surface.

In summary, the results of the present simulations show that the produced vacancy rich regions in MgO are stable over tens of picoseconds and could act as recombination centers for the mobile interstitials. While ballistic melting occurs with 10 10-keV and 20-keV incident Au ions, only small and isolated amorphous pockets remain after annealing. The results confirm the radiation resistance of MgO, and its ability to regain the crystal lattice after more than 100,000 atoms are displaced from the small defect production region. These results are likely to contribute to understanding potential radiation effects in MgO relative to future uses in fission or fusion reactors.

Conclusion

Molecular dynamics simulations with a splined Buckingham+ZBL potential are performed to determine the directional dependence of the TDEs for Frenkel pair formation in MgO with single and multiple incident Au ions and to calculate the TDE probability distributions for the displacement of an atom by Mg and O PKAs. The simulations also investigated irradiation effects in MgO by single and multiple incident Au ions of different energies. These effects include the composition, size, and evolution of the defect clusters and the extent of the defect cascades both at the peak of the ballistic phase of interaction and after annealing. For the same total energy, irradiation effects by single incident Au ions of 5, 10, 20, and 50 keV are compared to those produced by 5 and 10 incident ions of 5, 10, and 20 keV each. Defects production, clustering, and recombination and potential ballistic melting of MgO are determined both at the peak of the ballistic phase and after annealing.

The determined TDEs corresponding to 50% displacement probability of an atom by O and Mg PKAs are 94 eV and 91 eV, respectively. These values could be used in the input of binary collision approximation codes to estimate the irradiation dose, in displacement per atom (dpa), for relevant applications. Single incident Au ions primarily produce point defects and small defect clusters, while multiple ions produce large defect clusters.

The production and clustering of defects, and the potential for ballistic melting strongly depend on the number of the incident ions, and to a lesser degree on the total energy of the ions. The number of residual defects produced by 10 5-keV Au ions is approximately an order of magnitude higher than those by 5 20-keV Au ions, with twice the total energy. With multiple incident ions, the size of the produced clusters of vacancies and interstitials are significantly larger due to the overlapping of the defect cascades produced by the individual ions. The sizes of these clusters are largest at the peak of the ballistic phase but decrease significantly during the annealing phase due to the recombinations of point defects.

Simulated SAED patterns and RDFs of the simulation results show that 10 20-keV incident Au ions cause extensive melting at the peak of the ballistic phase. However, after annealing the crystalline order is largely restored. However, small defect clusters and localized pockets of crystalline disorder remain.

The determined projected area of the defects region produced by a single 20 keV Au ion is 1.95 nm2 (1.5 nm × 1.3 nm) at the peak of the ballistic phase, .This area decreases to 0.94 nm² (0.97 nm × 0.97 nm) after annealing. With 5 20-keV Au ions, the projected area of the defects production region increases to 8.64 nm² (2.4 nm × 3.6 nm) and 5.88 nm² (2.1 nm × 2.8), at the peak of the ballistic phase and after annealing, respectively. With 10 20-keV incident Au ions, these areas increase further to 65.9 nm² (7.4 nm × 8.9 nm) and 43.9 nm² (6.1 nm × 7.2 nm), at the peak of the ballistic phase, and after annealing.

Results also show that the core of the defects production region consists mostly of immobile vacancies, surrounded by mobile interstitials. This suggests that with increased temperature, the highly mobile interstitials are likely to diffuse and recombine with the vacancies, thus reducing the residual defects in MgO. In this case, the vacancy rich regions would act as recombination centers for the diffusing interstitial atoms, reducing radiation effects. The results of the present work are timely for assessing poetical irradiation effect on MgO in next generation nuclear reactors and for the accident tolerant fuel systems in current commercial Light Water Reactors for enhanced safety and performance.

References

1. Uberuaga, BP, E Martínez, D Perez and A Voter. â??Accelerated molecular dynamics methods in a massively parallel world.â? Comp Mater Sci (2018): 147 282.
2. Yvon, P. â??Structural materials for generation iv nuclear reactors.â? Woodhead Publishing (2016).
3. Zinkle, SJ, KA Terrani, JC Gehin, and LJ Ott, et at. â??Accident tolerant fuels for LWRs: A perspective.â?  J Nucl Mater (2014): 448 374.
4. Katoh, Y, K Ozawa, C Shih, and T Nozawa, et al. â??High-dose neutron irradiation of hi-nicalon type s silicon carbide composites Part 2: Mechanical and physical properties.â? J Nucl Mater (2014): 448 448.
5. Katoh, Y, LL Snead, I Szlufarska and WJ Weber. â??Radiation effects in SiC for nuclear structural applications.â? Curr Opin Solid St M (2012): 16 143.
6. Pint, BA, KA Terrani, Y Yamamoto and LL Snead. â??Material selection for accident tolerant fuel cladding.â?  Metall Mater Trans E (2015): 2 190.
7. Powers, JJ, WJ Lee, F Venneri, and LL Snead, et al. â??Fully Ceramic Microencapsulated (FCM) Replacement Fuel for LWRs.â? Oak Ridge National Laboratory and Korea Atomic Energy Research Institute (2013).
8. Snead, L, K Terrani, J Kiggans, and B Pint, et al. â??Fully ceramic microencapsulated fuel design and irradiation testing.â? J Nucl Mater (2012).
9. Snead, LL, KA Terrani, Y Katoh, and C Silva, et al. â??Stability of SiC-matrix microencapsulated fuel constituents at relevant LWR conditions.â? J Nucl Mater (2014) 448: 389.
10. Koo, YH, JH Yang, JY Park, and KS Kim, et al. â??KAERIâ??s development of LWR Accident-Tolerant Fuel.â? Nucl Technol (2014) 186: 295.
11. Arborelius, J, K Backman, L Hallstadius, and M Limback, et al. â??Advanced doped UO2 pellets in LWR applications.â? J Nucl Sci Technol (2006) 43: 967.
12. Xie, X, R Kumar, J Sun and L Henson. â??Structure and conductivity of yttria-stabilized zirconia co-doped with Gd2O3: A combined experimental and molecular dynamics study.â? J Power Sou (2010) 195: 5660.
13. Rezaee, S, GR Rashed and M Golozar. â??Electrochemical and oxidation behavior of yttria stabilized zirconia coating on Zircaloy-4 Synthesized via Sol-Gel Process.â? Int J Corrosion (2013).
14. Deck, CP, GM Jacobsen, J Sheeder, and O Gutierrez, et al. â??Characterization of SiCâ??SiC composites for accident tolerant fuel cladding.â? J Nucl Mater (2015) 466: 667.
15. Herderick, ED, K Cooper and N Ames, â??New approach to Join SiC for accident-tolerant nuclear fuel cladding,â? Adv Mat & Pro (2012) 170 (1): 24-27.
16. Cowen, BJ and MS El-Gen. â??Point defects production and energy thresholds for displacements in crystalline and amorphous SiC.â? Comp Mater Sci (2018) 151: 73.
17. Ivekovic, A, S Novak, G Drazic, and D Blagoeva, et al. â??Current status and prospects of SiCf/SiC for fusion structural applications.â? J Eur Ceram Soc (2013) 33: 1577.
18. Yun, YH, YH Park, MY Ahn and S Cho. â??CVR-SiC coating of graphite pebbles for fusion blanket application.â? Ceram Int (2014) 40: 879.
19. Zinkle, SJ and LL Snead. â??Influence of irradiation spectrum and implanted ions on the amorphization of ceramics.â? Nucl Instrum Meth B (1996) 116: 92.
20. Sabochick, MJ and NQ Lam. â??Radiation-induced amorphization of ordered intermetallic compounds CuTi, CuTi2, and Cu4Ti3: A molecular-dynamics study.â? Phys Rev B (1991) 43: 5243.
21. Cowen, BJ and MS El-Genk. â??Point defects production and energy thresholds for displacements in crystalline and amorphous SiC.â? Comp Mater Sci (2016) 117: 164.
22. Cowen, BJ and MS El-Genk. â??Directional dependence of the threshold displacement energies in metal oxides.â? Model Simul Mater Sc (2017) 25: 085009.
23. Robinson, M, NA Marks and GR Lumpkin. â??Structural dependence of threshold displacement energies in rutile, anatase and brookite TiO2.â? Mater Chem Phys (2014) 147: 311.
24. Robinson, M, NA Marks, KR Whittle and GR Lumpkin. â??Systematic calculation of threshold displacement energies: Case study in rutile.â? Phys Rev B (2012) 85: 104105.
25. Samolyuk, GD, YN Osetsky and RE Stoller. â??Molecular dynamics modeling of atomic displacement cascades in 3Câ??SiC: Comparison of interatomic potentials.â? J Nucl Mater (2015) 465: 83.
26. Cowen, BJ and MS El-Genk. â??Estimates of point defect production in a-quartz using molecular dynamics simulations.â? Model Simul Mater Sc (2017) 25: 055001.
27. Gao, F, WJ Weber and R Devanathan. â??Nuclear Instruments and methods in physics research section B: Beam Interactions with Materials and Atoms.â? Phys Rev B (2001) 180: 176.
28. Bai, XM and BP Uberuaga. â??Multi-timescale investigation of radiation damage near TiO2 rutile grain boundaries.â? Philos Mag (2012) 92: 1469.
29. Uberuaga, B, R Smith, A Cleave, and G Henkelman, et al. â??Dynamical simulations of radiation damage and defect mobility in MgO.â? Phys Rev B (2005) 71: 104102.
30. Uberuaga, B, R Smith, A Cleave, and F Montalenti, et al. â??Structure and mobility of defects formed from collision cascades in MgO.â? Physical review letters (2004) 92: 115505.
31. Trachenko, K, MT Dove, E Artacho, and IT Todorov, et al. â??Atomistic simulations of resistance to amorphization by radiation damage.â? Phys Rev B (2006) 73: 174207.
32. Aidhy, DS, PC Millett, D Wolf, SR Phillpot, and H Huang, â??Kinetically-driven point-defect clustering in irradiated MgO by molecular dynamics simulationâ? Scripta Materialia (2009) 60: 691.
33. Plimpton, S. â??Fast parallel algorithms for short-range molecular dynamics.â? J Comput Phys (1995) 117: 1.
34. Lewis, GV and CRA Catlow. â??Defect studies of doped and undoped barium titanate using computer simulation techniques.â? J Phys C Solid State (1985) 18: 1149.
35. Polak, E and G Ribiere. â??Note sur la convergence de méthodes de directions conjuguées.â? Rev Fr Inform Rech O (1969) 3: 35.
36. Stukowski, A. â??Extracting dislocations and non-dislocation crystal defects from atomistic simulation data.â? Model Simul Mater Sc (2010) 18: 015012.
37. Coleman, SP, DE Spearot and L Capolungo. â??Virtual diffraction analysis of Ni [0 1 0] symmetric tilt grain boundaries.â? Model Simul Mater Sc (2013): 21.
38. Ayachit, U. â??The paraview guide: A parallel visualization application.â? ACM journal (2015).
39. Park,B, WJ Weber and LR Corrales. â??Molecular dynamics study of the threshold displacement energy in MgO.â? Nucl Instrum Meth B (2000) 166: 357.
40. Geisler, T, K Trachenko, S Rios, and MT Dove, et al. â??Impact of self-irradiation damage on the aqueous durability of zircon (ZrSiO4): implications for its suitability as a nuclear waste form.â? J Phys-Condens Mat (2003) 15: L597.
41. Trachenko, K, MT Dove and EKH Salje. â??Reply to comment on 'Large swelling and percolation in irradiated zircon'.â? J Phys-Condens Mat (2003) 15: L1.