Thesis - (2022) Volume 10, Issue 7
Received: 20-May-2022, Manuscript No. JAAT-22-64368;
Editor assigned: 23-May-2022, Pre QC No. JAAT-22-64368(PQ);
Reviewed: 08-Jun-2022, QC No. JAAT-22-64368;
Revised: 20-Jul-2022, Manuscript No. JAAT-22-64368(R);
Published:
29-Jul-2022
, DOI: DOI: 10.37421/ 2329-6542.2022.10.220
Citation: Chouhan, Deepanshu. "Mass-Wavelength Relation
in Curved Space-Time Fabric of a Black Hole and Transformation
of a Black Hole to a White Hole." J Astrophys Aerospace Techno 10 (2022): 220
Copyright: © 2022 Chouhan D. This is an open-access article distributed under the terms of the creative commons attribution license which permits unrestricted
use, distribution and reproduction in any medium, provided the original author and source are credited.
According to Stephen Hawking, black hole create and emit particles thereby evaporating and losing their mass slowly with time. As it loses its mass, the wavelength of the emitted particles decreases and the energy of the black hole radiation increases. The wavelength of Hawking radiation is related to the curvature of space-time continuum near the event horizon by the equation
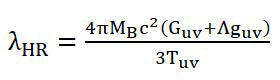
where λHR is the wavelength of the Hawking radiation. Also, by subtracting this equation from the net energy content of the black hole before emission, we can get the energy of the black hole after emission. Since black holes emit radiation that has immense pressure when it’s mass tends to zero then due to radiation pressure exerted on a body will prevent it from crossing the event horizon which is a property of white holes. In this way a black hole may behave as a white hole.
Wavelength • Emission • Radiation • Vacuum
Since black holes radiate Hawking which takes energy from the black hole itself there by evaporating it. This is a really gradual process that can take billions of trillions of years but after this much time it would inevitably be dawned by time. The process of evaporation via H.R. may take time that is much more greater than the age of the universe itself [1].
Mass-wavelength relation
In Hawking radiation the temperature of the radiation emitted by the black hole is
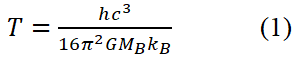
Where h, c, G, and kB are Planck’s constant, speed of light in vacuum, constant of gravitation and Boltzmann constant respectively and MB is the mass of the black hole.
Since we know that the geometry of space time is affected by the distribution of matter in the system we happen to be considering. Einstein field equation tells us how space-time curves around objects that have mass. By rewriting the EFE as:
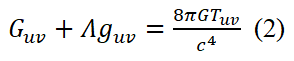
Now since in equation
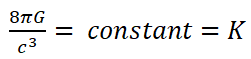
This constant it can also be seen in the equation that gives us the temperature of black hole, so by substituting K in equation [1], we get that the temperature of the radiation is proportional to the energy and momentum contained in the system.
So,
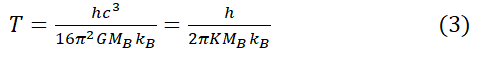
This is equal to
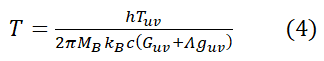
By considering the black hole and the area surrounding it to be an isolated system, we can infer that the energy of the particles in the radiation is proportional to the temperature of the radiation by some constant. Hence

where E in the energy of the radiation. Using equation (4) in equation (3) we get that the Emitted particles is proportional to the stress energy tensor and is inversely proportional to the mass of the black hole itself and the curvature it produces.
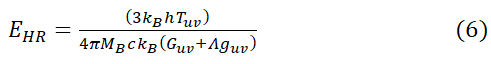
Here this equation boils down to the required equation of energy of Radiation. Note that Fun is the energy of Hawking radiation. So, the required equation.
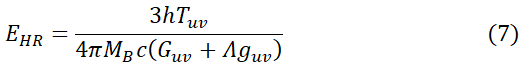
Also, by using the De-Broglie’s equation of energy frequency relation which states that the frequency of the electromagnetic radiation depends upon the energy of the same.

where E, h and F are the energy, Planck’s constant and frequency of radiation respectively.
Furthermore, frequency of any electromagnetic radiation is equals to speed of light in vacuum divided by wavelength of radiation [2].
So,

Here lambda is the wavelength of radiation.
Since, we know that both the energy equations are equal because of the fact that radiation in equation (6) is same as that of (8) hence,
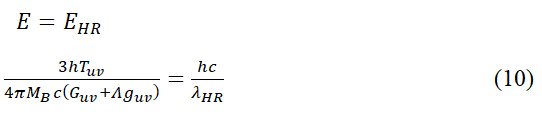
Solving for the Hawking Radiation wavelength gives us

This is the mass-equivalence wavelength equation. From this equation we get the result that the wavelength of the Hawking radiation emitted by a small black bole is smaller than the wavelength emitted by a supermassive one.
From this equation we can also conclude that the evaporation of a black hole gets faster and faster as it loses its mass. Smaller black holes or stellar mass black holes will evaporate faster as compared to a super-massive black holes [4].
Now, since we know that black holes emit radiation in a very wide range of electromagnetic spectrum. We can solve the previous, equation for the mass of a black hole that would emit radiation in the visible spectrum of humans.
By using equation (10) and rearranging the constants we get that:

Note that except λHR and MB, all other quantities are constant so, by solving this quantities we get:

where U is the change in wavelength per unit change in mass with a value of 7.817 х 1028 m/kg
Furthermore, by the fact that the visible range of electromagnetic spectrum lies from ~ 400 nm to 700 nm, we can deduce the mass of a Black hole that could give off visible light.
From equation 2:

Plugging in the values for lambda to be 400 nm and 700 nm and putting value of U we get the any black hole having mass in the Range of ~ 5.123 х 1018 Kg to 8.966 х 1018 kg and a Schwarzschild radius of about 7.608 х 10-9 to 13.316 х 10-9 will emit Hawking radiation in the visible range of the electromagnetic series [5].
Here, one should note that the radiation is not coming from inside of the black hole but rather from just above the event horizon.
Also by manipulating the above equation we can get change in wavelength per unit change in mass, let us assume that the unit change in wavelength is dλHR and unit change in mass to be a dMB then from equation (12).


So, the change in wavelength of Hawking radiation per unit change in black hole’s mass is a constant.
where the slop of the line AB is U (wavelength decrement factor). Putting this in the Schwarzschild radius equation:-

Recall,
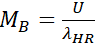
Hence,

Also,
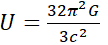
This implies that

Let s assume 3/(16 π2 )= ξ =1.899 х 10-2 which is the radius decrement factor by wavelength.
Again by using equation (20) we can calculate the area and volume of a black hole in 3-spatial dimensions. Here one must note that it can’t calculate the volume precisely as inside the black hole there can be many entangled dimensions which we don’t yet understand [6].
Since,.
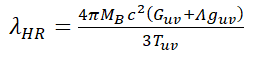
By dividing and Multiplying by Rs2:
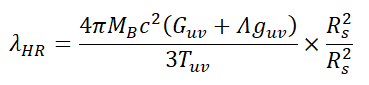
Since 4πR2= surface area of sphere
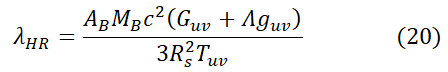
Where AB is the area of the event horizon. Similarly by dividing and multiplying by Rs3:
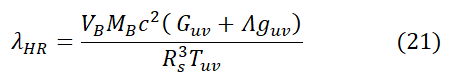
Where VB is the volume of black hole in spatial dimensions that we live in.
Since black holes also emit radiation hence they can also be luminous although their luminosity can be billions of trillions of degree lower than a main sequence star. Luminosity of black hole is inversely proportional to the square of mass of the same times some constant [7].
This can be figured out as:
From equation (9), putting the value of constant we get:

Divide and multiply by MB and solving for AB:

Putting expressions from equation (3) and (10) in equation of luminosity:

Here L denotes luminosity ,σ is Stefan’s constant and T is temperature. Substitute in all the constant terms and solve for L,
Hence the required expressions is:

Furthermore λHR/MB=U, this implies:
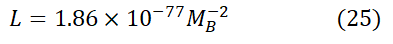
Which is a very small number that signifies to what extent black hole can absorb matter and radiation.
As the black hole loses mass and shrinks it’s temperature increases to such high degrees that are unimaginable, at the same time the wavelength of HR also decreases increasing the overall energy of radiation. After a long time when the black hole is in its final stage ( M tends to 0) it starts emitting more energy than what it gasps in and the pressure exerted by the radiation becomes high enough to prevent anything from falling into the event horizon. Now this definition fits perfect with what white holes are.
This may mean that black holes and white holes are not two different objects but rather the same object seen after a long period of time. But as the mass tends towards zero energy emitted tends to infinity which can create the environment that was at the time of big bang and this may help us to know how our universe came into being. Maybe it was an evaporating black hole from a previous universe or maybe something more bizarre.
Net energy content of a black hole
A black hole can swallow anything that is within its innermost stable orbit or anything that gets too close to the event horizon. By doing so it can grow in size and can become more massive which also gives rise to many paradoxes like the famous information paradox in which all the information of an in falling object becomes inaccessible to an outside observer. Is the information erased from our universe, if we go with conservation of energy then the total energy of the universe must be same, and all the information is energy in general. This could imply that black hole may be converting all the energy that it absorbs into some other form mainly radiation.
Now, the net energy of a black hole will depend on it’s energy by mass and spin. If we consider some matter to be falling inside the event horizon then it would also add to the total energy [8].
Also one must recall that the emission of Hawking radiation decreases its mass so we would have to subtract it from the equation:
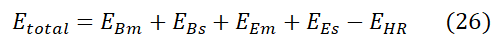
Where EBm, EBs, EEm, EEs, EHR are energy by mass of BH, energy by spin of black hole, energy by mass of external matter and energy of Hawking radiation. By using this equation we can deduce the total energy of a black hole.
A black hole can emit radiation and evaporate but this takes a long period of times. As it evaporates it’s energy tends towards infinity creating secondary big bang. After long time black hole becomes white hole and prevents anything from falling into the event horizon. This may suggest the reason why we haven’t seen any white hole yet because they aren’t formed yet and till they form we might not exist.
This manuscript is not published or under consideration in any other journal. This research is original and done as an extension of previous work done by Stephen Hawking on the subject of radiation emitted by a black hole.
Astrophysics & Aerospace Technology received 114 citations as per Google Scholar report