Research Article - (2024) Volume 13, Issue 3
Received: 05-Mar-2024, Manuscript No. jacm-24-128809;
Editor assigned: 07-Mar-2024, Pre QC No. P-128809;
Reviewed: 18-May-2024, QC No. Q-128809;
Revised: 23-May-2024, Manuscript No. R-128809;
Published:
30-May-2024
, DOI: 10.37421/2168-9679.2024.13.560
Citation: Muthu, Poosan and A. Samatha. “Mathematical Modelling of an Oscillatory Flow of a Casson Fluid in an Elastic Tube with Suction/Injection.” J Appl Computat Math 13 (2024): 560.
Copyright: © 2024 Muthu P, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In the current mathematical model, examined the oscillatory flow of a Casson fluid in a thin walled elastic tube with a varying cross-section by assuming suction or injection at the tube wall and also permeability. The problem is developed that the elastic tube connects against longitudinal displacements. The perturbation approach is used to linearize the nonlinear governing equations to solve the flow characteristics. The differential equation for the pressure is solved numerically along with the corresponding initial conditions using Gill’s fourth order. The effects of Womersley parameter, velocity at the wall(suction/injection), elasticity parameter and Casson parameter on the modulus of wall shear stress and mean pressure drop are discussed through the graphs. Further noted that in a case of a locally constricted tube, the diverging part’s modulus of wall shear stress drops while the convergent part’s rises as Casson parameter, Womersley parameter increases.
Casson fluid • Suction/Injection • Elasticity • Oscillatory flow • Perturbation scheme • Gill’s method of fourth order
76D05; 76Z05; 35Q30
The non-Newtonian fluids are spread and serve as proof of ongoing research, because of its passionate contribution to the fields of mathematics, physiology, engineering, and industry; because of their intricacy these fluids are complicated in nature. The study of blood flow aims to determine the pressure and flow through the vessels, both of which are important to human health. Recognizing the features of blood flow via the arteries is also beneficial. It is necessary to comprehend blood flow dynamics in order to diagnose and treat a variety of cardiovascular and cerebrovascular diseases.
The oscillatory flow of a Casson fluid in an elastic tube with varying cross sections has attracted a lot of attention in the study of fluid mechanics. Blair, GWS studied the blood flows through arteries with a bigger diameter and higher shear rates, exhibits the characteristics of a Newtonian fluid; yet, when blood flows through arteries with a smaller diameter and lower shear rates, behaves like a non-Newtonian fluid [1]. The Casson fluid model is a non-Newtonian fluid with yield stress that is mostly used to simulate low shear rate blood flow in small arteries, also highlighted that the bigger suspended particles in blood, travel closer to the plasma walls, when it passes through small tubes and also developed an equation for the flow of blood, plasma, and serum via glass capillaries. Rao RA revealed many interesting results from the graphs of the excess pressure with different geometries and physical parameters such as Womersley, elastic for an oscillatory flow in an elastic tube [2]. Nakamura M and Sawada T explored on the laminar pulsating flow of slurries, also referred that as a Bingham plastic fluid [3,4]. The equations of bi-viscosity model were used in the computations. Additionally studied numerically the non-Newtonian fluid flow via axisymmetric stenosis.
Vajravelu, K, et al. developed a mathematical representation for an elastic tube filled with a steady, laminar, incompressible Herschel-Bulkley fluid [5]. The flow rate was examined by the researchers over a range of yield stress, elastic parameter, and shear thickening fluid values. Sreenadh S, et al. was investigated the unsteady Jeffrey fluid in an elastic pipe with stenosis [6]. The fluid flow velocity and excess pressure were the authors main concerns. The results for the excess pressure with various Jeffrey and elastic parameter values were examined.
Selvi PD, et al. examined a Casson fluid of oscillatory motion in an elastic tube with varying cross-section [7]. Also analysed the pressure distribution for various pressure-radius relations was done for different kind of geometries. Diagrams were used to illustrate a number of interesting findings on the impacts of Womersley parameter, elasticity, and Casson factors on the excess pressure. Through the results identified that pressure oscillates more in the case of a locally constricted tube than it does in the other geometries.
Chandra P and Prasad JSVRK [8] investigated a pulsatile flow in a circular tube with suction/injection of varying cross-section. The main study of the authors was varying of Womersley parameter and Reynolds number with the suction/injection velocity, observed that the effect on wall shear stress modulus, pressure drop.
Blood flow in an elastic tube is oscillatory in nature. The elastic tube along its length and cross-sectional area can be impacted by the oscillations of a Casson fluid. By applying suction/injection for the specific values as well as Casson parameter values along the tube can change the flow characteristics. The effects of suction/injection for an oscillating flow of a Casson fluid in an elastic tube of different cross-sections is important in multiple fields such as biomedical engineering, cardiovascular research and fluid dynamics.
We have analysed the oscillatory flow of Casson fluid in arteries with a permeable wall and varying cross-section is explained in the current mathematical model. The permeable wall is determined by defining the normal velocity at the wall. In this analysis, we assume that the blood is a non- Newtonian (Cassson) fluid in narrow arteries. The wall permeability, specifies the transport of small molecules through the walls of the blood vessels. Further, the effect of elastic parameter, Casson parameter, Womersley parameter and wall velocity (due to suction/injection) on both the modulus of shear stress and mean pressure drop at the tube wall are demonstrated graphically in this analysis.
Problem statement
We have analysed the Oscillating motion of an incompressible Casson fluid in an elastic tube with thin walls and a circular cross-section, where the walls are suctioned or injected. It is assumed that the elastic tube is connected against longitudinal displacements as shown in Figure 1. The tube radius changes gradually along the axial direction. We considered cylindrical polar coordinates (r, z, Θ) to describe the elastic tube. The constitutive equation for Casson fluid by Nakamura M and Sawada T [4] is expressed in Eq. (1). If r=0 is the axis of symmetry of the tube, then the tube radius r=a (z) is expressed in Eq. (2)

Here τij, eij are the (i, j)th components of stress tensor, deformation rate with itself. πc is the critical value of this product, μb is the plastic dynamic viscosity of the non-Newtonian fluid. Py is the yield stress of the fluid, β is the Casson parameter. a0 denotes radius of the tube at z=0 and L is the characteristic length of the tube. Note that ϵ=0 cases represent the fluid in the tube of uniform radius (Figure 1).
Figure 1. Geometry of the two dimensional elastic tube of circular cross-section.
The basic equations of continuity and motion governing an axisymmetric fluid flow are:

Where w and u are the axial and radial components of the fluid’s velocity is the kinematic viscosity coefficient, ρ0 is the constant fluid density, p is the pressure and t indicates time variable.
We assumed the elastic tube to be connected against the longitudinal displacement. Consequently, the shell equation of the wall for longitudinal displacement is zero, while the equation governing radial displacement ξ which takes place due to the narrowing(constriction) of the tube is given as [4]:

Where h and ρ indicates thickness and density of material of the tube
respectively and 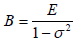
E corresponds to Young’s modulus and σ stands for the Poisson’s ratio [4].
Normal component of the fluid velocity at the wall of the tube i sexpressed as [8]:

Here ūw = uw ei ω t is the oscillatory fluid velocity due to which suction/
injection occurs at the permeable wall, ω represents the frequency of the
oscillation and  is the wall velocity due to the flexibility of the tube wall [8].
is the wall velocity due to the flexibility of the tube wall [8].
Tangential velocity at the wall is zero (no-slip condition) implies
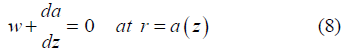
The axisymmetry of the flow is

The flow rate Q(z) is prescribed at the entrance cross section of the tube as:

Where Q0 is constant.
Analysis
We introduce the following dimensionless quantities for the Eqs. (2-10).

Thus, the Eqs. (2-10) reduced into the dimensionless form after removing stars and expressed as below:
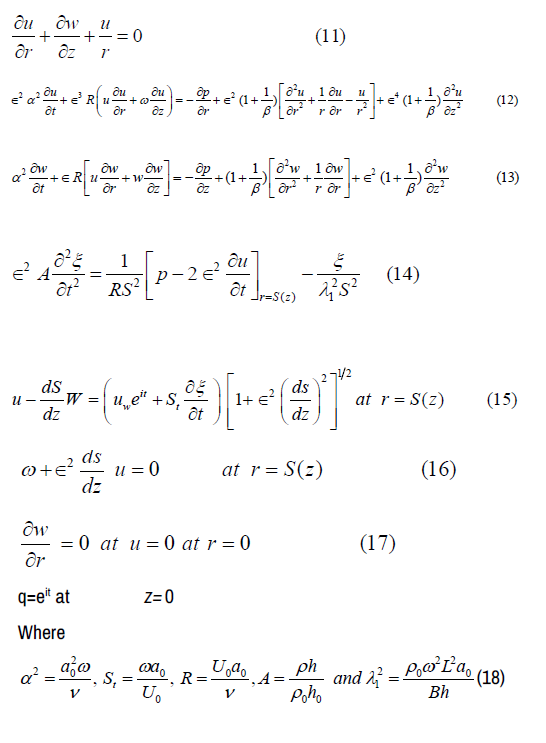
Here, α is the Womersley parameter, St is the Strouhal number and R is the Reynolds number,
A and λ21 are the dimensionless numbers involved in wall properties. Parameter λ1 indicates the elasticity of the wall and λ1=0 performs the case of rigid walls.
Note that uw=0 simplifies Rao’s analysis [2], in which the author considered only zeroth order in ϵ.
Method of solution
Analyze the solution for flow variables based on the assumption of steady oscillations in the following form:
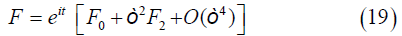
Where F (r, z, t) is used for any of the flow variables u, w, p and ξ. Substituting the expression Eq. (19) in Eqs. (11- 18) and considering the coefficients of the like powers of ϵ0 and ϵ2 by ignoring the terms of order greater than two, then the governing equations of zeroth and second order approximations together with their respective boundary conditions are listed below.
Zeroth order in ϵ:


Solving the Eqs. (20-22) along with boundary conditions Eqs. (23-26), we get the solution for w0 and u0 as:
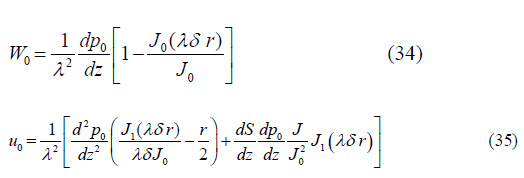
Where Jm(λδ r) denotes the Bessel function of order m and Jm ≡ Jm(λδ S). The Eq. (34) gives the zeroth order flux q0 as,

Using the expression Eq. (35) for u0 and integrating Eq. (29), We get the p2 in the following form where f (z) is to be found, by using the condition p2=0 at z=0.
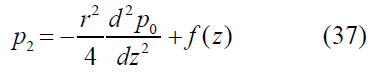
By solving Eqs. (27,28) using the Eqs. (34-37) by substituting the corresponding boundary conditions then we obtain w2 and u2 as:

Using the Eq. (38) for w2, we obtain the expression for q2 as,

Substituting the expressions for p2, u0 and ξ0 in Eq. (30), we get ξ2 as:
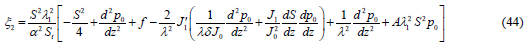
Now, to obtain the equation governing pressure, we use the conditions (23) and (24) the expressions for u0 and ξ0, we get,
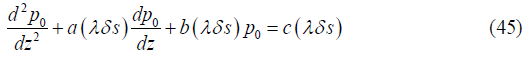
The initial conditions for p0 are prescribed as:

The initial conditions for p0 are prescribed as:
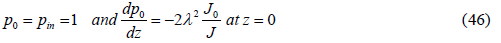
(31) Along with the expressions 39-44 for u2 and ξ2 give the differential equation determining f (z) as

The corresponding initial conditions are obtained from Eqs. (33-43) as:
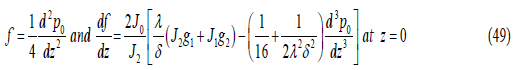
The differential Eq. (45) for p0 (z) and the Eq. (47) for f (z) solved numerically along with the corresponding initial conditions using Gill’s method. Then the modulus of pmean is

The mean pressure drop is
Δp = pin − pmean
Wall Shear Stress: The non-dimensional wall shear stress Tw is [8],

Now the modulus of wall shear stress is
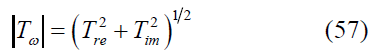
Where Tre and Tim represent the real and imaginary parts of Tw respectively and can be obtained using the Eqs. (52-56).
The equations for the modulus of wall shear stress | Tw | from Eq. (57) and the mean pressure drop Δp from Eq. (51) are numerically evaluated with the corresponding initial conditions using
Gill’s method of order 4 and plotted in the respectively (Figures 2-17).
Figure 2. Modulus of wall shear stress vs. z for a convergent tube with α = 4, λ1 = 0.
Figure 3. Modulus of wall shear stress vs. z for a convergent tube with α = 4, λ1 = 0.25.
Figure 4. Modulus of wall shear stress vs. z for a convergent tube with α = 6, λ1 = 0.
Figure 5. Modulus of wall shear stress vs. z for a convergent tube with α = 6, λ1= 0.25.
Figure 6. Modulus of wall shear stress vs. z for a divergent tube with α = 4, λ1 = 0.
Figure 7. Modulus of wall shear stress vs. z for a divergent tube with α = 4, λ1 = 0.25.
Figure 8. Modulus of wall shear stress vs. z for a divergent tube with α = 6, λ1 = 0.
Figure 9. Modulus of wall shear stress vs. z for a divergent tube with α = 6, λ1 = 0.25.
Figure 10. Modulus of wall shear stress vs. z for a locally constricted tube with α = 4, λ1 = 0.
Figure 11. Modulus of wall shear stress vs. z for a locally constricted tube with α = 4, λ1 = 0.25.
Figure 12. Modulus of wall shear stress vs. z for a locally constricted tube with α = 6, λ1 = 0.
Figure 13. Modulus of wall shear stress vs. z for a locally constricted tube with α = 6, λ1 = 0.25.
The results are obtained by taking ϵ=0.1, A=0.055, α=4, 6, β=0.2, 0.3, 0.4, 0.5 [7] and uw=−0.4, 0.0, 0.4 and [8] for the tube geometries below
(i) Convergent tube: S(z)=e−0.1z
(ii) Divergent tube: S(z)=e0.1z
(iii) Locally constricted tube: 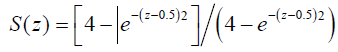 It is observed that the
expressions for | Tw | and Δp depends on the dimensionless parameters
such as α2 (Womersley parameter), λ1 (elasticity parameter), uw (velocity
at the wall), β (Casson parameter).
It is observed that the
expressions for | Tw | and Δp depends on the dimensionless parameters
such as α2 (Womersley parameter), λ1 (elasticity parameter), uw (velocity
at the wall), β (Casson parameter).
Magnitude of wall shear stress
Convergent tube: The result of magnitude of wall shear stress | Tw | are plotted in the Figures 2-5 for a convergent tube with the Womersley parameter values 4 and 6, Casson parameter values 0.2, 0.3, 0.4 and 0.5 respectively. Here the graph of magnitude of wall shear stress is plotted with respect to z.
In the case of rigid tube wall (λ1=0.0), the magnitude of wall shear stress is expands with the increasing of Casson parameter, Womersley parameter values. The magnitude of wall shear stress is higher when compared to the case of elastic tube wall (λ1=0.25).
Suction diminishes as reducing the values of Womersley parameter and Casson parameter values for elastic tube wall and it is shown in the Figures 3-5,
Injection expands widely and it is shown in the Figures 2-5 when compared with the case of suction (uw=0.4).
As α, β increases the value of magnitude of wall shear stress rises in both suction and injection cases.
Divergent tube: For a divergent tube, the wall shear stress modulus is plotted in the Figures 6-9 with different values of Womersley parameter, Casson parameter.
Suction drop down as in both the cases rigid and elastic tube wall cases comparing to injection case (uw=−0.4). As increasing of Casson parameter the modulus of wall shear stress increases slightly as in both rigid, elastic tubes.
In general, higher Casson parameter β indicates, the decreasing yield stress and also decreases the velocity field.
Locally constricted tube: The profile of modulus of wall shear stress | Tw | is plotted in the Figures 10-13 for a locally constricted tube with different values of Womersley parameter values 4 and 6, Casson parameter values 0.2, 0.3, 0.4 and 0.5 respectively.
In locally constricted tubes, the wall shear stress modulus increases gradually with Casson parameter values from 0.2 - 0.5 in the convergent part and diminishes in the divergent part for α=4, 6. This phenomenon is observed both in the rigid and elastic tubes.
However in the elastic tubes suction suddenly downfall occurs at the same value as in the case of α=4 compared to α=6.
Injection rises up and reduces the flow at the elastic tube wall in both the cases of Womersley parameter values.
Mean pressure drop
The profile of mean pressure drop Δp is plotted in the Figures 14-17 for a locally constricted tube.
Now the mean pressure drop is plotted vs. z (in axial direction).
Increasing Casson parameter, diminishes the pressure drop Δp for a locally constricted tube. The behaviour of suction or injection on mean pressure drop is generally the same, no specific identity whether it is suction or injection at the tube wall. This pattern depends on the flow conditions and the characteristics of the suction or injection process. In case of suction (uw=0.4) the mean pressure drop is smaller than comparing to the case of injection (uw=−0.4).
Mean pressure drop higher in all the cases mainly for β=0.2 comparing with the other Casson parameter values. Mean pressure drop values are decreases continuously with all the Casson parameter values enhances at each cross section as it moves from x=0.0 − 1.0, in both rigid and elastic tube walls.
There is no such remarkable difference on mean pressure drop for the various tube geometries and similar observation found in convergent, divergent tubes. Moreover as the Womersley parameter α increases the mean pressure drop increases and it decreases when Casson parameter rises.
Similar behaviour of mean pressure drop Δp is observed for all the other tube geometries [9-23].
In the present study, the oscillatory of a Casson fluid in an elastic tube with suction/injection and permeability at the wall with varying cross-section is investigated. We examined the effect of Casson parameter, suction/injection velocity on wall shear stress modulus and mean pressure drop of an elastic tube wall with varying cross-sections under oscillating flow conditions. This study provides salient insights into the impacts of suction/injection, Casson parameter values on flow characteristics and signify the role of tube elasticity in mediating these effects.
By the above analysis, it has been revealed that the rise or fall in the wall shear stress modulus is not only impact by the parameters α2, λ1 and β but also by the geometry of the tube we are examining. Also note that in the suction/injection case, the mean pressure drop for both rigid and elastic wall pipes rises as the Womersley parameter increases and downfall occurs as the Casson parameter increases.
None.
None.
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report