Research - (2020) Volume 9, Issue 4
Received: 23-May-2020
Published:
02-Jun-2020
, DOI: 10.37421/2168-9679.2020.9.448
Copyright: © 2020 Mohamed Moktar Chaffar. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In the present paper we define an oriented Star with 
α coefficient α 1 and we further develop the procedure for finding eigenvalues and eigenvectors for an (5 × 5) Starmatrix directly or (5 × 5) Star-matrix indirectly. we give an overview of the methods to compute matrix-multiplication of a Star α (generally square 5 × 5) with particular emphasis on the oriented matrix.
Matrix orientation • Coefficient star-matrix
In this article, we propose a matrix representation of an oriented star with α coefficient α [1] and define two directions of orientation. It is therefore possible to orient a star with α coefficient α in two different ways, directly and indirectly (Figure 1).
Figure 1.
A star with α coefficient is composed of five numbers outside a, b, c, d, e and five numbers inside T1, T2, T3, T4, T5, These last five numbers are written in the form of 5-tuple (T1, T2, T3, T4, T5) (Figure 2).
Figure 2a.
Figure 2b.
The scalars α are called the star coefficient if α is a solution of equation α = T1 (α) + T2(α) + T3(α) + T4(α) + T5(α) (Noted by α), a vector (T1, T2, T3, T4, T5) is called a solution vector of this Star-System with coefficient α in five unknowns.
The present paper is organized as follows: In Section 2, we present some preliminary results and notations that will be useful in the sequel. In Section 3, we will use the convention here that the star α has a positive or a negative (picture 1) orientation besides orientation of a star α. Another way to think of a positive orientation is that as we traverse the path following the positive orientation the star α must always be on the left (that is, one may also speak of orientation of a (5 × 5) matrix, polynomial of degree 5, etc.). We present some examples of Star-matrix directly or indirectly.
In this section, we introduce some notations and star-system with coefficient α defined.
A star-system with coefficient α
Definition 1: Let a, b, c, d, and e and α be real numbers, and let T1, T2, T3, T4, T5 be unknowns (also called variables or indeterminates). Then a system of the form
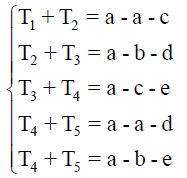
is called a star-system with coefficient α in five unknowns. We have also noted [a, b, c, d, e; α] = α. The scalars a, b, c, d, e is called the coefficients of the unknowns, and α is called the constant “Chaff” of the star-system in five unknowns.
A vector (T1, T2, T3, T4, T5) in R5 is called a star-solution vector of this star-system
If and only if [a, b, c, d, e; α] = α.
The solution of a Star-system is the set of values for T1, T2, T3, T4 and T5 that satisfies five equations simultaneously.
A star-element
A star-element is a term of the five-tuple (T1, T2, T3, T4, T5) solution of a star-system [a, b, c, d, e; α] = α, where (T1, T2, T3, T4, T5) ∈ R5.
Star-Coefficient or Constant “Chaff”
The star-Coefficient or Constant”Chaff” is also noted by α? and is a solution of equation α= T1(α )+T2 (α )+T3 (α )+T4 (α )+T5 (α ), where (T1, T2, T3, T4, T5) is solution of a star-system [a, b, c, d, e; α] = α.
Star-matrix
The star-system with coefficient α can be written in matrix form
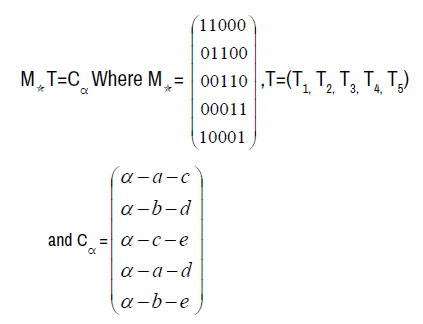
M or MStaris called the star-Matrix of the star-system with coefficient α ([a, b, c, d, e; α] = α).
M a matrix is said to be of dimension 5 × 5. A value called the determinant of M that we denote by |MStaris| or |M|, corresponds to square matrix M. Consequently, the determinant of M is |M| = 2.
Set-star
The set-star is constructed from the solution set of linear star-system with coefficient α ([a, b, c, d, e; α] = α). The Set-star will be noted by S
Star-System equivalent
Equivalent Star-Systems are those systems having exactly same solution, i.e. two star-systems are equivalent if solution of on star system is the solution of other, and vice-versa.
Parameterized curves
A parameterized differentiable curve is simply a specific subset of R5 with which certain aspects of differential calculus can be applied.
Definition 2: A parameterized differentiable curve is a differentiable map α: I → R5 of an open interval I = (a, b) of the real line R in to R5
Regular curves
A parameterized differentiable curve α: I → R5, We call any point that satisfies α 0 (t) = 0 a singular point and we will restrict our study to curves without singular points.
Definition 3: A parametrized differentiable curve is a differentiable α: I → R5 is said to be regular if α'(t)≠0 for all t ∈ I
Parametric arclength
Generalized, a parametric arclength starts with a parametric curve in R5. This is given by some parametric equations T1(t), T2(t), T3(t), T4(t), T5(t), where the parameter t ranges over some given interval. The following formula computes the length of the arc between two points a, b.
Lemma 1: Consider a parametric curve T1(t),T2(t),T3(t),T4(t),T5(t), where t ∈ (a, b). The length of the arc traced by the curve as t ranges overt (a, b) is
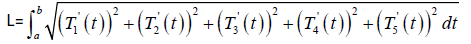
Thereafter I start with several examples with detailed solutions are presented.
Orientation of a Star
In this section, We choose two directions of travel on this Star with coefficient α can be classified as negatively oriented (clockwise), positively oriented ( counterclockwise).
Where + is a star oriented contraclockwise (positively oriented) (Figure 3):
Figure 3a.
Figure 3b.
In the first case, one obtains a new matrix noted 
called the star matrix directly
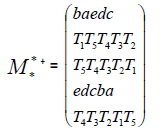
We note - is a star oriented clockwise (negatively oriented) (Figure 4):
Figure 4.
In the second case, one obtains a new matrix noted 
- called the star matrix indirectly
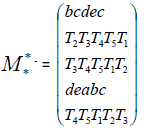
Image of a five prime numbers.
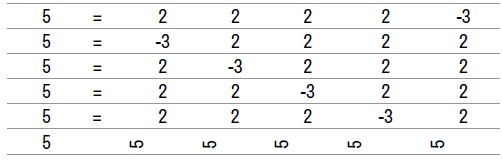
Example 1: We consider the Star-System with coefficient 
[3,7,11,13,17; α] = α of Linear Equations, we can easily solve this using Star- Matrix 
(Figure 5).
Figure 5.
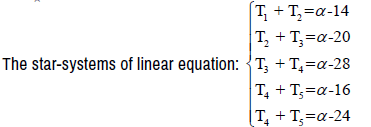
The solution of the Star-system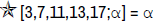 
is therefore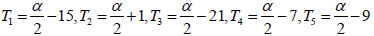 
So the overall solution is the star-set: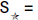 
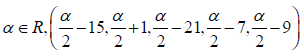
in a particular case if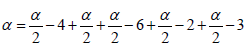 
Then
• The Star-coefficient: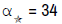
• The star-element is (2,18,−4,10,8) (Figure 6)
Figure 6.
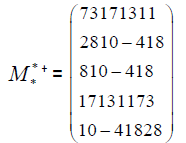
and the star matrix indirectly
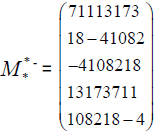
The determinant of a matrix 
is denoted det
, after numerous calculations det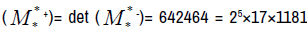 
1181 is a prime number because it has only two distinct divisors: 1 and itself (1181).
The characteristic polynomial of a matrix 
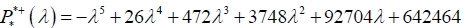
The characteristic polynomial of a matrix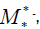 
noted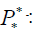 
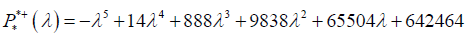
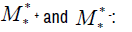
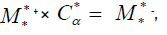
Where
called the matrix multiplication or chaffar-matrix. These results verified:
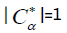
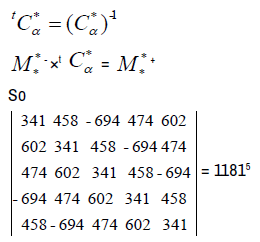
A Surprise Result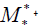 
where one of the eigenvalues is repeated noted
Now we look at matrix 
where one of the eigenvalues is repeated noted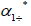 
We shall see that this.
Eigenvalues: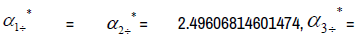 
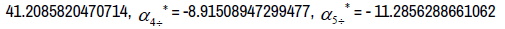
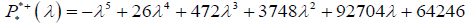
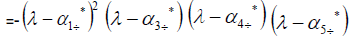
Investigate carefully the eigenvectors associated with the repeated eigenvalue
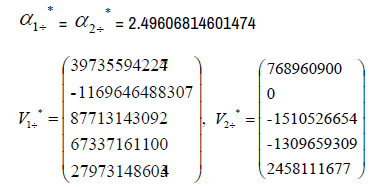
The eigenvectors associated with the eigenvalue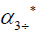 
=41.2085820470714
The eigenvectors associated with the eigenvalue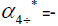 
8.91508947299477
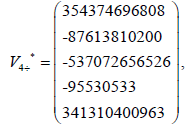
The eigenvectors associated with the eigenvalue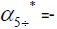 
8.91508947299477
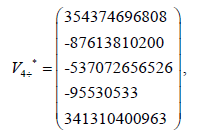
The eigenvectors associated with the eigenvalue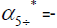 
11.2856288661062
The Eigenvalues of matrix 
α2- =0.12957478575019, α3-=41.8947762503062, α4=−14.0769629109033,
The eigenvectors associated with the repeated eigenvalue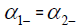 
=0.12957478575019
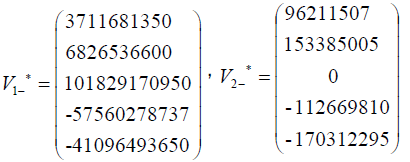
The eigenvectors associated with the eigenvalue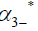 
=41.8947762503062
The eigenvectors associated with the eigenvalue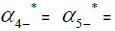 
−14.0769629109033
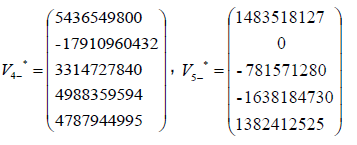
The conclusion is that since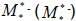 
is 5×5 and we can obtain five linearly
Independent eigenvectors then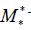 
be diagonalized.
On the other hand
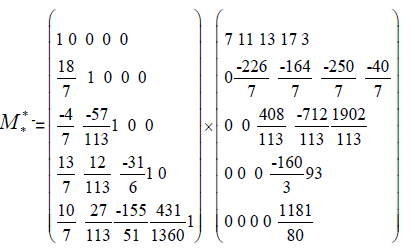
Matrix multiplication and Star-function
As we will see in the next subsection, matrix multiplication exactly corresponds to the composition of the corresponding linear transformations.
Example 2. Let α ∈R , for all t ∈R the star-system [t,2t,3t,4t,5t;α]= α has a unique solution
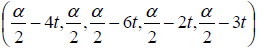
So the overall solution is the Star-set:
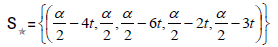
If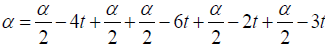 
Then
• The Star-coefficient: α* =10t
• The star-function: (t,5t,−t,3t,2t) (Picture 7)
In the special case t=3
• The Constant”Chaff”: α = 30
• The Star-set: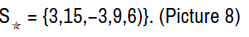 
The star matrix directly
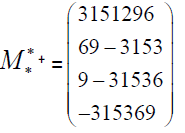
The star matrix indirectly
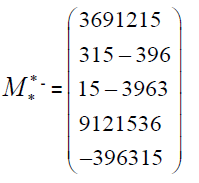
After numerous calculations det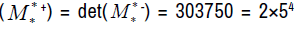 
×243, 243 is a prime number.
The characteristic polynomial of a matrix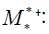 
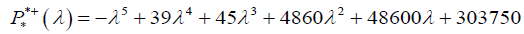
The characteristic polynomial of a matrix 
The following product was obtained from the two matices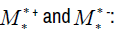 
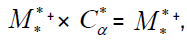
we get the following matrix:Called Chaffar-matrix
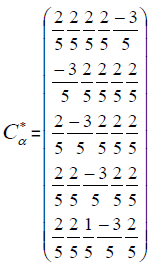
It should be hard to believe that our complicated formula for matrix multiplication actually means something intuitive such as chaining two transformations together.
Let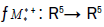 
and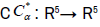 
be linear transformations, and let 
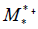and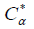
be their standard matrices, respectively, so
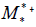is is an 5×5 matrix and 
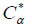is an 5×5 matrix.
Then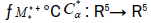 
is a linear transformation, and its standard matrix is the product 
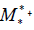that is to say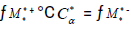
we have
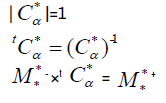
So
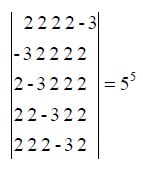
A Surprise Result
Eigenvalues of matrix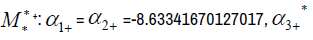 
= 35.5216112793007,
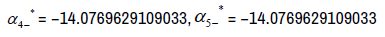
The eigenvectors associated with the repeated eigenvalue 
=-8.63341670127017
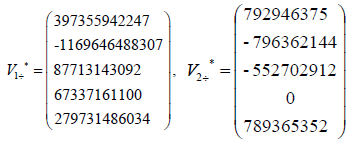
The eigenvectors associated with the eigenvalue 
35.5216112793007
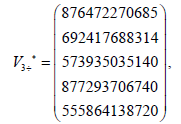
The eigenvectors associated with the eigenvalue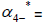 
−14.0769629109033
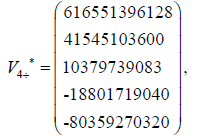
The eigenvectors associated with the eigenvalue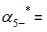 
−14.0769629109033
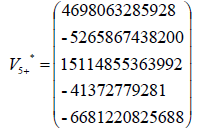
is 5×5 and we can obtain five linearly independent eigenvectors then 
be diagonal-Eigenvalues of matrix 
= 34.7324078557174,
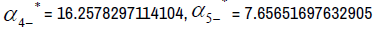
The eigenvectors associated with the repeated eigenvalue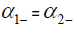 
= −6.82337727172845
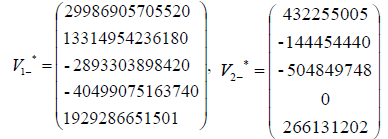
The eigenvectors associated with the eigenvalue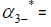 
34.7324078557174
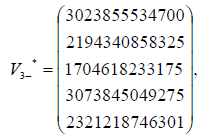
The eigenvectors associated with the eigenvalue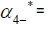 
16.2578297114104
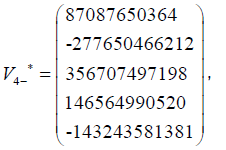
The eigenvectors associated with the eigenvalue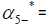 
7.65651697632905
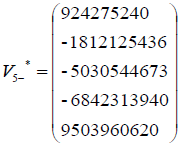
Similarly is that since 
is 5×5 and we can obtain five linearly independent eigenvectors then 
be diagonalized.
More generally,
For all t ∈ R − {0} the star-system [t,2t,3t,4t,5t;10t] = 10t has a unique solution (t,5t,−t,3t,2t), the Star-coefficient α = 10t and the star-function: t 7→ (t,5t,−t,3t,2t) (Figure 7)
Figure 7.
The star matrix directly
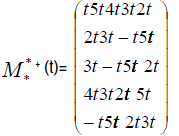
The characteristic polynomial of a matrix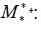 
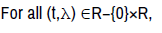
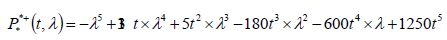
We get the star matrix indirectly
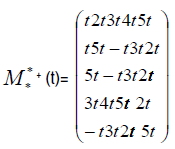
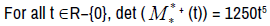
The characteristic polynomial of a matrix 
For all (t,λ) ∈R−{0}×R,
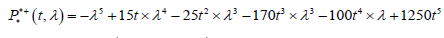
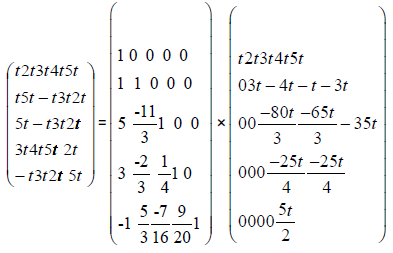
The following product was obtained from the two matices 
and
Chaffar-Matrix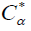 
is a matrix independent of t
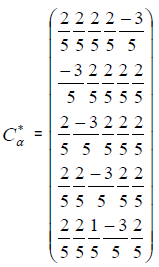
it should be hard to believe that our complicated formula for matrix multiplication actually means something intuitive such as chaining two transformations together.
The following results are obtained:
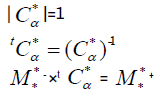
The relationship between two matrices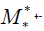 
and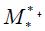 
is a convenient method of visualizing relationships quickly and definitively. One way of looking at it is that the result of matrix multiplication is important in research afterwards.
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report
