Research Article - (2021) Volume 0, Issue 0
Received: 09-Jul-2021
Published:
30-Jul-2021
, DOI: 10.37421/2090-0902.2021.s2.346
Citation: Garba, Abor Isa , Magami MS, and EJIMA O. "On the
Identity-Power Graphs of Finite Groups." J Phys Math 12:S2(2021):346.
Copyright: © 2021 Garba AI, et al. This is an open-access article distributed
under the terms of the Creative Commons Attribution License, which permits
unrestricted use, distribution, and reproduction in any medium, provided the
original author and source are credited.
Let G be a finite group, the associated identity-power graph Γ (G) is a graph whose vertices V (Γ(G)) are precisely the elements of G and two distinct vertices x,y create the oriented edge (x, y) if and only if xy=e or yx=e (where e is the identity of the group G) and either x=yn or y=xn for some n € N. We investigate some algebraic properties and combinatorial structures of the identity-power graph Γ (G) and show that the graph Γ(G) of a finite group G, is never complete. We also show that if every element x in a finite group G has a unique inverse y € G, and then the identity-power graph of G is acyclic. Furthermore, we show that the size of the identity-power graph Γ (M) of a permutation group M is given by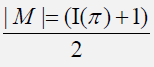
. Where π € M and I (π) is the set of involutions in M.
Entity power graphs • Finite groups • Identity graphs • Power graphs • Graph of finite groups
Let G be a finite group, the identity graph of G is an undirected simple graph whose vertex set is G and two distinct vertices x and y are adjacent if and only if xy=e or yx=e, where e is the identity of G. Similarly, the power graph of G is a simple undirected graph whose vertex set is G and two distinct vertices x and y are adjacent if and only if xn=y or yn=x for some n € N. The notions of the identity graph and the directed power graph lies in the works of respectively [1, 2]. Kandasamy and Smarandache studied the identity graph of algebraic structures that have identity; for instance, in their work, the considered the semi groups, loops, commutative groupies and commutative ring [1]. They noted that if these algebraic structures do not have identity then they have no identity graph associated with them, this property is a major difference between the identity graph of groups and that of the other algebraic structures the studied. Motivated by the work of Yalcin and Kirgil studied the identity graphs of finite cyclic groups, they examined the identity graph using the self-inverse and mutual inverse elements of the finite cyclic groups, to determine the number of triangles and edges contained in the graph [1,3].
Similarly, Kelarev and Quinn studied the directed power graph of semi group; they defined the directed power graphs of finite groups and studied their combinatorial properties [2,4]. However, the undirected power graph was introduced by Chakra arty they characterized the class of semi groups with a connected or complete power graph. Subsequently, the power graph of algebraic structures became an interesting focus in the literature see, for example [5-12]. Meanwhile, Chattopadhyay and Panigrahi attempt to solve an open problem of Abawajy, Kelarev and Chowdhury [6] observed some relationships between the power graphs and coyly graphs of finite cyclic groups [6,13]. For instance, they showed that, the vertex deleted sub graphs of some power graphs are equal to the spanning sub graphs and complement of vertex deleted sub graphs of Cayley graphs. In this paper, our primary objective is to merge the algebraic properties of identity and power graphs of finite groups to have the identity-power graph of finite group, thereafter, the combinatorial properties of the identity- power graph will be determine up to isomorphism. Besides, the motivation for this study is ideas of Kandasamy and Smarandache to study the identity-zero combined graph of a semi group S to compare the zero divisor graph to the identity graph of semi groups and the work of Ma and Su who used the algebraic properties of order super graph and power graph to study finite groups. In the same vein, we use the algebraic properties of identity graph and power graphs to construct the identity-power graph of finite groups [1,14].
Basic prerequisites
Human In this section, we state some graph theoretic terminologies and some known results which have been used in the main results of this study, furthermore, these terminologies will help in better understanding of this paper. All graphs considered in the main results are simple graphs; the graphs are without loops or multiple edges. For the definitions of the basic terms and results given in this section see [8,9,15-17].
A graph Γ is a combinatorial structure formed by finite non-empty set (V,E), where V is the set of vertices viewed as points and E is the set of edges viewed as line joining the points. The cardinality of V (Γ) is called the order Γ while the cardinality of E (Γ) is called the size of Γ. The degree of a vertex x in a graph Γ denoted by δ(x) is the number of edges incident to it. That is the number of edges or arcs connecting x. A graph is said to have parallel edges if there are more than one edge which join the some pair of distinct vertices. A loop on the other hand is an edge that joins a vertex to itself while a walk of length k n in a graph Γ with vertex set V (Γ) consist of an alternating sequence of vertices and edges consecutive elements of which are incident, that begins and ends with a vertex.
Definition 2.1: Let G be a finite group, the identity graph of G is a simple undirected graph in which the vertex set is G itself, and two distinct vertices x and y are adjacent if and only if xy=e or yx=e, where e is the identity of G [1].
Definition 2.2: Let G be a finite group, the power graph of G is a graph with vertex set G and two distinct x,y ∈ G are adjacent if x=yn or y=xn for some n ∈ N [8].
Definition 2.3: Let a be an arbitrary element of a finite group G and let e be identity If a=a−1, then a ∈ G is called a self-inverse element of G denoted by S (G) [18].
Definition 2.4: Let a be an arbitrary element of a finite group G and let e be identity. If there exist a
b ∈ G such that ab=ba=e, then a ∈ G is called a mutual inverse element of G denoted by M(G) [18].
Corollary 2.5: Let G be a finite group, then |S (G)| and |M (G)| are both even [18].
Remark 2.6: Let G be a non-cyclic group, then |SG)| ≥ 2.
Corollary 2.7: Let G be a finite group of odd order, then |S (G)|=1 and |M (G)|=|G|-1 [18].
Theorem 2.8: Let G be a finite group, then |S (G)| is equal to 1 if |G| is odd and |S (G)| is equal to 2 if |G| is Even [18].
Definition 2.9: A graph Γ is said to be complete if there is an edge between every pair of distinct vertices in Γ. On the other hand, Γ is said to be connected if there is a path between every distinct vertices in Γ [16].
Theorem 2.10: A given connected graph G is an Euler graph if and only if all the vertices of G are of even degree [16].
Definition 2.11: In graph theory, a regular graph is a graph where each vertex has the same number of neighbors, i.e. every vertex has the same degree or valency a regular graph can be an x-regular graph where every vertex of the graph has the same degree x [16].
Definition 2.12: Let G be a finite group, the order of an element a € G, sometimes called period length or period of a,is the smallest positive integer m such that am=e (Where e denotes the identity element of the group, and am denotes the product of m copies of a). If no such m exists, G a is said to have an infinite order [9].
Definition 2.13: Let Sn be a symmetry group, π ∈ Sn (n>3) is called and involution if π=π−1. That is, if π* π−1=e, where e is the identity permutation of Sn. The set of involution permutations is denoted by I (π) [19].
This article has studied the identity-power graphs of finite groups, clearly we show that the identity-power graph Γ (G) of a finite group G is never complete and the number of isolated vertices on the identity-power graph of G is greater or equal to 2. We also show that if every element x in the finite group G has a unique inverse y G, and then the identity-power graph of G is an acyclic graph. Further research is encouraged to find other properties of the identity-power graphs of other algebraic structures.
The authors sincerely thank the anonymous referees for their careful reading, con- structure comments and fruitful suggestions that substantially improved this article.
Physical Mathematics received 686 citations as per Google Scholar report
