Optimal Placement of Multi Actuators in Active Control of Building Frames

Rajshree Charan^1*, Shrimali MK² and Bhart SD^2
*Correspondence: Rajshree Charan, The Maharaja Sayajirao University of Baroda, Vadodara, India, Tel: + 9409236669, Email:

Keywords

Active control • Earthquake • ANN • Base shear • Top storey displacement • Control force

Introduction

The optimal placements of actuators in a ten storey building frame for a maximum number of three actuators are presented using the method of trail. Three cases of actuator placement are considered, namely, one actuator, two actuators and three actuators. The response quantities of interest are the top floor displacement, the maximum inter storey drift and the maximum base shear. The optimal reduction in responses for these quantities is obtained for four real earthquakes, namely, Kobe, Spitak, Elcentro and Bhuj. LQR algorithm is used to obtain the controlled responses.

The classical control theory is based on the frequency domain analysis employing transfer function approaches. A major limitation of the theory was the use of single-input single-output methods. Modern control theory is based on time domain analysis expressed by first order differential Equations utilizing state space representation [1].

Theory and Experimentation

Linear quadratic regulator (LQR)

In classical linear optimal control, the control force is assumed to be a linear function of the state vector and the control of the responses is obtained by minimizing a quadratic performance function. Therefore, it is popularly known as a linear quadratic regulator (LQR) control. Assuming the state vector to be zero at time t = 0, the performance index is defined as

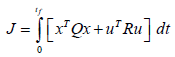(1.1)

In which, tf is the duration of the earthquake excitation; Q is a 2n X 2n semi-definite matrix and R is a n X m positive definite matrices. The matrices Q and R are termed weighting matrices. The relative values of the elements of the matrices are selected according to the importance attached to the different parameters of control. For example, large values of the elements of Q compared with those of R denote that reduction of response is given more weightage at the cost of control force. The opposite is indicated when the elements of R are relatively large. Similarly, in the Q matrix, relatively large values of the diagonal elements corresponding to the displacement response denote that the velocity response is penalized in the minimization procedure [2].

The LQR estimates the control force by minimizing the quadratic cost function. For a continuous-time linear system defined on t ∈ [t₀, t₁], the Equation of motion written in state space form is-

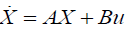(1.2)

With a quadratic cost function defined as

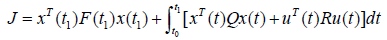(1.3)

The feedback control law that minimizes the value of the cost is

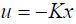(1.4)

Where, K is given by

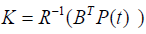(1.5)

And P is found by solving the continuous time Riccati differential Equation

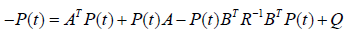(1.6)

From Equation (1.4), it is clear that the time histories of controlled response and the control force are such that they provide a minimum value for the performance index J. Furthermore, the Equation (1.5) shows that the performance index J is in a way equivalent to the total energy of the system, including that of the external force over the entire duration of the excitation. Thus, the control algorithm in some sense obtains the control force by minimizing the total energy of the system over the duration of the excitation. This algorithm is known as a linear quadratic regulator (LQR) algorithm as the control force is a linear function of the state vector and the performance function is a quadratic function of the state variable and the control force. Figure 1 shows the Simulink block diagram for LQR.

To investigate the effectiveness of the control system for different excitations, four time histories of ground motion are selected for numerical simulations, namely, Bhuj, Elcentro, Spitak and Kobe (Table 1).

The control and uncontrolled responses of the frame are obtained for each earthquake. The peak control force required for obtaining the optimal response is recorded and shown along with the percentage reduction of responses. The method of trail consists of placing the actuator at different floors and plotting the percentage reduction in each case [3].

The optimum control with one actuator

The percentage reduction in the maximum base shear (B.S.), the peak top floor displacement (TFD) and the maximum interstory drift (DRIFT) for different placements of the actuator are observed. The results are presented in the form of three types of plots, namely,

i. The variation of the percentage of reduction in the response quantities of interest with the position of the actuator;

ii. The variation of R factor with the position of the actuator and

iii. The variation of normalized maximum control force with the position of the actuator.

‘R’ is defined as the ratio of the percentage reduction in the response quantity of interest per unit peak control force, expressed as a percentage of the total building weight. The variations are shown for four different earthquakes, i.e., Bhuj, Elcentro, Kobe and Spitak.

It is seen from the figures that the variation of the percentage reductions in the peak top storey displacement and the maximum interstory drift increase as the actuator is placed on higher floors. The maximum percentage reductions for the two responses are 57% and 50% for Bhuj earthquake; 48% and 41% for Kobe earthquake; 73% and 66% for Elcentro earthquake and 63% and 55% for Spitak earthquake [4].

The response reduction with two actuators

In the case of optimal control with two actuators, different combinations of placement of actuators are attempted. The combinations are shown in Table 2.

The response reduction with three actuators

In the case of optimal control with three actuators, different combinations for placement of actuators are attempted. The combinations are shown in Table 3 below.

Eight combinations are attempted for investing the optimum percentage reduction in response expressed as a factor R i.e., percentage reduction per unit control force. The variation in the value of R with the different combinations of three actuator position shows a similar trend as that of a single actuator and two actuators for the combinations considered in the study of the different earthquakes. However, when the variation of the percentage reduction in response quantities with different combinations of actuator placement is plotted separately, without any consideration to the peak control force, the variations are different than the variation of R factor with the actuator combination as can be seen from the following figures [5].

The peak control forces required for three cases of actuator placement, one actuator, two actuators and three actuators are shown in Table 4 below.

It is seen from the Table 5 that peak control force requirement does not significantly differ with the number of actuators used. However, there is a significant change in percentage reduction of responses. Further, it may be noted that peak control force increases with the increase in peak ground acceleration of an earthquake, as expected [6-9] (Tables 6-8).

Discussion and Conclusion

Optimal placement of actuators in 10 storey building frame is investigated using a trial approach for 4 real earthquakes having different peak ground acceleration values. 3 cases are studied, namely,

i. Placement of only one actuator

ii. A combination of two actuators placed at two different floors and

iii. A combination of three actuators placed on three different floors.

The optimal placements are selected based on the percentage reduction of three response quantities, namely, peak top floor displacement, maximum inter-storey drift and maximum base shear. Control responses are obtained using LQR algorithm. Optimal positions are investigated by considering

i. Percentage reduction in response alone

ii. Percentage reduction / unit peak control force, R factor and

iii. By specifying an upper limit for the peak control force that can be accommodated in actuator.

The numerical study leads to the following conclusions:

1. For the single actuator, peak top floor displacement and max inter storey drift increase as the actuator is placed at higher floor. The max reductions are achieved when the actuator is placed on the 10^th floor.

2. For the base shear, the pattern of variation is opposite to those of max top floor displacement and max inters storey drift.

3. The variation of peak control force has the same trend as that of percentage reduction in base shear.

4. The variation of the R factor (percentage reduction/unit control force.) is of the same nature as that of percentage reduction in responses for peak top floor displacement and max base shear. However, this variation of base shear is different from the percentage reduction of responses, in the case of Bhuj earthquake.

5. Therefore, it shows that optimal positions of the actuator may be different for different criteria used. Here, they are decided based on a percentage reduction of response alone and percentage reduction per unit control force.

6. In the case of two actuators and three actuators placed in the frame, the trend of results remains the same as that of single actuator.

7. Higher percentage reduction in responses can be achieved by increasing the number of actuators to control, as expected. However, considerable reduction in response can be achieved with single actuator also.

8. The max control force required to control the responses increases with increase in PGA level of the earthquake. The max control force does not change significantly with the number of actuators used. However, percentage reduction in responses changes significantly with the number of actuators used.

References

1. Tongpadungrod P, TDL Rhys, and PN Brett. "An approach to optimize the critical sensor locations in one-dimensional novel distributive tactile surface to maximize performance." Sensors and Actuators: Physical 105 (2003): 47-54.
2. Soong, TT. “Active structural control in civil engineering.” National Centre for Earthquake Engineering Research (1987).
3. Soong, TT, Masri SF, and Housner GW. “An overview of active structural control under seismic loads.” Earthquake Spectra 7 (1991): 483-505.
4. Spencer, Billie F and Nagarajaiah Satish. “State of the art of structural control.” J. Struct Eng 129 (2003): 845-856.
5. Singh, Mahendra P and Moreschi Luis M. "Optimal placement of dampers for passive response control." Earthq Eng Struct Dyn 31 (2002): 955-976.
6. Pantelides, CP. "Optimum Design of Actively Controlled Structures" Earthquake Engrg. Structural Dynamics 19 (1990):  583-596.
7. Fisco NR and Adeli H. “Smart structures: Part I—Active and semi-active control.” Scientia Iranica 18 (2011): 275-284.
8. https://www.chaocompute.com/wp-content/uploads/2020/07/Dynamics-of-Structures-Clough-Penzien.pdf
9. Datta, TK. "A state-of-the-art review on active control of structures". ISET J Earthq tech 40 (2003):1-17.