Optimized Train Dispatching and Rescheduling During a Disruption in a Bottleneck Section

Danson Byegon^*, Sosina M Gashaw and Birhanu Reesom Bisrat
^*Correspondence: Danson Byegon, Department of Environmental Engineering, Addis Ababa Institute of Technology, Addis Ababa, Ethiopia, Tel: 251942279643, Email:

Keywords

Delays • Disruptions • Infrastructure • Optimization • Scheduling • Train dispatching

Introduction

  From railway planning and operational point of view, research towards the development of optimal dispatching model for the transportation industry is deemed indispensable. Railway transportation is deemed to be one of the most reliable, efficient, sustainable and competitive mode of transport as compared to other means.

Despite these merits, at times the trains might not always arrive and depart as scheduled or even sometimes train operations are even cancelled due to uncertain and unforeseen events which can be attributed to external or internal failures in the railway system such as railway line derailment, severe weather conditions, locomotive breakdowns etc., this events may lead to underutilization of the available railway infrastructure. In such situations, Train dispatchers need to put in place some mitigation measures such as reordering the trains movements and routes utilization, rescheduling of train plans and retiming within a very short time to avoid impacts of delays caused from spreading further and avert conflicting route scenario from occurring.

During severe disruptions, the stopping pattern of some trains may also be changed to offer more options to the disrupted passengers to travel to their destinations [1,2]. The rescheduling activities should be done in a manner which considers passenger weights and distributions along the platforms and the allocation priorities given to the highly demanded trains basing on such factors like passenger demand and general passenger flow, other remedies to optimize operations in case of a disruption includes insertion of train services and even cancelations.

Delays encountered in railway systems can be categorized as either primary or secondary delays. Warg et al. defines Primary delays as the types of delays affecting a particular train schedule and those delays are not as a result of malfunction of other trains using the line. Whereas secondary delays are defined as the delays caused by earlier delays of other trains within the network sharing the same infrastructures, passenger transfers, transfers and reallocation of crew and rolling stock connections among others [3].

In solving resultant conflicts by train dispatcher; simple, reliable and efficient cost effective model needs to be defined and employed. This dispatching model will be helpful for dispatchers in ensuring that they make reliable decisions within a very short time frame and ensuring that there are no conflicting route scenarios. A lot of efforts have been put in place in regards to solving train dispatching or scheduling and rescheduling problems, however, the preference of use of railway system is increasing in demand and thus requires better solutions to achieve more reliable railway systems.

This article focuses on the integration problems associated with train rescheduling, train reassignment under multiple disruptions in a railway system particularly in a constricted or a “bottleneck” section, timetabling and delays experienced to come up with an optimum dispatching model to achieve the best use of the available infrastructure with minimal delays.

Literature Review

Problem description

Figure 1 below shows a disrupted route network, there are two disruptions which occur concurrently along the route, the causes of the disruptions could be different and uncertain or same causes of disruption but generally it affects the smooth flow and routine operations of the trains. To have a clear understanding of the context, we consider n number trains using the route as shown above, the trains are given the notations T1,T2,T3,T4,Txn,Tyn respectively. The track network has 4 stations in total with notation subscript X for the stations along eastwards flow route and script Y for the stations along westwards direction flow.

The disruptions in the problem illustration, occurring in the line affects the scheduling operations and propagates the delays, for example, the train T3 cannot be dispatched from station By until the train T1 has passed through the disrupted section and a certain clearance time has been covered. To solve this problem, possible solutions would be rescheduling, reordering or even cancelling some train operations, any of the approach chosen should have sensible economical cost benefit resolutions and proper priority considerations.

The Bottleneck sections of mainline railways are usually characterized by high density traffic with many resource requests, where a disturbance from one single train could result in heavy impactful delays across a number of trains, multiple disruptions occurring concurrently in the busy section will in fact have detrimental impacts if no mitigation measures are taken may lead to underutilization of its infrastructural capacity and unprecedented delays. The model formulation is constrained to ensure that such conflicting situations does not occur after rescheduling the trains track allocations. Figure 2 presented below access the impact of disruption on a normal traffic flow.

A train i moving from station A to station E is shown in the Figure 2 above, the first blue line shows the movement of the train i as guided by the scheduled time table, whereas the orange line represents the rescheduled movement of the same train i in a path having multiple disruptions occurring between stations A,B,C and D, the duration of the disruptions are not uniform as shown by the time delays each train has to wait in the disrupted section, this shows the uncertainty index and weight of the disruption.

Related work

Train dispatching optimization is one of the fields of interest in terms of railway planning and operations and it has attracted extensive research in past few decades; several optimization models have been proposed, some of the cutting edge solutions proposed includes: Demand forecasting modules, discrete event simulation models, integrated models, multiple agent system, linear programming models and computer aided dispatching systems among others.

A number of previous works done on train dispatching problems has been able to assist in trying to solve problems faced by train dispatchers optimally. Some of the earliest works uses linear programming model and mixed integer linear programming as discussed by Higgins et al. in determining the best crossing and overtaking positions for trains on a single line track using fixed velocities and departure times of the trains [4]. Later on, a computer aided dispatching system for generating effective train schedules on single-line track using branch and bound algorithm was formulated. In addition, a high level petri nets simulation model that detects and manages train path conflicts on a single track railway line is presented by Jeremic D, et al. [5].

Over time several dispatching models have been developed employing greedy approach (heuristic method) in solving dispatching problems for timetabling and dispatching trains on single line track, heuristic algorithm for solving conflicts encountered by trains on single-line track that appear in time; Afeez et al. and Shakibayifar et al. proposed detailed information on the implementation of different heuristic algorithms for train dispatchers in solving train dispatching problems [6,7].

Bettineli et al. furthermore proposed a fast and effective parallel algorithm that is based on an iterated greedy scheduling of trains on a time space network [8]. Given a disturbed railway operations or timetable, a real time train dispatching and rescheduling solutions are suggested by Ariano et al. and who designed a dispatching system of decision support system for traffic controllers. Khwanpruk et al. also proposed a Timetable Optimizer (TO) consisting of demand forecasting module, train optimization module and timetable generator module [9,10]. Whereas developed a discrete event simulation model that employs a variable neighbourhood search algorithm to maintain the service level under infrastructure elements’ unavailability [11,12].

Due to the unpredictable nature of the incidents, the uncertainty associated with obstruction duration was experimentally analyzed through probabilistic scenarios. Barbour et al. proposed a methodological tool set, called the dispatch analysis problem that can analyse recent, empirical train dispatching data against an optimal dispatching plan [13]. In his work, Wang et al. presented an integrated model to optimize the train schedule and circulation plan simultaneously based on a given service pattern generated by the demand analysis and line planning [14].

Furthermore, Josyula et al. presented a parallel algorithm to efficiently solve the real time railway rescheduling problem on a multicore parallel architecture [15]. With the aim of improving simulation efficiency by directly confirming the next discrete time, Zhang et al. focused on discrete dynamic optimization on train rescheduling on single-track railway with the consideration of train punctuality and station satisfaction degree [16]. Takagi et al. also proposed the use of a Genetic Algorithm (GA) with Object Oriented Multi Train Simulator (OOMTS) developed by Birmingham University, as an embedded simulator to optimize the order of route setting [17].

Wang et al. and Gong et al. studied an integrated train rescheduling and rolling stock circulation planning problem for the complete blockage situations in a metro line, by modelling the problem as a complex multi-objective MILP formulation [18,19]. Withal Leonardo et al. also suggested the formulation of a mixed integer linear programming model using Benders'-like decomposition approach to minimize the number of (heavily) delayed trains in cases of disruptions [20]. Guo et al. proposed a Multi-Agent System (MAS) to reduce rail transit energy consumption when disturbances occur. Furthermore, Huang et al also discussed three models in a progressive fashion to optimize the last train timetable incorporating multimodal coordination.

Railway traffic management

There is a need to offer quick railway traffic rescheduling to ensure least disturbance along the line operations when a disruption occurs. One of the mitigation measures to this problem was proposed by Shakibayifar et al. who designed a simulation based optimization model that incorporated dynamic dispatch priority rules with the objective of minimizing the total delay time of trains and a variable neighbourhood search meta-heuristic.

A railway transport system is a very complex system with integration of human controls and behavior, technical devices, and external environment integrated together and thus contains many risks of disturbances. Railway traffic performance are usually managed by a carefully designed plan of operations also referred to as train timetable, the timetable which incorporates orders and the timing of the trains several months in advance is referred to as offline timetable. There is however usually a secondary remedy to offer real time measures to manage traffic in cases of disturbances.

Railway bottleneck

A bottleneck section is a section in a railway network consisting of two or more junctions points at each end and it is usually a very busy section as many trains going in different direction uses the section. This definition of the bottleneck shall be used in our problem modelling in the subsequent sections of this paper. The rescheduling of approaching trains for one portal junction needs, therefore, to consider the movements of the trains approaching this portal junction from another portal junction, looked at the junction designs and efficiency.

Railway timetabling

A timetable is the foundation of any public transportation system. It is critical in determining the paths or routes to be taken and the travel times from the points of origins to the desired destinations. Designing of train timetable is a complex process which must take into consideration the feasible infrastructural capacity, safety assurance, and resource constraints. The extent to which disturbances such as delays propagate through the system is highly depends on the robustness of the timetable.

The urge to come up with a good and reliable timetable has triggered many researchers to study route planning and the field of public transport optimization Lieshout et al. Rail traffic planning process involves strategic and tactical levels. Strategic planning entails railway network planning and line planning. Whereas, tactical level is aimed at ensuring efficiency and reliability and it entails timetabling, rolling stock planning and crew scheduling.

Railway timetables can be grouped into two categories as described by Gao et al. namely:

• A regular timetable which allows passengers to easily remember the exact departure times at stations.

• An irregular timetable, which can better match passenger demand and reduce operating costs and minimize passengers’ cost for their trips, and enhance passengers train-travel experience Xie et al. Skip-stop plan; is a strategy commonly used to increase vehicle speeds and reduce passengers travel times as explained by Mei et al. and Tang et al.

Route disturbance

Railway traffic is operated according to a detailed off-line plan of operations, specifying for each train its path through the network plus arrival and departure times at its scheduled stops and studied how to support dispatchers in the management of infrastructure disruptions by considering a seriously disturbed traffic conditions on double track railway lines where some block sections of one track are unavailable for traffic, e.g., due to a temporary track blockage.

In emergency perturbations occurrence, there is strict time limit feasibly available to compute a new timetable to satisfactorily gather for all the rail network needs particularly if the perturbation occurs on a very busy section and in most of the cases operators usually restrict themselves mostly to a few manual modifications of the timetable. Ariano et al. looks into how network dispatchers regulate the railway traffic. Existing dispatching systems are able to provide viable solutions only for small instances or for simple perturbations. However, the real-time traffic management is still under the control of human dispatchers, in most cases, who usually do not have precise information about the future evolution of train traffic and the chosen traffic control actions may be often sub-optimal.

Train rescheduling

A scheduler is used to generate feasible timetable for the railroad system, it allocates departure and arrival times for all trains within the network and also tracks needed for their journeys. Some of the major scheduling constraints are described in and they include; speed constraints ensures that a trains within the network should not exceed the maximum allowed or maximum safe speed specified for it to use on any track during their journey. Furthermore, station entrance constraints ensure that there must exist fixed time interval between two trains arriving a stations using same track line. Whereas, load or weight constraints checks on the weight of the locomotives and ensures that the weight of trains specified to run on any track within the network must not exceed the maximum allowed weight resistance of that track.

Timetable conflicts may occur when the trains within the network does not abide by the scheduling rules, possible causes of these problems can be breakdown of trains or stochastic events. Possible timetable conflicts are discussed by and are describes as; trains meeting conflict, station capacity conflict and trains headway conflict. These conflicts can cause problems within the network and needs to be solved to avoid accidents (Table 1).

Rescheduling model development

Train rescheduling during a disruption is considered to be one of efficient mitigation remedy to ensure that train services continue operating using the available feasible routes, even though it can be a very complex and challenging task. The rescheduling model formulated for this purpose is a mathematical model as discussed below.

Mathematical model formulation

A mathematical model can be so helpful in coming up with an efficient and reliable rescheduling solution. In formulating a mathematical model; the first step creating a conceptual mathematical model that captures the important resources and constraints in the train dispatching and routing problem. The conceptual mathematical model can then be translated into a computer program that builds that model and solve the model using a math programming solvers (Tables 2-4).

Notations:

Conceptual mathematical model entails:

• A set of decision variables, which capture the range of possible decisions to be considered are defined.

• A set of constraints, which capture global limits on the values of the decision variables are defined.

• An objective functions on the decision variables that captures the value to be minimized or maximized.

In creating a mathematical model to offer optimum rescheduling operations, the problem illustration in Figure 1 above is considered, the objective function is to minimize total train delay time, the constraints and other parameters such as decision variables shall be discussed in subsequent sections:

The diagrammatic representation of steps in optimization model development is shown in Figure 3 below.

Parameters terms definitions:

• Routes/Available blocks: Feasible routes in the disrupted section represented by blocks represented by b1, b2, b3, b4.

• Trains: Trains waiting to use the disrupted section represented by Q_ix, Q_iy. i.e. train i.

• Trains speed: The permissible speed profile allowable in the disrupted section i.e. Vd and actual train speed during normal operations, i.e. Vr.

• Direction: The directional flow provisions of the trains. Eastwards directional flow is named X direction and westwards directional flow is named Y direction.

• Passenger and priority train allocation weights: Represented by Wp.

• Number of disruptions: represented as μ_k.

• Weight μk: Impact of the disruptions on the routine trains operations and timetable plan.

• Clearance time: It is the time the trains will have to wait for the feasible route to be available for their use, i.e. the time it will take a train currently occupying a given route section to clear off.

• Weight q: Maximum number of trains waiting to use the available route in the disrupted bottleneck junction section.

• Station dwell time: The time a train will stop at a given station for the passengers to board or alight from the train; this is determined by the passengers’ distribution weights.

• Scheduled Time (S_t): specifies the minimum running time (computed prior to the problem solving) i.e. scheduled running time for event k if event k is an event for a segment between stations.

Decision variables

• Assigning route r to event E if train i request to use the section p_i,E,1= ε {0, 1}; 1 if event E of train i uses the route section r; 0 otherwise.

• Select route r for set qi trains ϵ {0, 1}; 1 if the minimum safety headway t_mH constraints, speed constraints (v), time constraints (t) and directional constraints G; are met; 0 otherwise.

• Assign qi, r ϵ {0, 1}; 1 if there is feasible route r available for trains s et q, clearance time provisions are met and only if there is no conflicting route scenarios; 0 otherwise.

• Vrij=Actual speed of train i using the feasible route indexed by j.

• Δj=Minimum clearance time for the trains moving in different directions to complete using the section so that the section can be available for use by other trains moving in different directions.

• For each event (i, k,) ϵ Mj, we have the decision variables pi, k,1, pi, k,2,… pi, k,n, where pi, k,1 is a binary variable that specifies whether route r (associated with j) is used by event E of train i.

Objective function

The objective function is to minimize the total time delays encountered by the trains using the disrupted section of the bottleneck junction (i.e. the sum of the final delays when trains arrive at their final destination), which is represented in equation (1) below.

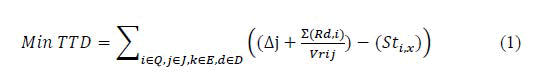
No wait constraint: This constraint ensures that the resource allocations start immediately the previous one ends.

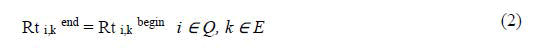
Direction constraints: This constraint serves to balance the traffic flow in the disrupted section to ensure that the flow is balanced in both directions while taking into account the priority considerations.

The directional constraints can be equated as:

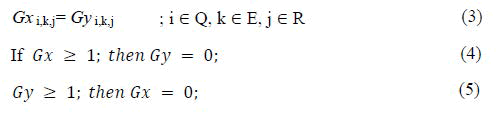
Run time and dwell time constraints: This constraint ensures that the new event starts after the running time and the station dwell time of the previous event has been completed.

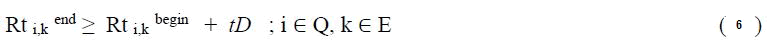
The running time of the train within a particular section of the railway is guided by the availability of feasible route with no other train using the section at the time of allocation.

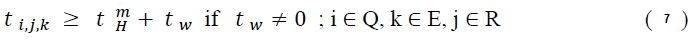
Running time check: The main task of the running time check is to find the invalid solution individuals that do not satisfy the running time restriction shown in equation (8)

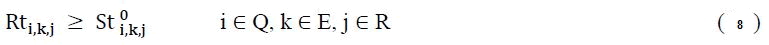
The running time check rule is shown in equation (9) below; If

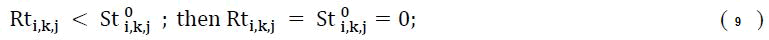
At the moment of disruption, if the train is still not dispatched from the origin, it must satisfy the departure time interval from the origin. This is represented in the constraint below:

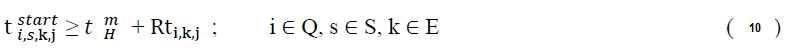
The travel time (or stop time) of the trains in the block (or station) are variable but should be defined by the minimum and maximum ranges

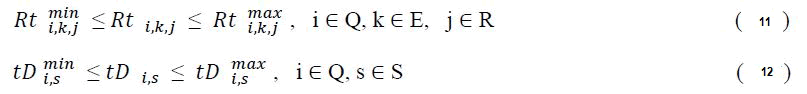
Track occupancy constraint: This constraint ensures that one train occupies a particular route section at any given time. This can be expressed as;

Route constraints: The trains can only proceed if there is no conflicting routes scenario.

If a single-track section is blocked, then the arrival time to the block for all incoming trains should be after the completion time of the blockage (t1+τ1) i.e.

If the blockage occurred in one of the lines of a double-track block section, then during the disturbance, and the partial service is accepted. This is expressed by the constraints below:

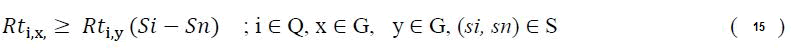
Where Sn is the next station after disruption point and Si is the station before disruption point.

The route setting control sequence can be defined as follows, using 0 and 1 to denote the two possible routings i.e. 1 show that there is a feasible route and 0 shows that there is no feasible route.

Routes in eastwards direction is represented by X and the routes in the westwards direction is represented by Y.

For the eastwards direction:

For the westwards direction:

To ensure that not more than two routes is allocated to one train i, the constraints equation (22) and (23) implements that condition

Optimal route setting for train i can be summarized as shown in equation (24) below

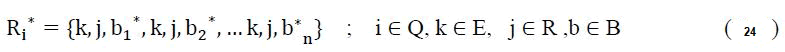
Headway constraints: The constraint ensures that the trains moving in the same direction must stick to the safe minimum headway requirements for safety purposes.

The minimum safety headway must not be exceeded.

.

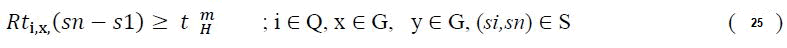Rt_ix(sn-s1) is the running time of train i two subsequent blocks or stop overs i.e. stations Sn and S1.

Sequence and headway admissibility check: This constraint is used to ensure that solution individuals generated by the stochastic algorithm are valid in terms of the train sequence restriction at control boundaries. For example, if there is only one route for trains from point A to point B, then the train arrival sequence at point B must be the same as that at point A.

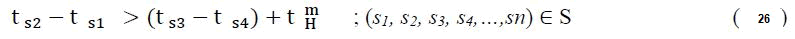
t _s2-t _s1 is the time taken between station s2 and station s1,(t_s3−t_s4) is the time taken by train between station s3 and s4.

Speed constraints: This constraint ensures that the maximum allowable speed profiles must not be exceeded. There is maximum allowable speed of the trains when running in the disrupted section must not be exceeded due to curvatures i.e.

Vr ≤ max permisible speed (Vp)

The speed of the train must also no be lower than a certain allowable threshold speed in order to utilize the infrastructure capacity in a relatively optimal manner.

Therefore, considering the two speed conditions, the speed constraint is presented as;

vp_min is minimum allowable speed for the train to cruise on the track.

For this particular formulation, there are some time delays which we assumed to be negligible and are not exclusively calculated, i.e. the time taken in setting and resetting the switch points, as well as stochastically varying delays at the stations which might be attributed to dwell time inconsistencies, we consider this time delays as very minimal and thus inconsequential in the overall delay encountered by the train running through the disrupted section.

To solve the complete MILP problem presented above (composed of objective function (1) and constraints presented in the subsequent equations from equation (2) to equation (27), may require a lot of computational effort to simply this, the absolute term in the objective function can be linearized.

Validation test scenarios

To validate the formulated mathematical model, multiple disruptions scenarios occurring in the rail network are considered. For this purpose, a numerical example is used. Assume a rail network as illustrated in Figure 4 below.

The first and the second disruptions are induced in the segments between stations STx1 and STx2 and between stations STy3 and STy2 respectively in different directions. The third disruption happens between stations STx3 and STx4. The disturbance periods vary i.e. the first disruption starts at time T1 and the second disruption starts at time T2 and the duration of each disruption is

τ1 and τ2 respectively. The data required for numerical experiments is presented in subsequent sections. The departure time tolerance has been defined in order to achieve the best initial plan. However, in this example, the choice of departure time interval is arbitrary.

Without loss of generality, it is assumed that the segment distances are equal i.e. stations are 1 KM apart from each other. The running time between adjacent stations is calculated using velocity time formula taking into consideration speed limits restrictions and the network is a double rail and each section has switches and two rail tracks that permit trains to cross as illustrated in Figure 4 above.

The problems presented above are typical hybrid optimization problem that includes continuous variables (train arrival time) and discrete variables (route setting decisions). The discrete route setting decisions are identified once availability of a feasible route has been confirmed. If there are constraints for the train sequence on the converging routes, the route setting at the junction point must be decided on the basis of the train sequence demands. Also, the calculation of the train arrival time must take into account the route setting constraints.

Results and Discussion

Scheduled train timetable

The scheduled plan of the train operations during normal network operations without a disruption is presented in the state space chart below:

Figure 5 above show the movements of trains under normal scenario when there is no disruption, there are eight trains represented by the color codes and a total of six stations denoted by ST. The upstream graphical representation shows the trains moving in eastwards direction and the downstream graphical representation show the trains moving in westwards direction. During normal trains operations, the traffic flow is smooth and the traffic movements are guided by the scheduled timetable.

Disrupted route scenario

Due to the uncertain nature of the disruptions, different possibilities for the start time, duration of delay and the location of the disturbance are probable. Different disruption scenarios are induced in the network for this purpose, the induced disruptions are shown in Table 5 below. A case of a single and double disruptions scenarios is considered, with a the pair of double disruptions occurring concurrently, and the disruption starts just before the most congested periods of the day, in the bottlenecks with the highest traffic as computed by a traffic congestion factor defined as the number of train conflicts in a schedule during a specified interval.

Choice of the algorithm

Matlab optimization algorithms i.e. Fmincon solver and genetic algorithm are used to optimize the continuous real time train arrivals during different disruption scenarios compared to scheduled arrivals times and their performance compared, taking into account the objective function, defined constraints and discrete route setting decisions variables.

Comparison between Fmincon and GA Solvers optimization during different disruption scenarios.

The performance and robustness of the two algorithms used are compared in Figure 6 and it is noted that Fmincon solver algorithm and GA solver offers almost similar optimal results in terms of simple or single disruption scenarios although there is some small variance. Whereas, for multiple and more complex perturbation cases i.e. D1D2, D1D3, D2D3 and D1D2D3, GA solver offers better results as compared to Fmincon solver, this is attributed to the nature in which the two solvers approach and defines the problem; Fmincon solver applies the use of a Successive Quadratic Programming (SQP) method. In this method, a Quadratic Programming (QP) sub problem is solved at each iteration.

Genetic algorithm offers a global search solution beginning with a randomly chosen assortment of chromosomes, which serves as the first generation (initial population). Then each chromosome in the population is evaluated by the fitness function to test how well it solves the problem at hand. Now the selection operator chooses some of the chromosomes for reproduction based on a probability distribution defined by the user. The fitter a chromosome is, the more likely it is to be selected. This explains better performance and robustness of GA algorithm in a complex and uncertain disruptions.

Optimized reschedule during a single disruption

Figure 7 presented below show optimized trains movements in case of a single disruption occurring in a rail network, the Disruption case occurred between station STx1 and STx2 (Tables 6 and 7).

Optimized reschedule in a case of double disruption: Figure 8 presented below show an optimized trains movements in case of double disruptions occurring in a rail network, the disruption cases occurs between station ST1 and ST2 and between ST3 and ST4 respectively with different start times and different disruption durations as shown graphically below. It can be seen that the train takes a longer time to move through the disrupted section as compared to unperturbed sections.

For this particular study, seven different random disruption scenarios presented in Table 3 are used to evaluate the mathematical model designed. Tables 6-7 above shows the optimal schedules for each train and optimized variable parameters respectively in each case scenario, the objective value for each disruption scenario is obtained.

Figure 5 shows a train traffic flow during normal operating conditions when there is no disruption, whereas Figure 7 and 8 shows a traffic flow state space graph during a single and double disruption respectively. From the observation in both cases, it is observed that more total travel time delays are encountered for the highly disrupted scenario with multiple disruptions as there are few feasible routes with main trains requesting to use the available resource. It is also observed that the nature and the location of the disruption along the railway line have an impact on the total time delays. The performance and robustness of the two algorithms used are compared in Figure 6.

Conclusion

In conclusion, a mathematical model that is able to minimize the total delay time is designed and tested, the results shows that the model is able to achieve its objective by adjusting and offering optimal time delays for each individual parameter contributing to the total train time delays for the train using the disrupted section, the model is also able to offer a rescheduled plan in a case of a single or multiple disruptions occurring concurrently at the railway network.

A small delay resulting from a single train or a simple disruption can result to massive impacts when it comes to utilization of the available railway capacity, the disruptions could be as a result of mechanical failures, power outages, derailments, accidents and even other uncertain and unprecedented causes, this disruptions generally alters the normal operational plans in terms of time table scheduling, passengers and freight transportations, therefore to mitigate the impact of this disruptions, there is need to minimize time delays resulting from the mentioned disruption. This article developed and validated a mathematical model to minimize time delays from the resultant disruption, the results from the validation confirms that the model offers a fast rescheduling and route allocation approach with minimized total weighted delays.

This model furthermore compares solutions using two different algorithms and from the results, there is no much variance in terms of the best solutions however each algorithm approaches the problem differently i.e. Fmincon solver looks at the scalar variables with respect to the constraints whereas the genetic algorithm solver modify the problem into a population approach and offers its search solutions using mutation approach, genetic algorithm is found to offer more optimal solutions in a context of a global problem search, whereas Fmincon solver is suitable when solving linear scalar problems.

It is recommended that the railway engineers should design and incorporate switch points at appropriate locations between the bottleneck sections to enable trains change of tracks in case of unprecedented disruptions so as to offer alternative feasible routes for the trains.

The future study aims at using artificial intelligence to offer faster and trained solutions to train rescheduling problems. Furthermore, looking at larger disruption contexts will be more ideal for a more realistic contexts as railway transport is becoming a more preferred mode of transport. Furthermore, the designed mathematical model can be used to analyze other performance parameters for instance stability and punctuality of rail operations. In addition, developing a simulation model that considers the main uncertain factors in practical applications and looking at the relationship between train volume and dispatch performance relative to an optimal schedule and its impact on capacity and infrastructure planning can be good research area in the future.

References

1. Wang, Yihui, Andrea D’Ariano, Jiateng Yin, and Lingyun Meng, et al. "Passenger demand oriented train scheduling and rolling stock circulation planning for an urban rail transit line." Transp Res B Methodol 118 (2018): 193-227.

   [Crossref] [Google Scholar]

2. Hong, Xin, Lingyun Meng, Andrea D'Ariano, and Lucas P Veelenturf, et al. "Integrated optimization of capacitated train rescheduling and passenger reassignment under disruptions." Transp Res Part C Emerg Technol 125 (2021): 103025.

   [Crossref] [Google Scholar]

3. Warg, Jennifer. "Effects of increased traffic volume and speed heterogeneity on the capacity of a railway with dense mixed traffic." WIT Trans. Built Environ 127 (2012): 485–497.

   [Crossref] [Google Scholar]

4. Milinkovic, Sanjin, and Sandra Kasalica. "Simulating train dispatching logic with high-level petri nets." TehniCki vjesnik 28 (2021): 639-648.

   [Crossref] [Google Scholar]

5. Shakibayifar, Masoud, Abdorreza Sheikholeslami, Francesco Corman, and Erfan Hassannayebi, et al. "An integrated rescheduling model for minimizing train delays in the case of line blockage." Oper Res 20 (2020): 59-87.

   [Crossref] [Google Scholar]

6. Bettinelli, Andrea, Alberto Santini, and Daniele Vigo. "A real-time conflict solution algorithm for the train rescheduling problem." Transp Res B Methodol 106 (2017): 237-265.

   [Crossref] [Google Scholar]

7. D’Ariano, Andrea, and Marco Pranzo. "An advanced real-time train dispatching system for minimizing the propagation of delays in a dispatching area under severe disturbances." Netw Spat Econ 9 (2009): 63-84.

   [Crossref] [Google Scholar]

8. Corman, Francesco, Andrea D’Ariano, and Ingo A. Hansen. "Disruption handling in large railway networks." WIT Trans Built Environ 114 (2010): 629-640.

   [Crossref] [Google Scholar]

9. Khwanpruk, Somkiat, Kankanit Khwanpruk, Laemthong Laokhongthavorn, and Arkom Suwannatrai, et al. "Optimization-Based Train Timetables Generation with Demand Forecasting for Thailand High Speed Rail System." KSCE J Civ Eng 25 (2021): 3502-3510.

   [Crossref] [Google Scholar]

10. Barbour, William, and Daniel B Work. "Optimization methods for analysis of empirical rail dispatching relative to train plans." J Rail Transp Plan Manag 19 (2021): 100261.

    [Crossref] [Google Scholar]

11. Wang, Yihui, Tao Tang, Bin Ning, and Lingyun Meng, et al. "Integrated optimization of regular train schedule and train circulation plan for urban rail transit lines." Transp Res E Logist Transp Rev 105 (2017): 83-104.

    [Crossref] [Google Scholar]

12. Josyula, Sai Prashanth, Johanna Tornquist Krasemann, and Lars Lundberg. "A parallel algorithm for train rescheduling." Transp Res Part C Emerg Technol 95 (2018): 545-569.

    [Crossref] [Google Scholar]

13. Zhang, Zhengkun, Changfeng Zhu, and Wenhu Ma. "Discrete Optimization on Train Rescheduling on Single-Track Railway: Clustering Hierarchy and Heuristic Search." J Adv Transp 2020 (2020): 19.

    [Crossref] [Google Scholar]

14. Takagi, R, PF Weston, CJ Goodman, and C Bouch, et al. "Optimal train control at a junction in the main line rail network using a new object-oriented signalling system model." WIT Trans Built Environ 88 (2006): 10.

    [Crossref] [Google Scholar]

15. Wang, Yihui, Kangqi Zhao, Andrea D’Ariano, and Ru Niu, et al. "Real-time integrated train rescheduling and rolling stock circulation planning for a metro line under disruptions." Transp Res B Methodol 152 (2021): 87-117.

    [Crossref] [Google Scholar]

16. Gong, Congcong, Jungang Shi, Yanhui Wang, and Housheng Zhou, et al. "Train timetabling with dynamic and random passenger demand: A stochastic optimization method." Transp Res Part C Emerg Technol 123 (2021): 102963.

17. Guo, Yida, Cheng Zhang, Chaoxian Wu, and Shaofeng Lu, et al. "Multiagent System–Based Near-Real-Time Trajectory and Microscopic Timetable Optimization for Rail Transit Network." J Transp Eng Part A Syst 147 (2021): 04020153.

    [Google Scholar]

18. Huang, Kang, Jianjun Wu, Feixiong Liao, and Huijun Sun, et al. "Incorporating multimodal coordination into timetabling optimization of the last trains in an urban railway network." Transp Res Part C Emerg Tec 124 (2021): 102889.

19. Shakibayifar, Masoud, Abdorreza Sheikholeslami, and Francesco Corman. "A simulation-based optimization approach to reschedule train traffic in uncertain conditions during disruptions." Scientia Iranica 25 (2018): 646-662.

    [Google Scholar]

20. Chen, Lei, Felix Schmid, Meena Dasigi, and Clive Roberts, et al. "Real-time train rescheduling in junction areas." Proc Inst Mech Eng J Rail and Rapid Transit 224 (2010): 547-557.

    [Crossref] [Google Scholar]