Proof of the Collatz Conjecture

Hrant A. Gevorgyan^*
*Correspondence: Hrant A. Gevorgyan, Department of Mathematics, Institute of Mechanics of the NAS of Armenia, 24B Baghramyan Ave, Armenia, Email:

Keywords

Even and odd numbers • Even and odd rank • Structure matrix • Contraction mapping

Introduction

L. Collatz formulated his piquant hypothesis in 1932 in an extremely laconic interpretation. Any natural number n is taken. If it is even, then divide it by 2, and if it is odd, then multiply it by 3 and add 1 to the result. Then the same actions are performed on the resulting number, etc. [1]. The Collatz conjecture, or Syracuse problem, is that no matter what initial number n we take, the generated sequence will sooner or later converge to the number 1. This sequence is also called the Syracuse sequence [1,2].

Arithmetic interpretation of the collatz conjecture: It is obvious that the rank of any even number

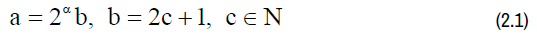
Is precisely determined by the degree of its pairing r_p , namely:

How could one determine the rank of odd numbers? It turns out that if the Collatz conjec-ture is true, then the rank of any odd number would be characterized by the number of transfor-mations carried out according to the Collatz formulas:

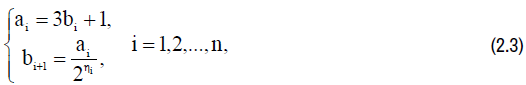
Moreover, the number n would in this case be nothing more than the degree of unpairing of a given odd number, i.e.

In this case, the number 3 turns out to be an odd number of the second rank, and the number 5 is an odd number of the first rank. Thus, it remains to prove the validity of the Collatz conjecture in order to be able to assert the validity of this method of classifying odd numbers. Perhaps, this was the true background to the emergence of the Collatz conjecture.

Reducing the collatz problem to the problem of solving a system of linear algebraic equations: Introducing a certain sequence of odd numbers, we formulate the collatz problem as follows: (Figure 1).

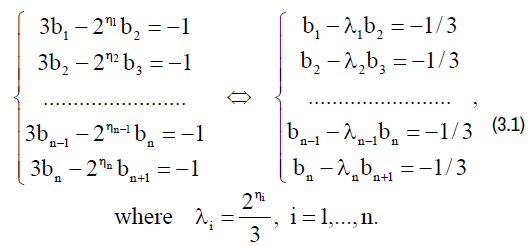
The system of linear algebraic equations (3.1) admits a unique solution provided that in (3.1) b const n 1 = + , based on the analogy with the structural matrix of a simple open kinematic chain H of a multibody dynamic system known in the scientific literature (Figure 1) [3]. In this case we get:

Where from where

The matrix [H]⁻¹ in (3.3), as is known is determined purely analytically. It is expressed through constants λ₁ ,λ₂ ,...,λ_n as follows:

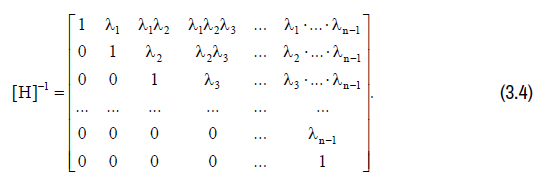
Let us show that in the matrix equation (3.2) 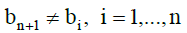. In this case, the Syracuse sequence would enter a closed cycle, and the structural matrix H would take the form:

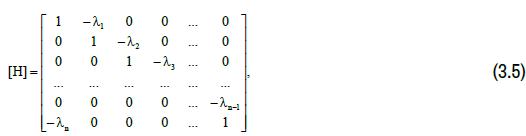
As a result, it ceases to have an analytical expression for the inverse matrix for the variable vector [b] in positive integers. A rigorous proof of the absence of solutions for the system of linear algebraic equations (3.2) involving the matrix (3.5) is achieved using the classical Cholesky scheme (see appendix). In the future it will be shown that in the system of linear algebraic equations (3.2) b_{n+ 1} = 1.

Conditions for the convergence of the Syracuse sequence. Let us consider a sequence that is an original Syracusan sequence (3.1):

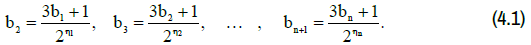
If it were not for the powers of the denominators of the number 2 in the sequence (4.1), then the Syracuse problem could be reduced to the study of some classical sequence of iterations for convergence. So, for example, in the case if η_k = 1 , k = 1,.... ,n , the Syracuse sequence would take the form

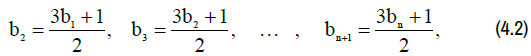
in which it would, generally speaking, be divergent, since the mapping of successive approximations (4.2), namely:

is not contracting because

Let us call sequence (4.2) the limit Syracuse sequence, since the power of 2 in the denominators of the Syracuse sequence takes the smallest value. It is not difficult to verify that none of the original Syracuse sequences actually degenerate to such a sequence. Now recall that in the Collatz conjecture the denominator of the sequence actually varies. Let us show that the denominators of the Syracuse sequence (4.1) with a high degree of accuracy can be assumed to chaotically take one or another power of the number 2. From system (3.1) it follows that

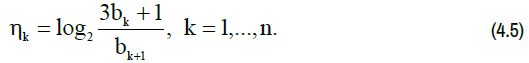
Since the odd numbers b_k and b_k+1 in (4.5), according to another common synonym for the Collatz sequence b₁ ,b₂ ,...,b_n , are the so-called “hailstone numbers”, then the exponents η_k, k = 1,...,n are also quasi-random variables. Therefore, they could be qualified as random variables. We replace the original Syracuse sequence (4.1) with some equivalent sequence in which the exponent of the denominators would take a constant value κ . We will further call the resulting sequence the equivalent Syracuse sequence:

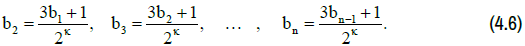
Then it would be easy to notice that for κ > κ* =1.6 the mapping of the sequence (4.6)

would be contracting, since

To achieve complete equivalence between sequences (4.1) and (4.6), it is necessary to establish an exact value κ in (4.6), which is an indefinite function of exponents η_k, k =1,...,n , i.e.

The exact expression for the value κ , if it exists, is impossible to indicate due to the lack of a specific analogue for dependence (4.9), which establishes a connection between sequences (4.1) and (4.6). However, regarding the abstract dependence (4.9), it can be stated with all rigor that the value κ directly depends on all exponents η_k, k = 1,...,n . Moreover, assuming the truth of the Collatz conjecture, one could also argue that for any original Syracusan sequence (4.1), the equivalence exponent in (4.6) must be κ > κ* =1.6 on the grounds that every Syracusan sequence is convergent.

It is not difficult to guess that the above-mentioned property of the abstract dependence (4.9) between the exponents of the original (4.1) and equivalent (4.6) Syracuse dependences includes well-known expressions for the arithmetic mean and the geometric mean. So, for example, in the case of identifying the equivalence exponent κ of the sequence (4.6) with the value of the arithmetic mean of the exponents of the sequence (4.1), we obtain the following approximation for the exponent κ : (Figure 2).

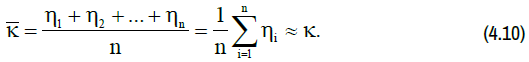
If the true equivalence exponent is replaced by its approximation (4.10), the equivalent Syracuse sequence (4.6) would be rightfully called a simplified Syracuse sequence, which would look like this:

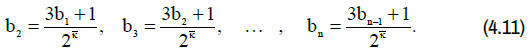
At the same time, it should be noted that in the simplified Syracuse sequence (4.11), in contrast to the equivalent Syracuse sequence (4.6), the approximate equivalence exponent 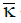can also take on the values 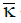< κ* =1.6 .

Justification for the convergence of the Syracuse sequence: Let us present a justifica¬tion for the fact that the exponent in the equivalent Syracuse sequence (4.6) increases monoto¬nically with increasing field of variation of numbers. It is well known that as numbers increase, the distribution density of prime numbers decreases monotonically; it is not difficult to verify that the density of even numbers of the first rank remains unchanged everywhere, amounting to exactly 50% of the total number of even numbers, since we are talking about the asymptotic den-sity of numbers of the form. At the same time, with an increase in the field of change of numbers, more and more even numbers of the second and higher ranks appear, and also there is a gradual appearance of numbers of higher and higher degrees of pairing. Then, as the scatter field of numbers of the Syracuse sequence grows, we will have a table of the distribu-tion of the entire range of powers shown in Figure 2, therefore, due to the assumption of the ran-dom nature of the choice of power exponents in (4.9), the exact value will continuously in-crease (Figure 2).

From the above it follows that as the field of scatter of numbers grows, the exponent κ in the equivalent sequence (4.6) invariably increases, reaching somewhere and then exceeding the critical value κ* =1.6 . There is also a continuous increase in the simplified exponent κ in (4.11). This means that the Syracuse sequence cannot be divergent. In other words, we are dealing with a sequence of variable convergence, or contractibility, monotonically increasing as the field of number scatter increases. This circumstance explains the fact that large numbers converge to one “faster” than some two-digit numbers, which, like hailstones, meander for a long time before “shrinking” to one. This is where the figurative expression “hailstone numbers” came from due to the fact that the graphs of the Syracuse sequence are similar to the trajectories of hailstones in the atmosphere. So, in Figure 3 shows a graph of the convergence of the number 27, which, due to the recognition of the Collatz conjecture as a theorem, could be qualified as an odd number of rank 41.

Now it remains to pay attention to the statement in paragraph 2 that b_n+1 = 1 . Currently, through ordinary computer recalculation, it has been shown [2] that all positive integers up to the number 9.10²¹ (nine sextillion) and higher obey the Collatz conjecture. For such large values, the exponent κ significantly exceeds the critical value κ* =1.6 , which means that for numbers b_i > 9.10²¹. there is a guaranteed contraction of the Syracuse sequence. Consequently, any initially taken odd number, after a certain finite number of iterations, must sooner or later “squeeze” to unity. The only number among all natural numbers, one, which maps onto itself, can be conventionally called a nodal number, or an odd number of 0-rank (Figure 3).

Conclusion

This article presents a proof of the world-famous Collatz conjecture. The use of a special structural matrix from the theory of multibody dynamic systems made it possible to significantly simplify the mathematical justification for the existence and uniqueness of a solution to the Syracuse problem, provided that the obvious requirements are met. The Syracuse sequence has also been studied for classical convergence, from which follows the property of its guaranteed contraction for large numbers.

Appendix

Let us show that the system of linear algebraic equations (3.2) in the context with matrix (3.5) is not resolved in positive integer numbers of variables b_i , i = 1,...,n .

Let us use the Cholesky scheme to invert matrix (3.5). Then matrix equation (3.2) is written as:

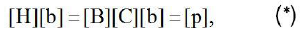
For simplicity, in the system of linear algebraic equations we will assume: n = 4 . Therefore, for a matrix [H] of size (4x4) :

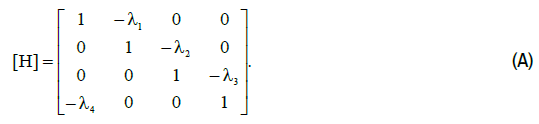
The matrices [B] and [C] take the form

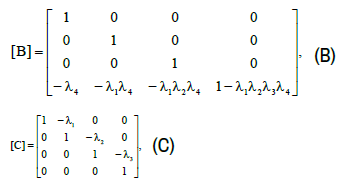
From where the matrices [C]⁻¹ and [B]⁻¹ will accordingly have the form

From the last equation of the system, taking into account the fact that the column vector [p] in (3.2) no longer contains the product λ_n b_n+1 , the expression for the last component of the needed column vector [p] follows:

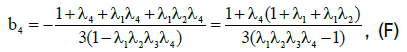
Expressing in the last form of recording an irreducible fraction containing the parameters: λ₁ ,λ₂ ,λ₃ ,λ₄ . It is easy to conclude that if we were talking about a system of linear algebraic equations of dimension n, then the similar component b_n in (F) would in this case contain the variables λ₁ ,λ₂ ,...,λ_n . However, the last variable b_n of the Collatz sequence , by definition, cannot depend on all parameters λ₁ ,λ₂ ,...,λ_n , since it is a function of only the parameter λ_n . It follows from this that the matrix [H]⁻¹ inverse to the matrix [H] in the form (A) does not allow the system of linear algebraic equations (3.2) to be resolved in positive integers (natural numbers). It is easy to see that this is possible only when the composite matrix of the Cholesky scheme [B] = [B]⁻¹ = [I], where is the identity matrix. What needed to be demonstrated.

References

1. Hayes, Brian. "On the ups and downs of hailstone numbers."Scientific American 250 (1984): 10-13.

   Google Scholar

2. Stewart, Ian. “The great mathematical problems.” Profile Books, (2013).

   Google Scholar

3. Gevorkian, H. A. "Simulation of elastic tree-like dynamic systems in presence of external holonomic constraints."Herald of the Bauman Moscow State Technical University. Series Natural Sciences2 (2020): 4-24.

   Google Scholar