Research Article - (2022) Volume 9, Issue 9
Received: 19-Aug-2022, Manuscript No. jlop-22-72423;
Editor assigned: 20-Aug-2022, Pre QC No. P-72423;
Reviewed: 31-Aug-2022, QC No. Q-72423;
Revised: 05-Sep-2022, Manuscript No. R-72423;
Published:
12-Sep-2022
, DOI: 10.37421/2469-410X.2022.9.41
Citation: Monks, James N and Zengbo Wang. “PT Symmetry
Breaking for Ultraviolet Switchable Lasing to Anti-lasing States.” J Laser Opt
Photonics 9 (2022): 41.
Copyright: © 2022 Monks JN, et al. This is an open-access article distributed
under the terms of the Creative Commons Attribution License, which permits
unrestricted use, distribution, and reproduction in any medium, provided the
original author and source are credited.
Sources of funding : The authors acknowledge the financial support part-funded by the European Regional Development Fund through the Welsh Government (BU262).
The investigation of symmetries inspired by quantum mechanics in optical and photonic systems has generated a great deal of fundamental and technological research. Non-Hermitian physics based on parity-time (PT) symmetry, which was first postulated in research related to quantum mechanics and quantum field theory, is one of the key emerging subjects. The intriguing physical effects made possible by non-Hermitian physics have greatly expended the possibilities for engineering new materials, applications, and technologies. This research reports on a two-dimensional nanoparticle system that can switch between a lasing and anti-lasing state when the PT symmetry is broken. The nanoparticle system consists of a loss-gain balance with silver nanoparticles and a conjectural material derived from the complex conjugate of the permittivity of silver in accordance with PT symmetry conditions. The eigenvalues bifurcation demonstrates that the system is non-Hermitian when symmetry is broken. This research offers the foundations for compact system with applications in many fields where lasers and anti-lasers are required including targeted radiological medicine.
PT symmetry • Symmetry breaking • Mie theory • Plasmonics • Quantum mechanics
Lasers are a tool that have revolutionised our world and have found applications in all sections [1] from microbiology to nuclear fusion. In 1917, Einstein laid the foundations for the laser by explaining how light is made up of photons which led to the theoretical description of stimulated emission [2]. From these principles, a team at Yale university led by theorist Douglas Stone observed the Feynman diagrams for lasers and noticed that if the time were reversed, an opposite effect could take place where the light is perfectly absorbed at a single wavelength [3]. This process is known as a coherent perfect absorber (CPAs) or anti-lasers. The collective behaviour of absorbing particles can be described through Mie’s theory [4].
Most processes in the universe are time reversal, which means that they work irrespective of the direction of time, with the exception to entropy. Parity (P) or spatial symmetry implies that the laws of physics are indifferent to left or right handedness. In the 1950s it was thought that all fundamental particles conform to parity, time-reversal (T) and charge symmetry (C). In 1956, Lee and Yang published their findings discussing that P-symmetry within the weak force had never been experimentally tested [5]. The following year, Chien-Shiung Wu and her team conducted an experiment confirming that P-symmetry could be broken [6]. This led to Lee and Yang winning the 1957 Nobel Prize in physics for their contributions to parity law [7]. It was later discovered by Cronin and Fitch that time-reversal symmetry can also be broken [8], of which the pair won the 1980 Nobel Prize in physics. This led to parity and time-reversal being excluded from the geometrical symmetry of nature. Although CPT symmetry remains a geometrical symmetry of nature; more recent research is testing the validity of CPT symmetry by studying the cooling of antihydrogen [9]. If a difference were to emerge, it could change and impact every cornerstone of modern physics.
Energy plays a vital role in physics. It provides a quantifiable measurement for a given system in terms of a real number. However, in order to obtain this value, it is assumed that the energy must be Hermitian. In 1998, Bender and Boettcher put forward the notion of space-time reflection (Parity-Time) symmetry, which is defined as a complex generalisation of conventional quantum theory [10]. This theory enabled non-Hermitian Hamiltonians to exist with a real spectrum providing that the PT symmetry remained unbroken. The presence of broken symmetry would also result in complex eigenvalues. This was initial thought to be only an interesting mathematical discovery with little expectation for practical applications. Over the last decade, the topic has been extensively explored in the world of optics and photonic research [11-13], both theoretically and experimentally. The emergence of PT symmetry within optics has led to the experimental exploration in the areas of optical waveguides [14], lasers [15], resonators [16], and metamaterials [17].
In this paper, we show that a PT-symmetric system, consisting of a coupled two-dimensional nanoparticle array with balanced gain and loss, offers a promising platform for a switchable laser to anti-laser system when the symmetry is broken. Under PT-symmetry, the system remains at equilibrium with only a natural resonance existing. Once the parity symmetry is broken, depending on the direction, the balanced gain to loss particles become unbalanced which enables switching of activities between gain and loss functions. Sensitivity enhancement on the perturbation strength and gain, or loss, is dependent on the spatial distance between particles. The research provides potential applications in interferometry, radiology, astronomy, defensive countermeasures, signal detection, and much more.
Theory
In 1998, Bender and Boettcher presented their findings which demonstrated that quantum systems with a non-Hermitian Hamiltonian can have a set of eigenstates with real eigenvalues that corresponds to a real spectrum [10]. They noticed that the Hermiticity of the Hamiltonian is not a required circumstance for obtaining real eigenvalues. Thus, new quantum mechanics can be established by such Hamiltonians. PT symmetric quantum mechanics is an action of extending quantum mechanics into the complex domain, and if PT symmetry is a respected principle, the eigenvalues can remain real and unitarity can be preserved even if the Hamiltonian is not Hermitian.
An example of a PT symmetric Hamiltonian is provided below and is obviously not Hermitian due to the extension into the complex domain. This simple example remains under a PT symmetric Hamiltonian since under parity,x changes sign and under time-reversal, i changes sign.
Where;
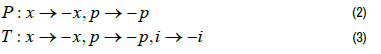
This simple cubic Hamiltonian has been studied by numerous researchers, most notably in the one-dimensional model of Lee-Yang edge singularity [18] and Reggeon field theory [19] and is one parameter family of PT-symmetric Hamiltonians obtained by a complex deformation of the harmonic oscillator.
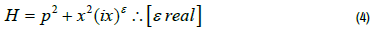
Where ε is the complex deformation character (Figure 1).
The plot presented in Figure 1, demonstrates the real eigenvalues for a PT-symmetric Hamiltonian. The region of unbroken PT symmetry is ε≥0. In the region of broken symmetry, εε<0, the eigenvalues emerge from the complex plane at exceptional points as degenerate pairs that split into real eigenvalues. As ε approaches the critical point of zero, the de-complexification process begins with low-lying eigenvalues that terminates at ε=0 during the highestlying eigenvalues.
The quantum mechanical PT symmetry concepts can be extended to the optical domain and can be introduced, in a two-dimensional case, by reducing Maxwell’s equations to the scalar Helmholtz equation.
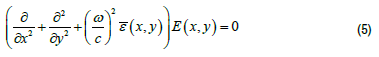
This corresponds with the stationary Schrödinger equation.
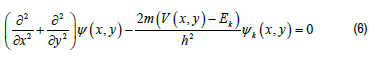
The formal substitutions V(x,y ) - E k →(ω/c )2ε (x , y) ψk (x , y) → E( x , y )and h2 (2m)→1. The PT symmetry condition reduces to the constraint V (x, y) =V* (−x,− y) executed on the potential energy. Consequently, the correlation between the potential energy in quantum mechanics and the permittivity in optics, the PT symmetric condition for an optical system is defined as the condition inflicted on the permittivity (ε )of the given medium.
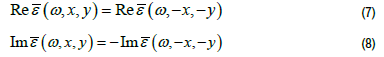
The stationary Schrödinger equation does not include the time dependency, thus, the time reversal operation, T-symmetry, is equivalent to the K-vector symmetry, which continues to satisfy the conditions of an optical PT-symmetric system [20].
Loss-Gain Medium
Gonzalo Muga introduced PT-symmetry into the field of optics and noted that PT-symmetry corresponds to the presence of balanced gain and loss [20]. A lossy material is defined as one that dissipates electromagnetic energy passing through it. Absorption is often the main driver behind lossy materials and is actioned by how the bound electrons take up photon energy and transform that electromagnetic energy into internal energy of the absorber. On the other hand, gain materials enable the process of energy transfer to emit electromagnetic radiation, resulting in increased optical power. The main component to describe lossy and gain materials is associated to with the imaginary part of the permittivity.
The lossy material used in this system is silver in the form of spherical nanoparticles. The refractive index data has been collected from Johnson and Christy [21] and converted into the permittivity, (Figure 2). A spherical nanoparticle has been selected to take advantage of the localised surface plasmon resonance, which results from irradiating light with an oscillating electric field, interacting with the conduction electronic in the silver and allows them to coherently oscillate. This enhances the electric fields near the particle’s surface and improves the particle’s optical absorption properties. The permittivity of the conjectural gain medium has been formulated by the complex conjugate permittivity of the lossy component, (Figure 2).
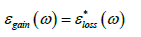
The complex conjugate for the gain material facilitates the imaginary part in ε*loss (ω ) loss ε ω to change its sign but in doing so, the Cauchy-Riemann conditions are no longer satisfied. This can result in singularities and a non-causal function; however, the systems PT-symmetry conditions remains satisfied for discrete frequency sets (Figure 2a).
The loss and gain mediums are situated in air. As such, the permittivity of both materials will form a Lorentzian dispersion that can be calculated from the Maxwell-Garnett theory.
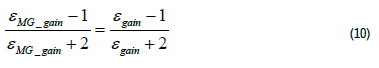
Where f is the volume fraction, εMG − gain is the Lorentzian permittivity for the gain medium, and εgain is the permittivity of the gain medium. For εMG_Loss , the εgain can be replaced with εloss (Figure 2b). The Lorentzian permittivity fulfils the PT symmetric conditions for an optical system as previously discussed in equations (7) and (8).
Mie theory can be used to observe the natural resonances produced from the plasmonic interactions. Mie theory formulates the relation of lightmatter interactions and outlines a systematic solution for the light lost by small spherical particles through Maxwell’s electromagnetic theory. The solutions show that the electric and magnetic fields are present inside and outside a homogeneous spherical particle. The theory is formulated by expressing a plane wave in terms of spherical harmonics and calculating the field that overlap the spherical harmonic modes supported by the particle. It is an exact analytical description of the electrodynamic response of a particle, described by the total extinction cross-section efficiency, the summation of absorption and scattering.
Figure 1. Real eigenvalues of the PT-symmteric Hamiltonian plotted as a function of ε
Figure 2. (a) Real and (b) imaginary parts of the permittivity for an absorbing (red solid curve) and gain (blue dashed curve) media in the case where the imaginary pats differ only in sign: Im(εloss )= − Im( εgain)
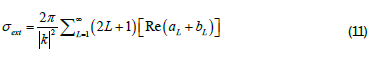
Where k is the wave vector and L are integers representing the dipole, quadrupole, and higher multipole of the cross-sections. a L And bL are parameters that are composed of Bessel functions Ï?L and X L .
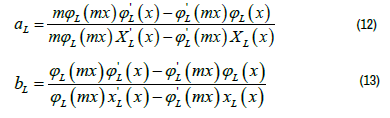
Where m = ñ/nd , with ñ denoting the complex refractive index of the lossy nanoparticle, and d n indicating the refractive index of the non-absorbing surrounding medium. Additionally, x = k m a , where a is the radius of the particle and km is the wavenumber in the medium.
If the nanoparticle is assumed to be much smaller than the incident wavelength α<<γ, then the Bessel functions can be approximated by the power series in accordance to Bohren and Huffman [22], where the terms are to order x3 , allowing the aL and bL parameters to simply to the following, with the higher order terms of aL and bL equalling zero (Figure 3).
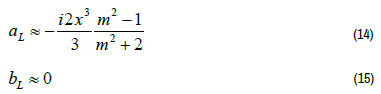
Mie theory and PT symmetric quantum theory provide the base analytical principles for this research. The use of full-wave numerical simulation software (CST Microwave Studios) has been used to solve the far field responses. The light propagation direction, K-vector, with normal incidence is perpendicular to the design surface. The electric field is directional to the y-axis and the magnetic field is directional to the x-axis.
The optical system for this study consists of an arrangement of interchanging loss and gain nanoparticles, along the y-axis, situated in free space (Figure 4). The system conforms to a PT symmetric optical system due to the Lorentzian permittivity’s of the loss and gain mediums as set out in equations (7) and (8). However, the balance between the loss and gain becomes broken when the parity deviates from 35 y Δδ = nm . Parity along the x- and -z-axis remains at equilibrium. This parity change simultaneously breaks the permittivity symmetries, resulting in an unbalanced loss and gain system that leads to instantaneous Time-reversal symmetry breaking.
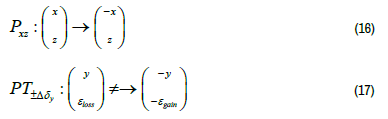
In other words, by positively or negatively adjusting y Δδ , the states switch from physical equilibrium (a state of unbroken PT symmetry) to nonequilibrium (a state of broken PT symmetry), and in doing so, the particle behaviours switch activities. Note that y Δδ occurs at interval spaces between the arrays to force an unsymmetric parity (Figure 4).
Figure 3. The Lorentzian permittivity dispersion for the loss and gain materials in accordance with the Maxwell-Garnett theory.
Figure 4. The cross-section extinction efficiency for the loss and gain nanoparticles with a radius of 20 nm.
The transmission spectrum presented in Figure 5 demonstrates the far field optical responses of the two-dimensional system during the unbroken and broken states of symmetry. The natural resonance of the particle arrangement presents broadband trough at ~360 nm wavelength, as demonstrated by the analytical cross-section extinction calculations. Under directional parity breaking, the transmission spectrum can selectively switch from optical gain to perfectly absorbing at a narrowband region at ~350 nm wavelength. The optical gain is revealed by the > 1transmission amplitude (Figure 5).
A more in-depth analysis of the selective directional tuning can be found in Figure 6 which presents a contour plot for the transmission range as a function Δδ with respect to the wavelength. The plot demonstrates that as the δγ function increases spatially, a narrowband optical gain (lasing) state arises. Opposingly, as the δγ function decreases spatially, the narrowband absorptions formed from PT symmetry break approaches a perfect coherent absorbing (anti-lasing) state. Additionally, the resonant state becomes more broadband with increased transmission attenuation with the spatial tightening along the y-direction which matches the Mie theory description (Figure 6).
The near field interactions, Figure 7, shows the electromagnetic field behaviour in decibels within the described system. At equilibrium (Figure 7a), the EM field is distributed within a fishnet formation that is equally coupled throughout and is represented through the symmetry of the EM field isoline distribution pattern. When the system is presented with a negatively broken symmetry along the y-axis, the loss material interacts with the EM fields in a dipole fashion with the loss and gain nanoparticles becoming strongly coupled. Any optical gain is lost within the absorbing lossy nanoparticle and result in a perfect coherent absorber. When the system is presented with a positively broken symmetry along the y-axis, the gain particle becomes highly excited resulting in increased optical gain and improved lasing efficiency (Figure 7).
Figure 8 shows the key principles of PT symmetry by observing the eigenvalues that present as non-Hermitian, complex notion. The behaviour of the eigenvalues of the PT symmetric system highlights the bifurcation associated with the symmetry breakdown. In literature, the discussion on complex Hamiltonians is built on dynamical systems that evolve in time and space through linear operators. However, the system which this paper presents, like many PT photonic systems, is open and coupled to a continuum of radiation modes by finite-sized nanoparticles illuminated by impinging optical fields. As such, the eigenvalues presented here are described through
Figure 5. The schematic diagram of the loss-gain two-dimensional arrayed particle system, with the K-vector propagating along the z-axis.
Figure 6. Transmission spectrum of the two-dimensional loss-gain particle array, expressing the broken and unbroken states for the case of ± Δδ = 16nm .
Figure 7. Range of transmission as a function of Δδ with respect to wavelength. The contour plot highlights the areas of broken symmetry in the forms of lasing and antilasing states.
Figure 8. The near-field interactions at 350 nm wavelength of the loss-gain particle array for the situations of (a) unbroken symmetry, (b) negatively broken symmetry, and (c) positively broken symmetry. The isolines indicate the interaction and coupling strengths.
Figure 9. The modulus of the S matrix eigenvalues plotted against the particle size parameter [a] verse wavelength[λ ] .
the S-matrix, which directly relates incoming waves and outgoing waves. The S-matrix is evaluated with the time-evolution operation, e−iHξ in a Hamiltonian system. The S-matrix without the loss and gain material is unitary and remain Hermitian. With the presents of the loss and gain material the corresponding eigenvalues reveal a transition from purely real (exact PT symmetry – equilibrium state) to complex notation (broken PT symmetry – non-equilibrium states) (Figure 9).
A system of loss-gain nanoparticles with non-Hermitian properties that can switch from a lasing to anti-lasing state has been presented. The optical gain and narrowband perfect absorption occur at ~350 nm within the UV region. The gain material has been derived from the complex conjugate permittivity of silver and could be realised by doping a material with rare-earth ions and transition metal ions. When symmetry within the 2D system is unbroken, the system remains in a stable state, allowing for an ON-OFF state to exist with the ON state either under lasing conditions or anti-lasing conditions depending on the direction of symmetry breaking. The presented research hopes to offer the foundations for new technologies to exist that scales across a broad number of applications with the advent of new and efficient nano-fabrication technologies to support the manufacturing.
The authors acknowledge the financial support part-funded by the European Regional Development Fund through the Welsh Government (BU262).
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Journal of Lasers, Optics & Photonics received 279 citations as per Google Scholar report
