Review Article - (2020) Volume 9, Issue 2
Received: 11-May-2020
Published:
29-May-2020
, DOI: 10.37421/idse.2020.9.244
Copyright: © 2020 Abdusamadovich SU. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which
permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
The article considers the flow efficiency and operational reliability of large canals. In order to raise efficiency and reliability of exploitation of canals hydraulic control model to change the flow depth was created. It was determined by the law of water transmission in optional time. Patterns based on determination of hydraulic relations under changing values of hydraulic parameters of water flow in the trapezoid cross-section irrigation canal were examined.
Large channel hydraulic model speed • Flow rate • Water depth • Reliability • Flow efficiency
The lifetime of our channels of from 30 to 55 years, many of them are characterized by a degraded technical condition, and consequently, reduced hydraulic efficiency and operational reliability. This is due to several factors: the deformation of the beds of the channels, erosion and sedimentation, destruction of the wall and joints, increased roughness of their channels, the overgrowing of the bottom and slope of water races- Titulescu, considerable losses of water through seepage, the change of regime and conditions. The influence of these factors leads to decrease in throughput (sometimes several times) of the channel, the deviation of the main parameters of the living section of the channel (depth, width) from the design values, increased losses of water through seepage, significant reduction in the efficiency of the channels, failures in their work, namely, to dam breaks, destruction of plates, clothes, flooding, flooding adjacent to the channel areas.
Under the hydraulic effectiveness of the major channels to understand the provision of high bandwidth to their channels in the process of operation close to the design with minimal loss of water, not exceeding the permissible values. Under the operational reliability of the irrigation channels as providing a reliable and safe operation in compliance with the required efficiency during the service life [1,2].
However, the problems of hydraulic efficiency and the operational reliability is still not fully resolved due to the variety of influencing factors and the complexity of the processes leading canals to various deformations, growth, siltation and failure.
Issues the hydraulic efficiency and the operational reliability of the major channels in the country and abroad are considered in detail. In many studies it is shown that the main criteria of hydraulic efficiency and operational reliability of irrigation canals can serve the following conditions [3-5]:
whereÕ -function of efficiency and reliability related indicators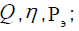 
and
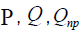- actual and estimated throughput; 
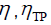- the actual and the desired efficiency of the channel; 
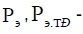the actual and the desired indicators of the technical state of the rope; 
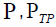- the actual and the desired probability of failure-free operation;
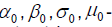coefficients valid reduction of the relevant normative parameters taken according to the results of statistical processing of field data.
However, to ensure reliability of the design and effective operation of large channels require the study of patterns to establish hydraulic dependencies when changing the values of hydraulic parameters of water flow.
For example, the movement of water in the channel is one-dimensional, and the density, viscosity and velocity of sediments water are constants. Using the above condition, we will install a hydraulic model to control the depth of the water flow.
Hydraulic driven model of changes in the average velocity of water flow in irrigation channels, due to the exponential regime of water supply [6-10].
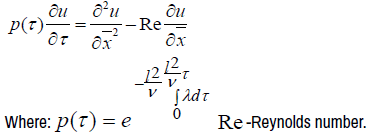(1)
For the solution of equation (1) will enter the function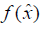 
in the form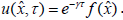 
Given this equality, the equation (1) will be as follows:
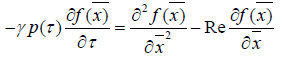(2)
The function will write as
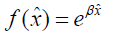(3)
Then from (2) to β get the characteristic equation
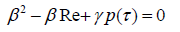(4)
Solving equation (4), we get
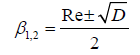
where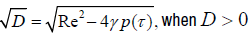 
Then the solution to the above equations will be
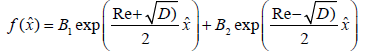(5)
Using the methods of Kramer given the conditions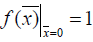 
, 
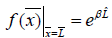, determine the unknown coefficients of equation (5):
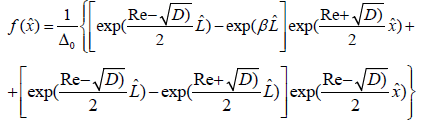(6)
Thus, the obtained one-dimensional pattern of changes of velocity of water flow in the larger channels due to the exponential flow of water to an arbitrary point in time [11-15]:
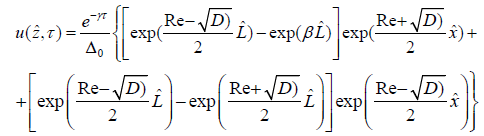(7)
According to the decision of tasks will determine the depth of flow of water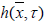 
using equation (7) for a compliant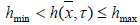
Suppose that u ≈V , in this case, equation (7) takes the form:
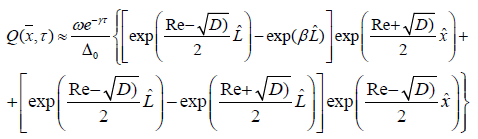(8)
Considering (8) we obtain the equation controlling depth of flow under varying values of hydraulic parameters of water flow of water in an irrigation channel in the form of trapezoidal cross-section [16-19] (Figure 1):
Figure 1. Siltation of bottom of the riverbed irrigation canal.
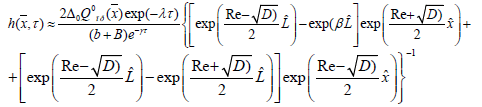(9)
To improve the reliability of effective operation of major channels received hydraulic management model to change the depth of water flow in the major channels is caused by the exponential law of water flow for an arbitrary point in time.
Irrigation & Drainage Systems Engineering received 835 citations as per Google Scholar report
