Scientific Substantiation of the Method for of Low- Optimization Intensity Irrigation Systems With Micro Device

Rae ZH Aliyev^*
*Correspondence: Rae ZH Aliyev, Institute of Soil Science and Agro chemistry of NAS of Azerbaijan, Azerbaijan, Tel: 994125383567, Email:

Introduction

In order to achieve a serious innovative breakthrough in the field of agriculture and agriculture in Azerbaijan, there is a need to fully clarify the existing problems.

Studies show that the following problems are particularly serious:

- Increase of ecological changes, natural cataclysms, anthropogenic impact on agro ecosystems, increase of erosion processes in soils, increase of soreness and insemination,

- Negative orientation of modern fundamental and applied research to the strategic solution to existing problems in agrarian sphere,

- Climate, soil, water, etc. efficient use of resources and their protection, etc. the urgent solution of many problems is the demand of the day. It is also of exceptional importance to optimize the management of irrigation in the current state of the water shortage in the country, and its rebuilding on the basis of modern technology is a major challenge to be solved as important research trends [1,2].

The Course of the Research

When applying the method of dynamic programming solution to the problem of resource allocation leads to address the functional equation under given constraints Bellman view equalities or inequalities:

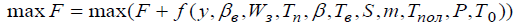           (1)

Q≤Q_max

(K) (T) ≤ K₀

WhereF is maximized functional, in General, income from crop;

(T)-the quality of the harvest;

To₀ -border quality;

Q -irrigation norm;

Q_max-maximum irrigation norm;

f -function of vegetation.

Bellman principle [3,4] means that regardless of the status of the control object at time t the remaining resources should be spent in an optimal way. Adopted the hypothesis of nevosstanavlivae to yield losses due to lack of moisture. When applying dynamic programming treatment is relatively easy: the limitations it provides to the usual tasks of mathematical programming.

When solving particular tasks with dependencies (f) free-form decision usually starts at the end of the specified time interval. While we have a solution on the t step in the solution's features on t-1 step and is remembered as the tabulated function of maximum functionality depending on the balance of resources [1,3]. Then the process continues on t-step 2, etc

When this padding becomes a function of the unknown resource values in the table, and after reaching the beginning of t= 0 when the initial resource, there is a set of joined tables, by which produced straight stroke method: starting with the first step with the building rooms step; because at each step there is a resource used and optimal in this resource before t behavior when transitioning between tables.

Dynamic programming method also allows you to solve problems with the conditions of the cross-cutting approach, i.e. with undocked right end with lack of ill harvest time fastening and time phase transitions of plants. [3,4]. in the application of calculus in the presence of the equation (5.54) for any object is usually solved the problem of optimization of integrated functionality:

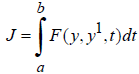          (2)

Which is reduced to the solution of the Euler equations

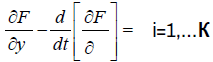           (3)

Where J is maximized functionality. If there are restrictions of the type equations on integrals can be done using the method of Lagrange multipliers, a task with a constraint on total water consumption for irrigation.

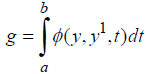            (4)

then the Euler equations becomes:

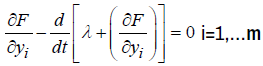           (5)

where λ is the Lagrangian multiplier; m is the number of constraints.

With the limitations of the form:

λ-Lagrange multiplier is replaced by Lagrange function λ (t) and the equations of the form:

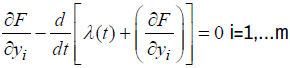           (6)

When limitations common type inequalities the valueof iis done quite difficult, because one has to resort to non-linear change of the conditions, something that makes it very difficult primary challenge.

A kind of variation is the task of Atask and Bolza. the terms ' that add additional terms into the system through a floating right side-lack of fixing the time of harvest and times change vegetative phases [2,4].

When you use the maximum principle for finding the extremum of the integral functional (F) needed to be addressed in a major (5.55) and flip (5.58) systems of differential equations, minimizing the Hamiltonian h:

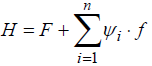             (7)

Where ψ_iis the solution of the coupled system and ψ₀=F optimality criterion

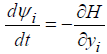           (8)

Under the terms of the task_i (0) = C_(i).

In General, the task is a peer-to-peer with boundary conditions it must be satisfying conditions at two points.

In the systems of differential equations increases twice, because faced with the primary and associated tasks. However, dealing with the limitations of both types of equations and inequalities, type here is relatively easier than in variation calculus.

Task variation in any of the mentioned options can be resolved on the basis of the knowledge base by using artificial intelligence expert systems assessments. It is helpful to apply hybrid systems, partly using conventional methods of optimization and modeling. The use of artificial intelligence in the form of the hybrid system allows you to replace, to a large extent, the task of identifying knowledge gained in the process of research and industrialeconomic activities.

Thus, proceeding from the complexities of working with constraints, it is necessary to abandon the use of calculus.

It is clear that despite the need for double passage, dynamic programming is quite acceptable for the problem of optimization of crop irrigation regime. In addition to these, there are common techniques enough private methods adapt to optimize the moisture of crops, such as based on the theory of statistical decisions matrix constructed taking losses. [74,208,210 etc].

In the work of the task of selecting the irrigation regime on the basis of climate, regulatory and statistical models for rainfall forecast, taking into account forecasting accuracy is accepted one of three strategies:

S_CL -climatic,

S_n -normative (based on established standards),

S_p -forecast (based on statistical data processing and of methods of regression analysis),

S_opt -optimal.

Task definition S_CL, S_h, S_p are resolved in the context of the plan for the year based on years of historical data on crop yields, precipitation, solar radiation, etc. in the same place problem operational management of irrigation, solvable in terms of months. It did not, however, examines the current state of the plants, the forecast weather conditions, soil moisture and the effect of fertilizing.

To address the operational challenges are encouraged to use the method of dynamic programming.

Thus, the most natural and practical way to solve the tasks of optimization of irrigation regime is dynamic programming method adapted to the respective conditions of agriculture.

References

1. Aliev, Jafarov. “Use of the metod of the Dynamic Programming in process of optimization of the irrigation agroculture in condition of mountain agroculture.” The Ninth International Congress Of Baku (2007).
2. International Center A/C Research in the dry in the Dry Areas (ICARDA).“Irrigation regime and monitoring equipment.” Umarova and a. Karimov Taraz: IC AQUA (2002): 128.
3. Us Nosenko Irrigation in the mountains.“Publishing House Kolos Moscow” (1981):143.
4. Zakir Aliev.“Question To protect soil in Azerbaijan republic husbandries/Journal of water and land development, the Institute for Land Reclamation and Environmental Engineering in Agriculture.” Polish academy of Sciences (2005): 116-121