Research - (2020) Volume 14, Issue 2
Received: 25-May-2020
Published:
18-Jun-2020
, DOI: 10.37421/1736-4337.2020.14.299
Citation: Manelo, Anona. “Semi-Simplicity of a Lie Algebra
of Isometries.” J Generalized Lie Theory Appl 14 (2020): 299. doi: 10.37421/
GLTA.2020.14.299
Copyright: © 2020 Manelo A. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
A spray S on the tangent bundle TM with a n dimensional differentiable manifold M defines an almost product structure Γ (Γ2 =I, I being the identity vector 1-form) and decomposes the TTM space into a direct sum of horizontal space (corresponding to the eigenvalue +1) and vertical space (for the eigenvalue -1). The Lie algebra of projectable vector fields  whose Lie derivative vanishes the spray S is of dimension at most n2 +n. The elements of the algebra
whose Lie derivative vanishes the spray S is of dimension at most n2 +n. The elements of the algebra  belonging to the horizontal nullity space of Nijenhuis tensor of Γ form a commutative ideal of
belonging to the horizontal nullity space of Nijenhuis tensor of Γ form a commutative ideal of  . They are not the only ones for any spray S. If S is the canonical spray of a Riemannian manifold, the symplectic scalar 2-form Ω which is the generator of the spray S defines a Riemannian metric g upon the bundle vertical space of TM. The Lie algebra of infinitesimal isometries which is written
. They are not the only ones for any spray S. If S is the canonical spray of a Riemannian manifold, the symplectic scalar 2-form Ω which is the generator of the spray S defines a Riemannian metric g upon the bundle vertical space of TM. The Lie algebra of infinitesimal isometries which is written 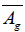 contained in
contained in  is of dimension at most
is of dimension at most 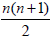 . The commutative ideal of
. The commutative ideal of  is also that of
is also that of 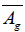 . The Lie algebra
. The Lie algebra 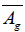 of dimension superior or equal to three is semi-simple if and only if the nullity horizontal space of the Γ Nijenhuis tensor is reduced to zero. In this case, Ag is identical to
of dimension superior or equal to three is semi-simple if and only if the nullity horizontal space of the Γ Nijenhuis tensor is reduced to zero. In this case, Ag is identical to  . Mathematics Subject Classification (2010) 53XX • 17B66 • 53C08 • 53B05ns.
. Mathematics Subject Classification (2010) 53XX • 17B66 • 53C08 • 53B05ns.
Differentiable manifolds • Lie algebra • Spray • Nijenhuis tensor Riemannian manifolds • Infinitesimal isometry
Frölicher-Nijenhuis and Rund H.’s works [1,2] have enabled Grifone J. [3,4]) to show a connection as a vector 1-form Γ such that JΓ=J and ΓJ=-J of which J is the natural tangent structure of the tangent bundle TM to a differentiable manifold M. Such Γ is an almost product structure (Γ2=I), I being the identity vector 1-form. This formalism allows a more algebraic approach for the study of Lie algebras defined by Γ [5].
Given a paracompact differentiable manifold M of n ≥ 2 dimension of class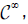 Γ is a connection [3]. In [5], we studied the associated Lie
algebras to Γ, through their first Chevalley-Eilenberg cohomology spaces,
namely, the Lie algebra of vector fields AΓ on TM, whose Lie derivative
applied to Γ is zero, and the horizontal nullity space
Γ is a connection [3]. In [5], we studied the associated Lie
algebras to Γ, through their first Chevalley-Eilenberg cohomology spaces,
namely, the Lie algebra of vector fields AΓ on TM, whose Lie derivative
applied to Γ is zero, and the horizontal nullity space 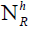 of the curvature
R of Γ
of the curvature
R of Γ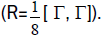 The Lie algebra AΓ is formed by projectable vector
fields, and contains two ideals
The Lie algebra AΓ is formed by projectable vector
fields, and contains two ideals 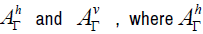 consists of
projectable vector fields of the horizontal nullity space of the curvature R
and
consists of
projectable vector fields of the horizontal nullity space of the curvature R
and 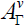 an ideal of the vertical space.
an ideal of the vertical space.
In [6], Loos O. considered a spray S as a system of second order
differential equations on M. If we denote by AS the Lie algebra of vector
fields on TM which commute with S, the projectable vector fields of AS correspond to 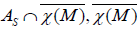 being the complete lift on the tangent bundle TM of the set of all vector fields χ(M) on M. We will denote the set
being the complete lift on the tangent bundle TM of the set of all vector fields χ(M) on M. We will denote the set  such that
such that 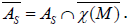 The Lie algebra
The Lie algebra  corresponds to a Lie
group GS of transformations on M of which the tangent linear mappings
preserve the spray S. The group GS acts freely on the linear frame bundle
of M. The dimension of
corresponds to a Lie
group GS of transformations on M of which the tangent linear mappings
preserve the spray S. The group GS acts freely on the linear frame bundle
of M. The dimension of  is at most equals to n2+n.
is at most equals to n2+n.
In the following, a connection Γ is linear without torsion, in this case
[3], Γ is written: Γ=[J, S] and [C, S]=S, where C being the Liouville field
on TM. We prove that 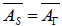 by considering
by considering 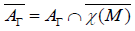 . For a linear connection without torsion such that the rank of the horizontal nullity
space of the projectable vector fields of curvature R is nonzero constant,
the Lie algebra
. For a linear connection without torsion such that the rank of the horizontal nullity
space of the projectable vector fields of curvature R is nonzero constant,
the Lie algebra 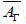 . All the commutative ideals of
. All the commutative ideals of 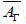 do not
always come from the horizontal nullity space of the curvature for any spray
S. Let E be an energy function [3], that is to say, a mapping
do not
always come from the horizontal nullity space of the curvature for any spray
S. Let E be an energy function [3], that is to say, a mapping 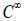 on TM to
on TM to 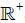 , null on the null section, homogeneous of degree two (LCE=2E), LC being the Lie derivative with respect to C, such that the 2-form Ω=ddJE is of
maximum rank. The canonical spray S is defined [5] by
, null on the null section, homogeneous of degree two (LCE=2E), LC being the Lie derivative with respect to C, such that the 2-form Ω=ddJE is of
maximum rank. The canonical spray S is defined [5] by
isddjE=-dE, iS being the inner product with respect to S. The 2-form Ω defines a
Riemannian metric on the vertical bundle. In local coordinate system on an
open set U of M, 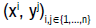 , the coordinate system on TU , the function
E is written
, the coordinate system on TU , the function
E is written
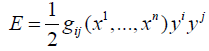
where 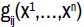 are positive functions such that the symmetric matrix
are positive functions such that the symmetric matrix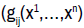 is invertible . We denote by g
is invertible . We denote by g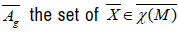 such that
such that 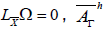 is a commutative ideal of
is a commutative ideal of 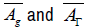 . We then have the
following algebra inclusions:
. We then have the
following algebra inclusions: 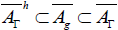 . The dimension of
. The dimension of 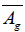 is at
most equal to
is at
most equal to 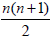 . The
. The 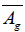 is also the Lie algebra of the Killing fields of
projectable vectors which commute with the spray S. If the dimension of
is also the Lie algebra of the Killing fields of
projectable vectors which commute with the spray S. If the dimension of 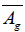 is greater than or equal to three, the Lie algebra
is greater than or equal to three, the Lie algebra 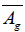 is semi-simple if and
only if the horizontal nullity space of the Nijenhuis tensor of Γ is reduced
to zero. In this context, the algebra
is semi-simple if and
only if the horizontal nullity space of the Nijenhuis tensor of Γ is reduced
to zero. In this context, the algebra 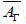 coincides with
coincides with 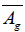 . It follows that
for the flat Riemannian manifolds (R=0), the Lie algebra
. It follows that
for the flat Riemannian manifolds (R=0), the Lie algebra 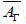 , the Killing algebra
, the Killing algebra 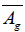 also, contain commutative ideals. For Riemannian manifolds
with nonzero constant sectional curvature,
also, contain commutative ideals. For Riemannian manifolds
with nonzero constant sectional curvature, 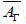 is the isometry algebra
is the isometry algebra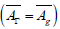 , and it is semi-simple.
, and it is semi-simple.
This study also makes it possible to construct numerous examples of Lie algebra containing a commutative ideal. In particular, for a semi-simple Lie algebra, the derivative ideal coincides with algebra. This examples show that this property is not sufficient to be a semi-simple Lie algebra.
This paper is part of the continuation of the studies made in [5,7-9].
We will recall the bracket of two vector 1-form K and L on a manifold M [1]. If we denote χ(M) the set of vector fields on M,
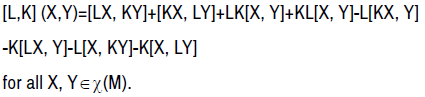 (2.1)
(2.1)
The bracket NL=1/2 [L, L] is called the Nijenhuis tensor of L. The Lie derivative with respect to X applied to L is written:
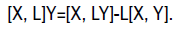
The exterior differentiation dL is defined by 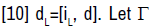 be a
connection. By
be a
connection. By
h=1/2(I+ Γ) and v=1/2(I-Γ),
h is the horizontal projector, projector of the subspace corresponding to the eigenvalue +1, v the vertical projector corresponding to the eigenvalue -1. The curvature of Γ is defined by
R=1/2 [h,h];
which is equal to
R=1/8 [Γ, Γ].
The Lie algebra AΓ is written
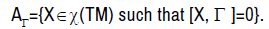
The nullity space of the curvature R is written:
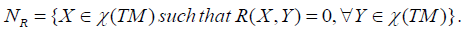
According to the results of [5], the elements of AΓ are projectable
vectors fields. The horizontal and vertical parts of AΓ respectively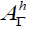 and
and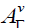 are ideals of AΓ . If we denote by H° the set of horizontal and
projectable vector fields, then we have
are ideals of AΓ . If we denote by H° the set of horizontal and
projectable vector fields, then we have
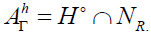 (2.2)
(2.2)
Definition 1 [3]
We call strong torsion T of Γ the vector 1-form
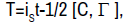
where S indicates a spray, t=1/2 [J, Γ ] called weak torsion of Γ, iS the inner product with respect to a spray S.
We recall a result of [3] on the decomposition of a connection
Γ=[J, S]+T.
The elements of 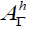 are well known [5]. In the following section, we
will be interested in the ideal
are well known [5]. In the following section, we
will be interested in the ideal 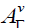 .
.
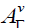
A vertical vector field can be written in the form JX, J being the tangent structure on TM, and X a horizontal vector field.
Proposition 1 [5]
A vertical vector field JX is an element of 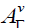 if and only if JX commutes
with all horizontal and projectable vector fields.
if and only if JX commutes
with all horizontal and projectable vector fields.
Proposition 2
Let Γ be a zero weak torsion connection, X and Y two horizontal vector
fields such that JX and JY are elements of 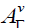 . So we have
. So we have
J [X, Y]=0.
In particular,
[X, Y]=R(X, Y).
Proof: The nullity of the weak torsion of Γ allows to write
v [JX, Y]+v [X, JY]=J [X, Y], (3.1)
for all X, Y horizontal vector fields. If JX and JY are two elements of 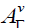 , we get v [JX, Y]=0 and v [X, JY]=0, that is to say
, we get v [JX, Y]=0 and v [X, JY]=0, that is to say
J [X, Y]=0.
This means that the horizontal part of [X, Y] is zero, we find
[X, Y]=v [X, Y]=R (X, Y).
Proposition 3
Let Γ be a zero weak torsion connection, X a horizontal vector field. The two following conditions are equivalent:
a) X is a projectable vector field and [JX, h]=0;
b) [X, J]=0.
Proof: The nullity of the weak torsion of Γ is written:
[JX, h]Y+[X, J]Y=h[X, JY], (3.2)
for all horizontal vector fields X, Y. If X is projectable, the term
h [X, JY] is zero; and if [JX, h]=0, we get [X, J]Y=0, for all horizontal
vector fields Y. If Y is a vertical vector field, we have [X, J] Y=0,
since X is projectable. This proves that the relation a) implies b).
If [X, J]=0, the horizontal vector field X is projectable [11], so we have h
[X, JY]=0; and the nullity of the weak torsion of Γ (3.2) results in [JX, h]=0.
In the following section, we assume that the connection
Γ has a null strong torsion, that is, Γ=[J, S] and [C, S]=S.
Einstein’s convention on the summation of indices will be adopted. In natural
local coordinates on an open set U of M, 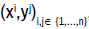 , the coordinates on
TU, a spray S is written:
, the coordinates on
TU, a spray S is written:
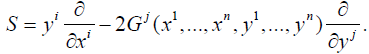
For a connection ΓΓ =[J, S], the coefficients of Γ become 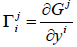 and the horizontal projector is
and the horizontal projector is
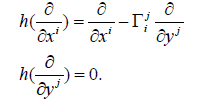
The vertical projector is written:
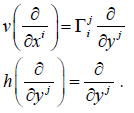
The curvature R=1/2 [h, h] become
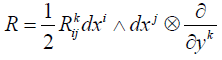
With 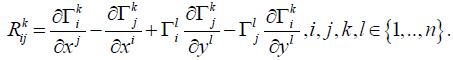
We can associate with Γ a linear connection 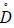 on TM, called Berwald
connection [4] with curvature
on TM, called Berwald
connection [4] with curvature
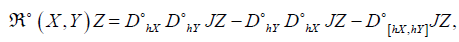
for all X, Y and Z ∈χ(TM). The curvature R of Γ is linked to  by the
relation:
by the
relation:

[JZ, R(X ,Y)]+ R([JZ, X ],Y) + R(X ,[JZ,Y])
In particular,
 (X ,Y)S = −R(X ,Y).
(X ,Y)S = −R(X ,Y).
Proposition 4
Let JX 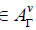 such that X be a projectable vector field, then we have
such that X be a projectable vector field, then we have
 (Y, Z)X = 0,
(Y, Z)X = 0,
for all Y, Z ∈χ(TM).
Proof: Let JX 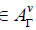 . This means [JX,h]=0. According the expression
of R=1/2 [h, h] and the identity of Jacobi, we get [JX,R]=0. In other words,
for all Y, Z ∈χ(TM), we have
. This means [JX,h]=0. According the expression
of R=1/2 [h, h] and the identity of Jacobi, we get [JX,R]=0. In other words,
for all Y, Z ∈χ(TM), we have
[JX, R(Y, Z)]-R([JX, Y], Z)-R(Y,[JX, Z])=0.
So the expression of  becomes
becomes
 (Y, Z)X = J[X , R(Y, Z)].
(Y, Z)X = J[X , R(Y, Z)].
The vector field X being projectable and R(Y, Z) vertical, the second
member of the equality is null. So we find  (Y, Z)X = 0.
(Y, Z)X = 0.
Let 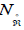 be the nullity space of
be the nullity space of 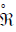 , Ker
, Ker 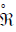 the kernel of
the kernel of 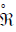 :
:
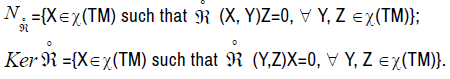
Proposition 5
The horizontal ideal 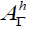 of AΓ becomes
of AΓ becomes
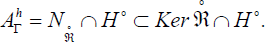
Proof: According to the relation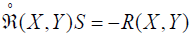 for all X, Y
∈χ(TM), we have
for all X, Y
∈χ(TM), we have
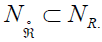
If X 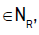 according to the previous relationship between
according to the previous relationship between  and R, we get
and R, we get
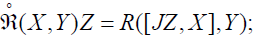
if X is projectable, [JZ, X] is vertical and R ([JZ, X], Y) is therefore zero. This results in
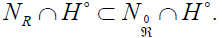
In conformity with a result of [5], we have
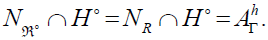
Bianchi identity on  is written [4]:
is written [4]:

Proposition 6
If the module NR ∩ H° on the ring of constant functions to the fibers is
of nonzero and constant rank, there is locally a non-trivial vector field such
that 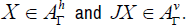
Proof: We will solve the equation
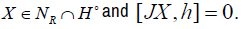 (3.4)
(3.4)
This leads to solving, according to the proposition 3, the equations
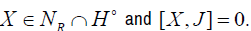
In other words, X is a horizontal and projectable vector field of the nullity space belonging to the Lie algebra AJ. The elements of AJ are well known [11]. We can write in local coordinates:
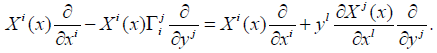
For a linear connection, we have 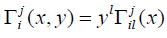 , the system of
equations to be solved becomes
, the system of
equations to be solved becomes
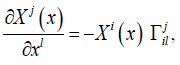 (3.5)
(3.5)
with i, j, l ∈{1,…,n} . The compatibility condition of the equation (3.5), according to the Frobenius theorem, is
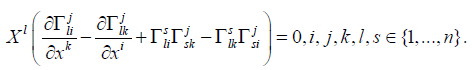
This condition is nothing but 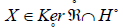 and according to the
proposition 5, we have
and according to the
proposition 5, we have 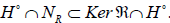 If the rank
If the rank 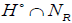 is
nonzero constant,
is
nonzero constant, 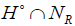 defines a foliation. On a submanifold defined
by the distribution
defines a foliation. On a submanifold defined
by the distribution 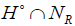 the equation (3.5) admits a non-trivial
solution.
the equation (3.5) admits a non-trivial
solution.
Proposition 7
Let B be the set defined by
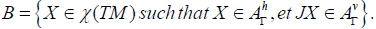
Then B+JB is a commutative subalgebra of 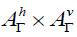 and a
commutative ideal of
and a
commutative ideal of 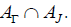
Proof: On the one hand, let X and Y be two elements of B, according to the proposition 2, we have
[X, Y]=0
On the other hand, X and Y being projectable, we find
[JX, JY]=0.
It is obvious that B is a subalgebra of 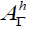 , and JB a subalgebra of
, and JB a subalgebra of 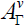 . Consequently, B+JB is a commutative subalgebra of
. Consequently, B+JB is a commutative subalgebra of 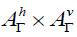 and of AΓ .
and of AΓ .
If Y ∈ AΓ ∩ AJ, for X ∈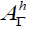 , we have
, we have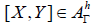 since
since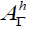 is an ideal of AΓ. Now let us prove
is an ideal of AΓ. Now let us prove 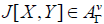 , that is,
[J[X, Y], h]=0. According to the proposition 3, this leads to prove that [[X, Y],
J]=0 and [X, Y] is a horizontal vector field, which is immediate by the identity
of Jacobi and X ∈
, that is,
[J[X, Y], h]=0. According to the proposition 3, this leads to prove that [[X, Y],
J]=0 and [X, Y] is a horizontal vector field, which is immediate by the identity
of Jacobi and X ∈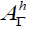 , horizontal ideal of AΓ .
, horizontal ideal of AΓ .
The Lie algebra AJ is well known [11], and it is written
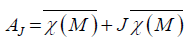
in which 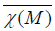 denotes the complete lift on the tangent bundle TM of
χ(M). We denote AS ={X ∈χ(TM) such that [X, S]=0}.
denotes the complete lift on the tangent bundle TM of
χ(M). We denote AS ={X ∈χ(TM) such that [X, S]=0}.
Proposition 8
The vertical vectors fields of AS are trivial.
Proof: A vertical vector field is of the form JX, where X ∈ χ(TM). JX is an element of AS if [JX, S]=0. In conformity with the formula J [JX, S]=JX for all X ∈ χ(TM), the previous relation implies JX=0 for all JX ∈ AS.
Proposition 9
The set of projectable vector fields of AS coincides with 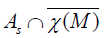 and that
and that 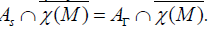
Proof: Let X be a projectable vectors field, the identity of Jacobi makes it possible to write
[J, [X, S]]+[X, [S, J]]+[S, [J, X]]=0.
If [X, S]=0, the above relation becomes
[[J, S], X]=[[J, X], S]. (4.1)
But we have Γ=[J, S], Γh=h, Γv=-v and h+v=I, we find
[Γ, X]Y=[ΓY, X] -Γ [Y, X]=2v[Y, X],
for all Y horizontal vector field of Γ . On the other hand, we have
[S, [J, X]] Y=[S, [J, X]Y]-[J, X] [S, Y].
As [J, X] [S, Y] and [J, X] Y are vertical since X is projectable, by applying J to the relation (4.1) we find
[J, X] Y=0, (4.2)
for all Y horizontal vectors field. If Y is vertical, it is immediate to note that
[J, X] Y=0. (4.3)
The relations (4.2) and (4.3) prove that [J, X]=0. In other words, X ∈ AJ. But 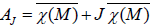 , M , and taking into account the proposition
8, therefore, the set of projectable vector fields of AS coincides with
, M , and taking into account the proposition
8, therefore, the set of projectable vector fields of AS coincides with 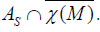
With [J, X]=0, the relation (4.1) proves that X ∈ AΓ . That is to say
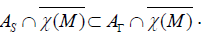
Let us now prove that 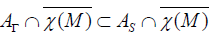 .
.
Let be 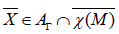 This results in
This results in 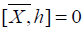 with S=hS. If we
apply to S the above relation, we get
with S=hS. If we
apply to S the above relation, we get
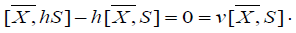 (4.4)
(4.4)
From the relation 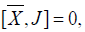 we find
we find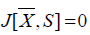 . In other words,
taking into account that h is semi-basic
. In other words,
taking into account that h is semi-basic
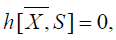 (4.5)
(4.5)
as v+h=I, the two relations (4.4) and (4.5) result in
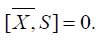
Which proves that
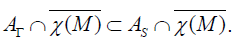
Remark 1: The proposition 9 is contained in [12] in another way.
In the following, we assume 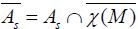 and
and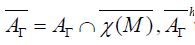 the horizontal part of
the horizontal part of 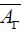 .
.
Proposition 10
The horizontal part of 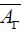 is such that
is such that
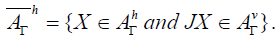
and 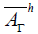 is a commutative ideal of the Lie algebra
is a commutative ideal of the Lie algebra 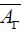 .
.
Proof: This is to prove that the horizontal part of 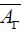 is only the B of the
proposition 7, which is immediate according to the proposition 3.
is only the B of the
proposition 7, which is immediate according to the proposition 3.
Theorem 1
For all differentiable manifold of n dimension with a linear connection
without torsion such that the rank of the nullity space of the projectable vector fields of the curvature is nonzero constant, the Lie algebra 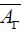 contains a nonzero commutative ideal formed by the horizontal part of
contains a nonzero commutative ideal formed by the horizontal part of 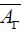 .
.
Proof: This is the consequence of previous studies. The existence of
the nonzero horizontal part of 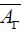 is given by the proposition 6.
is given by the proposition 6.
We denote by GS the set of diffeomorphisms φ of M such that the
induced diffeomorphisms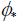 on TM preserve a spray S, GS forms a group.
From the study of the equations of AS and GS on a local coordinate
system of M, using the classical theorem of Palais, Loos O. [6] deduces
the following result:
on TM preserve a spray S, GS forms a group.
From the study of the equations of AS and GS on a local coordinate
system of M, using the classical theorem of Palais, Loos O. [6] deduces
the following result:
Theorem 2 [6]
a) GS acts freely on the linear frame bundle of M. In particular, the
dimension of  is less than or equals to n2+n.
is less than or equals to n2+n.
b) There exists a unique Lie group structure on GS such that GS is a
Lie transformation group of M with Lie algebra the set of complete vector
fields in 
c) If the dimension of  =n2+n and M a manifold simply connected,
then (M, S) is isomorphic to
=n2+n and M a manifold simply connected,
then (M, S) is isomorphic to 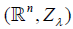 for an unique
for an unique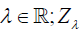 is given by
the equations
is given by
the equations 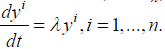
Example 1
Let be 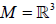 and the connection Γ=[J, S] with
and the connection Γ=[J, S] with
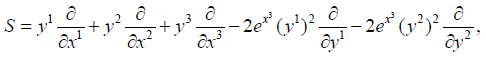
then the coefficients of Γ being  the nonzero
coefficients of the connection are
the nonzero
coefficients of the connection are 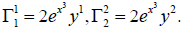
The horizontal space is generated by
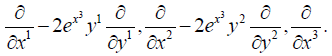
We notice that 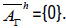 The Lie algebra
The Lie algebra 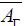 is generated by
is generated by
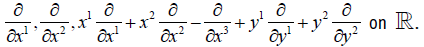
We note that all the subalgebras of 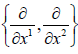 are commutative ideals
of
are commutative ideals
of 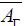 .
.
None of these nonzero ideals are horizontal.
Example 2
Let E be the energy function such that
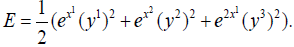 The canonical spray is written:
The canonical spray is written:
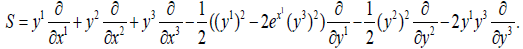
The nonzero coefficients of the connection are
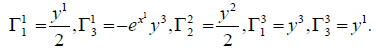
The horizontal vector fields are generated by
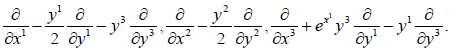
The horizontal nullity space of the curvature is generated by 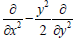 .
.
The elements of 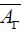 are generated by
are generated by
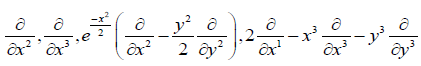
The commutative ideal is generated by 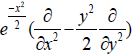 .
.
We note that for any linear connection (see the example 1), the commutative ideals do not always come from the horizontal nullity space of the curvature.
The example 2 shows that the commutative ideal is of the horizontal nullity space of the curvature. The question is to know if it is true for all canonical connection coming from an energy function in the language of [3]. This is the object of our study.
In this paragraph, we are content to state the well-known results on the Riemannian manifolds which will be used.
Definition 2
We call the Riemannian manifold, the couple (M, E):
• M is a differentiable manifold;
• E a function of  on
TM,
on
TM,  on the null section, and homogeneous of degree two, such that
ddJE has a maximum rank.
on the null section, and homogeneous of degree two, such that
ddJE has a maximum rank.
We notice that if E is of class 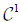 on the null section, we will have a
Finsler manifold. Imposing E of class
on the null section, we will have a
Finsler manifold. Imposing E of class 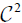 on the null section implies that the
function E is of class
on the null section implies that the
function E is of class 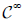 on TM.
on TM.
The application E is called energy function, Ω=ddJE its fundamental form defines a spray S [13]:
iSddJE=-dE and Γ=[J, S] is called canonical connection. (7.1)
The fundamental form Ω allows to define a metric g on the tangent bundle by
g (X, Y)=Ω (X, FY), (7.2)
X and Y being two vector fields on TM, F the almost complex structure
associated with Γ, (FJ=h and Fh=-J where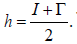 There is, [4], one and
only one metric lift D of the canonical connection such that:
There is, [4], one and
only one metric lift D of the canonical connection such that:
1. 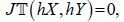
2. 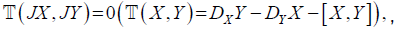
3. DJ=0,
4. DC=v,
5. DΓ=0,
6. Dg=0,
7. DF=0.
The linear connection D is called Cartan connection. For a Riemannian
manifold, the Cartan connection D and the Berwald connection 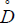 are
identical. We have
are
identical. We have
DJXJY=[J, JY] X, DhXJY=[h, JY] X.
To the linear connection D, we associate a curvature
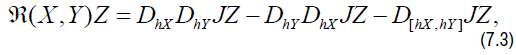
for all X, Y, Z ∈ χ(TM). In particular,
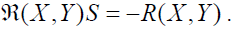 (7.4)
(7.4)
In natural local coordinates on an open set U of M, (xi, yj) ∈TU ∈ i, j ∈ {1,..., n} , the energy function is written [3] p.330
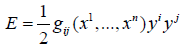
where 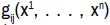 are symmetric positive functions such that the
matrix
are symmetric positive functions such that the
matrix 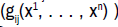 is invertible . the relation iSddJE=-dE gives the
spray S,
is invertible . the relation iSddJE=-dE gives the
spray S,
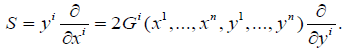
with 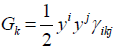
where 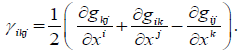
By 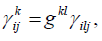
we have 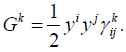
The relation (7.1) is equivalent to the following relation
dhE=0. (7.5)
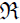 of a Riemannian Man
of a Riemannian ManFrom the properties stated above, we obtain the following classic results: for all X, Y, Z, T ∈ χ(TM)
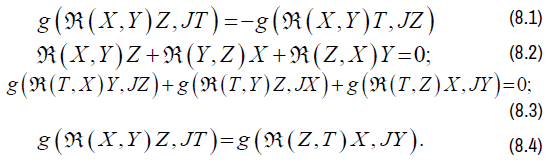
From the properties of the curvatures given above, we have:
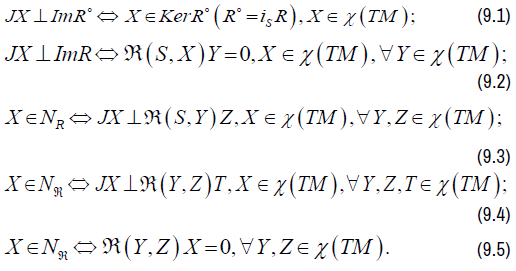
Proposition 11
On a Riemannian manifold, the horizontal ideal 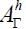 of the Lie algebra AΓ satisfies
of the Lie algebra AΓ satisfies
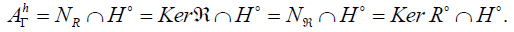
Proof: According to the proposition 5, the horizontal ideal AΓ of AΓ is written
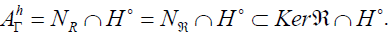
From the relation (8.4), we get 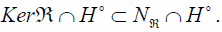 It
remains to prove that
It
remains to prove that
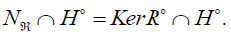
It is immediate to notice that
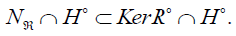
Let be  According to the relation (9.1), we have for all
According to the relation (9.1), we have for all
Y ∈χ(TM),
g (Rο (Y), JX)=0.
As Dg=0, we get
g ([J, Rο (Y)]Z, JX)=-g(Rο (Y), [J, JX]Z).
The vector field X being projectable, [J, JX]=0, we have
g ([J, Rο (Y)]Z, JX)=0.
From the relation (8.2), namely: namely:
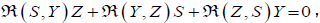 we conclude
we conclude
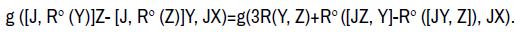
According to the relation (9.6) and that JX is orthogonal to Im Rο, we find
g (R(Y, Z ), JX ) = 0,
that is, JX⊥ ImR. Taking into account DJT g=0, and X a projectable vectors field, we have
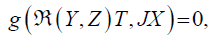
that is, 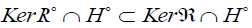
Proposition 12
On a Riemannian manifold, the three following relations are equivalent:
i. the horizontal nullity of the curvature R is reduced to zero
ii. the horizontal nullity space of the projectable vector fields of R is reduced to zero
iii. the dimension of the image space of the curvature R is equal to n-1
Proof: If the horizontal nullity space of the projectable vector fields
is not reduced to zero, there will be a nonzero horizontal and projectable
vector field X, according to the proposition 11, such that 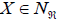 , and according to the relation (9.4), JX is orthogonal to
, and according to the relation (9.4), JX is orthogonal to 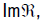 therefore
orthogonal to ImR according to the relation (7.4). The image space of
the curvature R is both orthogonal to JX and to the Liouville field C=JS
with JX ∧ C ≠ 0. This is only possible if the dimension of the image
space of R is strictly less than n-1.. So the relation (iii) implies (ii).
We notice by (7.5) that dRE=0. That is, the image space of R is in the
kernel of dE. If the dimension of the image space of the curvature R is
strictly less than n-1, there will be a horizontal vector field X such that
JX ∈ KerdE and JX ⊥ ImR. According to the relation (9.2), we have
therefore
orthogonal to ImR according to the relation (7.4). The image space of
the curvature R is both orthogonal to JX and to the Liouville field C=JS
with JX ∧ C ≠ 0. This is only possible if the dimension of the image
space of R is strictly less than n-1.. So the relation (iii) implies (ii).
We notice by (7.5) that dRE=0. That is, the image space of R is in the
kernel of dE. If the dimension of the image space of the curvature R is
strictly less than n-1, there will be a horizontal vector field X such that
JX ∈ KerdE and JX ⊥ ImR. According to the relation (9.2), we have 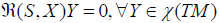 . By developing this equality and taking into
account the relation (9.1), we have R(X, Y)=Rο[JY, X] ∀Y ∈χ(TM).. This is
only possible if X=S or X∈ NR. Since, JX ⊥C, therefore, we have X∈ NR.
. By developing this equality and taking into
account the relation (9.1), we have R(X, Y)=Rο[JY, X] ∀Y ∈χ(TM).. This is
only possible if X=S or X∈ NR. Since, JX ⊥C, therefore, we have X∈ NR.
This last calculation proves at the same time that the horizontal nullity space of R is generated by projectable vectors field belonging to NR. Consequently, we have (i)=⇒ (iii) and (ii)=⇒ (i).
Definition 3
Let ω be a p-differential form defined on a manifold M. A conformal infinitesimal transformation of ω is a vector field X defined on M, such that for all elements (t, x) of the domain D(X) of the flow Φ of X, we have
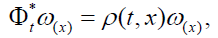
where ρ is a differentiable numeric function, with positive values, defined on D(X).
We have the following result:
Proposition 13
For a vector field X to be a conformal infinitesimal transformation of p-differential form ω, it is necessary and sufficient that we have,
LXω=λω,
where LX is the Lie derivative with respect to X and λ a differentiable numerical function defined on M. When this is the case, the function λ is linked to the function ρ which appears in the definition 3, by the relation
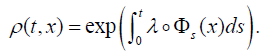
In the following, we are interested in conformal transformations of the fundamental form Ω of a Riemannian manifold.
Proposition 14
If X is a conformal infinitesimal transformation of Ω, i.e.
LXΩ=λΩ,then λ is a constant function.
Proof: Let be X a vector field belonging to χ(TM) such that
LXΩ=λΩ,
with 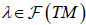 the set of differentiable functions on TM. Since
Ω=ddJE, we have
the set of differentiable functions on TM. Since
Ω=ddJE, we have
λddJE=dLXdJE.
The expression λddJE is an exact 2-form, this implies
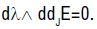 (10.1)
(10.1)
as ddJE is of maximum rank and the dimension of the manifold M is assumed to be greater than or equal to two, the relation (10.1) results in
dλ=0.
In other words, the function λ is a constant.
In the following, we will denote Agc the set of conformal infinitesimal
transformations of Ω and 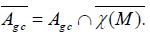
Proposition 15
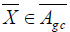 if and only if
if and only if
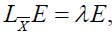
where λ is a constant given by the relation . 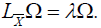
Proof: Let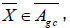 we have
we have
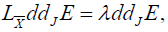
where λ is a constant according to the proposition 14. As the two
derivations 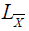 and dJ commute, we obtain
and dJ commute, we obtain
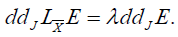
By derivating by iC, the two 2-forms above, C being Liouville field, we find
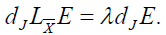
The application of iS to the above equality gives
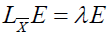
Conversely, if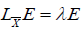 with
with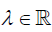 , it is immediate to
note that by continuing the previous calculation, we have
, it is immediate to
note that by continuing the previous calculation, we have
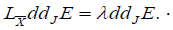
Proposition 16
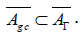
Proof: Let 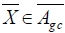 . Since iSddJE=-dE, we can write successively
. Since iSddJE=-dE, we can write successively
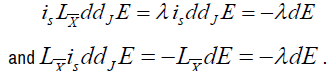
From the formula  we get
we get
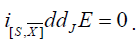
As ddJE is a symplectic form, we find
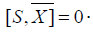
This means that 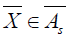 . For a Riemannian manifold,
. For a Riemannian manifold,
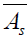 coincides with
coincides with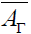 . Thus,
. Thus,
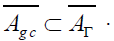
Proposition 17
Let F be the almost complex structure associated to Γ . So by noting
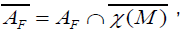
we have
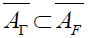 .
.
Proof: Let 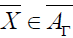 . According to the definition of F, namely,
. According to the definition of F, namely,
FJ=h and Fh=-J,
we can write successively for all Y ∈χ(TM)
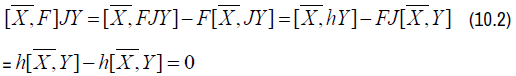
Similarly, we have
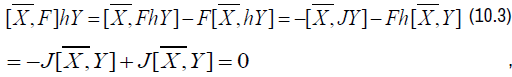
for all Y ∈χ(TM), the two relations (10.2) and (10.3) lead to
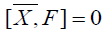 .
.
In other words,
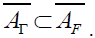
Proposition 18
Let 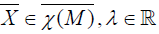 .So
.So
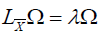 is equivalent to
is equivalent to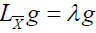 .
.
Proof: a) Suppose 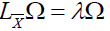 , we have
, we have

for all Y, Z∈χ(TM). Given the relation g(Y, Z)=Ω(Y, FZ), the second member of the above equality becomes
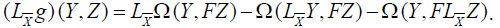
By taking into account the propositions 16 and 17, we obtain
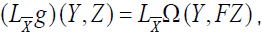
for all Y, Z ∈χ(TM). If 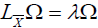 , we find
, we find
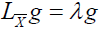 .
.
b) Suppose 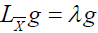 . We have
. We have
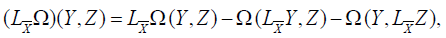 (10.4)
(10.4)
for all Y, Z ∈χ(TM). The expression of Ω in function of g is [3]
Ω (Y, Z)=g (Y, JZ)+g (JY, Z), (10.5)
for all Y, Z ∈χ(TM).. The expression (10.4) becomes
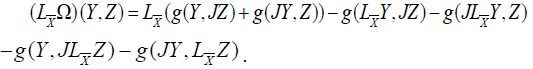
As 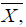 belongs to AJ, we get
belongs to AJ, we get
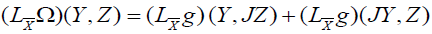 .
.
If 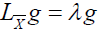 , taking into account the relation (10.5) we find
, taking into account the relation (10.5) we find
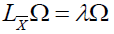 .
.
Definition 4
A vector field X on a Riemannian manifold (M, E) is said to be infinitesimal automorphism of the symplectic form Ω if
LXΩ=0.
We notice the canonical spray S of (M, E) is an infinitesimal automorphism of the symplectic form Ω.
The set of infinitesimal automorphisms of Ω forms a Lie algebra. We will denote this Lie algebra by Ag.
Proposition 19
By supposing 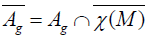 , we have
, we have
a) 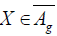 if and only if X is a projectable vector field such that X ∈Ag and LXE=0;
if and only if X is a projectable vector field such that X ∈Ag and LXE=0;
b) 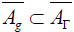 ; the horizontal elements of
; the horizontal elements of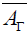 form a commutative ideal
of
form a commutative ideal
of  .
.
c) The elements of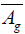 are Killing fields of projectable vectors of
the metric g belonging to
are Killing fields of projectable vectors of
the metric g belonging to 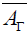 . The dimension of
. The dimension of 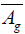 is at most equal to
is at most equal to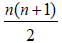 .
.
Proof: It is clear that if 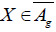 then LXE=0. This is a particular case of
the proposition 15 for λ=0.
then LXE=0. This is a particular case of
the proposition 15 for λ=0.
Let X be a projectable vector field such that LXΩ=0 and LXE=0, we
will prove that 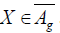 . The fundamental form Ω is written Ω=ddJE,
as LXΩ=0, we have
. The fundamental form Ω is written Ω=ddJE,
as LXΩ=0, we have
iSLXΩ=0.
Besides, according to the relation (7.1) and the hypothesis LXE=0 LXiSΩ=-dLXE=0. According to the formula i[S,X]=iSLX-LXiS, we find i[S,X]Ω=0.
Since the fundamental form Ω is symplectic, we get [S, X]=0. The vector field X being projectable by hypothesis, according to the proposition
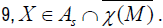
-The result of b) is a consequence of the proposition 16 because 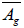 is a particular case of
is a particular case of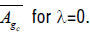 Since, we have by (7.5), the horizontal
elements of
Since, we have by (7.5), the horizontal
elements of 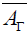 belong to
belong to  and form a commutative ideal of
and form a commutative ideal of  , according to the theorem 1.
, according to the theorem 1.
- Finally, the property c) is given by the proposition 18 by taking λ=0.
In addition, g defines a metric on the vertical bundle which is of n
dimension. The flow Φ of a vector field 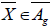 is a local isometry for g.
Consequently, Φ preserves the orthogonal bases of g on the vertical
bundle. With the method used in theorem 3.3 of [14] vol.1 p.238, the
dimension of
is a local isometry for g.
Consequently, Φ preserves the orthogonal bases of g on the vertical
bundle. With the method used in theorem 3.3 of [14] vol.1 p.238, the
dimension of  is at most equal to
is at most equal to 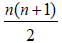 .
.
Theorem 3
Let (M, E) be a Riemannian manifold with a nonzero constant sectional
curvature. Then  coincides with
coincides with 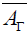 .
.
Proof: If the sectional curvature K is constant, we have [2]
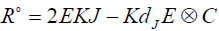
where 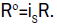 For all
For all 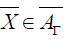 , we have
, we have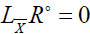 . If K is not zero,
we get
. If K is not zero,
we get 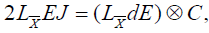
this is only possible if 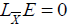 , that is, according to the proposition 19
, that is, according to the proposition 19
a), 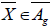 . In other words,
. In other words,
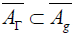 .
.
The proposition 19 b) gives
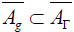 .
.
Definition 5
We will say that a connection Γ has a regular curvature at a point z of TM if the vector space generated by the image of the curvature Rz is of n-1 dimension.
Proposition 20
Let (M, E) be a Riemannian manifold such that
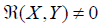 for all horizontal vector fields X, Y linearly independent,
then (M, E) has a regular curvature.
for all horizontal vector fields X, Y linearly independent,
then (M, E) has a regular curvature.
Proof: The dimension of ImR is less than or equal to n-1, since the canonical field C=JS is orthogonal to ImR.
If the dimension of ImR is less than or equal to n-2, there will be a horizontal vector field Z such that JZ ⊥ ImR and S ∧ Z ≠ 0, and according to the relation (9.2), we would have
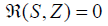
this contradicts the hypothesis.
Remark 2: The converse of the proposition 20 is not true in general.
Theorem 4
Let (M, E) be a Riemannian manifold, Γ a canonical connection of (M, E) with regular curvature. So
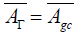 .
.
Proof: The proposition 16 gives
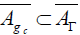 .
.
It remains to prove that 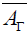 is contained in
is contained in 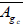 ; and for that, it is
simply sufficient to prove
; and for that, it is
simply sufficient to prove 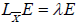 for all
for all 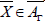 ,
,  according
to the proposition 15.
according
to the proposition 15.
Let 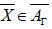 as AΓ is identical to Ah, we have
as AΓ is identical to Ah, we have
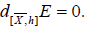
According to the formula 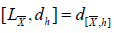 and by (7.5), we obtain
and by (7.5), we obtain
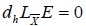 . (12.1)
. (12.1)
That implies
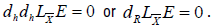
Let H be the horizontal space of Γ, H ⊕ImR is contained in the
kernel of dE. By hypothesis, the curvature R is regular, so H ⊕ ImR is of
2n-1 dimension, and the kernel of dE. Therefore, H ⊕ ImR is a completely
integrable distribution. According to Frobenius theorem, at each point z of
TM, it passes a maximum integral manifold which is the solution of the
equation (12.1). We notice that 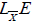 is homogeneous of degree two and
that the function
is homogeneous of degree two and
that the function 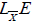 is continuous and null on the null section.
is continuous and null on the null section.
This imposes the initial conditions for the solutions of the equation (12.1). Hence the result
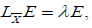
With λ is a constant.
Remark 3: A Riemannian manifold with a constant and nonzero sectional curvature has a regular curvature, but the value of λ is zero. The theorem 3 excludes the case of λ ≠ 0.
Proposition 21
Let (M, E) be a Riemannian manifold with regular curvature, Rο=iSR, we have the following relation:
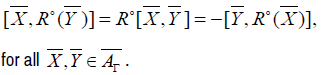
Proof: For all 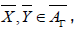 we have
we have
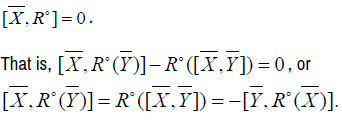
Theorem 5
The Lie algebra  of the Killing fields contained in
of the Killing fields contained in 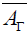 of dimension
greater than or equal to three is semi-simple if and only if the Riemannian
manifold is with regular curvature.
of dimension
greater than or equal to three is semi-simple if and only if the Riemannian
manifold is with regular curvature.
Proof: If the Riemannian manifold is not with regular curvature, there is
the horizontal nullity space of the projectable vector fields of the curvature R
which provides the commutative ideal of 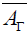 , according to the propositions
19 b) and 12, which is also that of
, according to the propositions
19 b) and 12, which is also that of  . Then
. Then  is not semi- simple.
is not semi- simple.
It is assumed that the Riemannian manifold has a regular curvature. Let 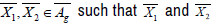 are linearly independent. As the mapping
are linearly independent. As the mapping 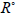 is injective on the projectable vector fields according to the proposition
11 and the definition 5.
is injective on the projectable vector fields according to the proposition
11 and the definition 5. 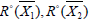 are also linearly independent.
are also linearly independent.
According to the proposition 21,
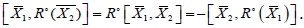
As 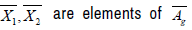 we have the following system of
equations
we have the following system of
equations
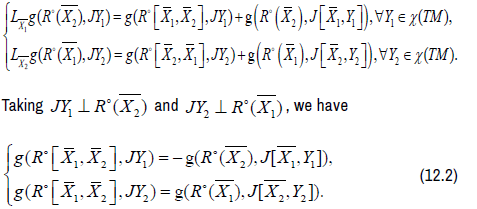
If we have  linearly independent, we have
linearly independent, we have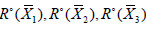 linearly independent, and we have a system of six
equations as (12.2). For
linearly independent, and we have a system of six
equations as (12.2). For 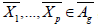 , we have a system of 2p equations
as (12.2). Such a system of equations do not allow us to have a commutative
ideal of
, we have a system of 2p equations
as (12.2). Such a system of equations do not allow us to have a commutative
ideal of  other than zero.
other than zero.
We conclude that if  is of dimension superior or equals to three for a
Riemannian manifold with regular curvature,
is of dimension superior or equals to three for a
Riemannian manifold with regular curvature, is semi-simple.
is semi-simple.
Corollary 1
On a Riemannian manifold (M, E) of n ≥ 2 dimension, the Lie algebra  of infinitesimal isometries contained in
of infinitesimal isometries contained in 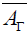 of dimension superior or
equals to three is semi-simple if and only if the horizontal nullity space of
the Nijenhuis tensor of Γ is reduced to zero. In this case, the Lie algebra
of dimension superior or
equals to three is semi-simple if and only if the horizontal nullity space of
the Nijenhuis tensor of Γ is reduced to zero. In this case, the Lie algebra 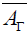 coincides with
coincides with  .
.
Proof: The reasoning used in the theorem 5 is based on the existence
of two linearly independent elements of .  So the dimension of
So the dimension of  is
assumed to be superior or equals to two. We know that there is no semisimple
Lie algebra of one or two dimension. Hence, the condition of the
dimension of
is
assumed to be superior or equals to two. We know that there is no semisimple
Lie algebra of one or two dimension. Hence, the condition of the
dimension of  superior or equals to three.
superior or equals to three.
We notice the interlocking of the algebras 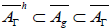 . So if the
dimension of
. So if the
dimension of  is superior or equals to three, for a Riemannian manifold
with regular curvature, according to the theorem 5,
is superior or equals to three, for a Riemannian manifold
with regular curvature, according to the theorem 5,  is semi-simple. In
this case, according to the theorem
is semi-simple. In
this case, according to the theorem 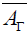 =
=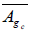 and
and  is an ideal of
is an ideal of 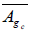 . Consequently
. Consequently  =
= 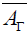 , otherwise we have a contradiction.
, otherwise we have a contradiction.
Remark 4: If the Riemannian manifold is flat (R=0), the horizontal
elements of 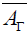 constitute a nonzero commutative ideal of
constitute a nonzero commutative ideal of  . If the
Riemannian manifold has a nonzero constant sectional curvature,
according to the theorem 3,
. If the
Riemannian manifold has a nonzero constant sectional curvature,
according to the theorem 3, 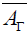 =
=  . It is obvious that this manifold has
a regular curvature.
. It is obvious that this manifold has
a regular curvature.
Remark 5: The result of the theorem 5 is not true in general if we only
impose the fields of projectable vectors to be those of Killing, that is to say
to belong to Ag without being elements of 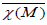 .
.
The elements of Ag even projectable form in general an algebra of infinite dimension.
Example 3
We assume 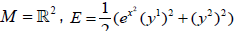 The spray S is written
The spray S is written
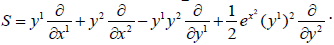
The nonzero coefficients of the connection are:
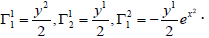
The horizontal vector fields are generated by
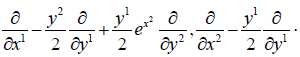
The curvature R is not zero. The elements of 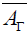 are
are
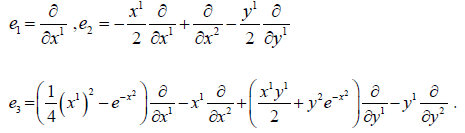
The Lie algebra  coincides with
coincides with  . It is semi-simple.
. It is semi-simple.
Example 4
We assume 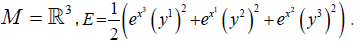
The spray is written:
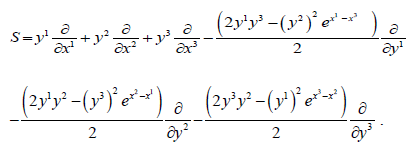
The coefficients of the connection are:
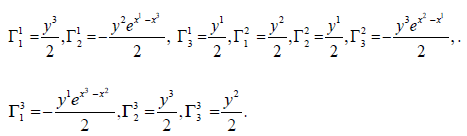
The Γ connection has a regular curvature. We note that  is
generated by
is
generated by 
According to this example, we note that the Lie algebra of Killing fields Ag even projectable is of infinite dimension.
Example 5
We take 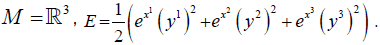
The spray S is written
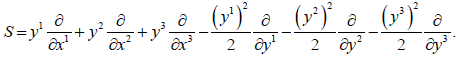
The non-zero coefficients of the connection are:
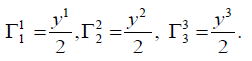
Horizontal fields are generated by
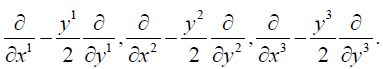
The curvature R is zero.
The elements of 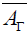 are generated by:
are generated by:
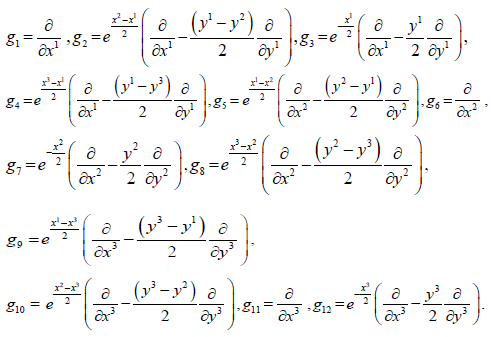
The horizontal vectors fields which form the commutative ideal are {g3,g7,g12}.
The elements in  , according to the proposition 19 (Table 1), are
, according to the proposition 19 (Table 1), are
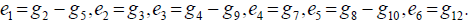

Table 1. Multiplication table of 
\We see that the derivative ideal from  coincides with
coincides with  .The commutative ideal is generated by {e2, e4, e6}.
.The commutative ideal is generated by {e2, e4, e6}.