Shear Stresses during the Flow of Structured Suspensions: Accounting for the Formation of Trimers

AI Levinsky^*
*Correspondence: Dr. AI Levinsky, Department of Mathematics, University of Applied Sciences, Hamburg, Germany, Email:

Keywords

Rheology • Suspensions • Flow curves

Introduction

An equation was derived based on the Krieger formula, generalized to multicomponent suspensions. A one-component suspension was considered as consisting of two fractions: single grains of the dispersed phase and their dimers, and equilibrium is established between them, which is linearly dependent on the shear rate [1]. It was shown that this equation describes well the flow of both dilatant and pseudoplastic suspensions. However, it was also shown there that the systems known from the literature, in which pseudoplastic behavior is replaced by dilatant behavior, are not described by the equation derived there [2]. At the same time, it was suggested that taking into account the formation of trimmers could also describe such systems.

The purpose of this work is to verify the above assumption, i.e. to expand the equations derived by taking into account the formation of trimmers and to investigate their parametric dependence are there such sets of parameters for which the curve of the dependence of the shear stress on the shear rate gets an inflection point, that is, becomes N-shaped and/or S-shaped.

So, Krieger's formula, generalized to the case of multicomponent suspensions, has the form [3]:

Where φ is the total volume fraction of all solid components, is the characteristic viscosity of the i-th component, and are its volume fraction and limiting concentration, respectively.

The generalized Krieger formula (1-2) can be used to describe the dependence of the shear stress τ on the shear rate, if we introduce assumptions similar to how it was done:

• One-component suspension can be considered as a system consisting of three fractions: single grains of the suspension, their dimers and trimers, whereby single grains, dimers and trimmers correspond to different values of the parameters and.

• The dimerization of single grains can be considered as a reaction with a rate constant the decay of dimers - as a reaction with a rate constant linearly dependent on the shear rate : similarly for the formation and decay of trimmers - and .

Thus, any shear rate corresponds to their equilibrium concentrations of single grains, dimers and trimers, from which, according to formulas (1-2), it is possible to calculate the viscosity. The latter is the coefficient of proportionality between the shear stress and the shear rate: where is the yield point.

Let there be n grains of the solid phase in a unit volume of the suspension, and let the average grain volume be v. Then the volume fraction v of the solid phase is.

At a given shear rate, equilibrium is established between single grains and dimers: with equilibrium constant.

Similarly, the reaction of formation of trimmers; its equilibrium constant. Multiplying the last equality by v (average grain volume) and introducing the notation i.e., we obtain a cubic equation for the equilibrium concentration of single grains; it was solved numerically by Newton's method. The coefficients of this equation, by virtue of (3) and (4), linearly depend on the shear rate:

The equilibrium concentrations of dimers and trimmers are calculated by the formulas and the shear stress-according to the generalized Krieger formula

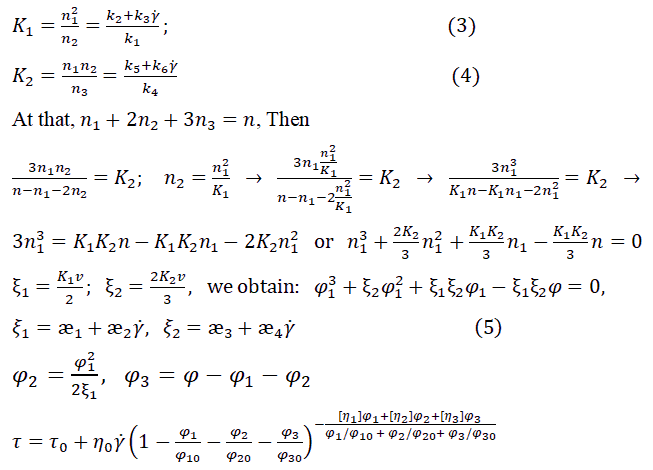
The form of the curve τ (γ) depends, therefore, on ten parameters:

• Characteristic viscosities

• Limiting concentrations

• Coefficients , expressing the dependence of the equilibrium constants on the shear rate, in accordance with formulas (5). The indicated parameters were varied in such a way that the curve

obtains an inflection point, i.e. takes an S- or N-shape. Such parameter sets have been found; two special cases are shown (Nshaped curve; corresponds to a system in which a pseudoplastic flow is replaced by a dilatant one) and (an S-shaped curve; corresponds to a system in which a dilatant flow is replaced by a pseudoplastic one) (Figures 1 and 2).

An approximation using the formulas derived here of real experimental data for latexes of a copolymer of styrene and ethyl acrylate, in which pseudoplastic behavior is replaced by dilatant behavior, although some discrepancies remain between experiment and theory [3-5], accounting for the formation of trimmers is consistent with experiment is much better than without such consideration (Figure 3).

Conclusion

Thus, taking into account the formation of trimmers makes it really possible to describe systems in which the nature of the flow changes with an increase in the shear rate (pseudoplastic is replaced by dilatant, or vice versa).

References

1. Yamauchi, Ryo, Koji Kato, and Yoshimitsu Ueno. "Formation Of Trimers Of Α-Tocopherol And Its Model Compound, 2, 2, 5, 7, 8-Pentamethylchroman-6-Ol, In Autoxidizing Methyl Linoleate." Lipids 23 (1988): 779-783.

   [Crossref] [Google Scholar] [Pubmed]

2. Copeland, Constance S, Robert W Doms, Eva M Bolzau, Robert G Webster, and Ari Helenius. "Assembly of Influenza Hemagglutinin Trimers And Its Role In Intracellular Transport." J Cell Biol 103 (1986): 1179-1191.

   [Crossref] [Google Scholar] [Pubmed]

3. McIntosh, Grant J. "Theoretical Investigations Into The Nucleation Of Silica Growth In Basic Solution Part I-Ab Initio Studies Of The Formation Of Trimers And Tetramers." Phys Chem Chem Phy 15 (2013): 3155-3172.

   [Crossref] [Google Scholar] [Indexing at]

4. Bayburt, Timothy H, Yelena V Grinkova, and Stephen G Sligar. "Assembly Of Single Bacteriorhodopsin Trimers In Bilayer Nanodiscs." Arch Biochem Biophy 450 (2006): 215-222.

   [Crossref] [Google Scholar] [Pubmed]

5. Bruch, Ludwig W, Wieland Schoellkopf, and J Peter Toennies. "The Formation Of Dimers And Trimers In Free Jet 4 He Cryogenic Expansions." J Chem Phy 117 (2002): 1544-1566.

   [Crossref] [Google Scholar] [Indexing at]