Specific Surface Area and Spring Lengths between Two Cubic Volumes Structure of the Activated Carbon Pellets, from Palm Leaves, Treated with KOH and Carbonized at Different Temperature

Fatima Musbah Abbas^1*, Abubaker Elsheikh Abdelrahman² and Abdul Kariem Arof^3
*Correspondence: Fatima Musbah Abbas, King Khalid University, Collage Science and Art, Dhahran Aljanoub, Abha, Saudi Arabia and Biotechnology and Genetic Engineering, National Center Researcher, Khartoum, Sudan, Email:

Keywords

Palm leaves • Activated carbon • Crystallite units • Spring length • Specific surface area

Introduction

Activated carbon is the collective name for a group of porous carbons manufactured to exhibit an extraordinarily large internal surface area and pore volume and size distribution. The unique characteristics of activated carbon are responsible for its adsorptive properties, which are exploited in many liquid-and gas-phase applications. The usefulness of activated carbon is due to increases in its applications such as removal of methylene from aqueous solution [1], adsorptions [2,3], water purification [4]. The activated carbons also have been evaluated as supercarpacitor [5]. A surface area is an important characteristic of activated carbon that greatly determines the properties and applications. Therefore, there are many carbonaceous materials that have been tested for a high surface area by KOH activations with bituminous coal of 3300 m²/g [6], grape seed of 1222 m²/g [7] and the oil palm leaves of 1685 m²/g [8].

Frequently, activated carbon is available in three main forms; these are powder, granular and pellet forms [9]. The pellet form is particularly useful because it is dense or contains particle sizes closed together in a solid manner [10]. In addition, the pellet form is required to characterize the physical, chemical and electrical properties [10,11]. The activated carbon prepared is either by treatment of a char with oxidizing gases, or carbonization of carbonaceous materials with simultaneous activation by a chemical, physical [10] or pressurized physical activation methods [12]. The crystalline structures of the carbon material have been used to describe the degree of graphitization based on an agreement of its interlayer spacing (d002) with that of pure graphite [13]. However, it has been reported that, with an increase in heat treatment temperature, the crystalline structure for the carbon becomes well arranged, the degree of graphitization increases and the interlayer spacing decreases [14-17]. Also it has been found that the porous properties of activated carbon produced decreased with increasing carbonization temperature [18,19]. Very often, the crystallite units and their statistical distribution play the fundamental role in describing the physical and mechanical properties, such as elastic medullas [14], thermal diffusivity [20] and surface area [21] of the carbon materials. A mathematical model has been proposed to estimate the elastic modulus based on crystallite units as a function of heat treatment temperature [14]. This mathematical model was further used to estimate the elastic modulus of the carbon pellets as a function of compression pressure [11,12]. Several attempts have been applied to improve the physical and mechanical properties, such as precarbonization process and self-adhesive properties [5,10], compression pressure [11].

In the present work, biomass palm leaves have been used as stating materiel to prepare activated carbon by KOH activation, due to a high carbon yield and low ash content. The palm leaves have been evaluated as an indicator of heavy metal atmospheric pollution in arid and semi-arid environments [22] and biomass carbon precursor for the activated carbon and carbon nanodots [11,12,23]. The crystallite units (Lc, La, and d002) were analyzed by X-ray diffraction and the specific surface area was estimated from crystallite unit Lc and the bulk density [12]. The specific surface was estimated using the mathematical model purposed by the Emmerich FG and CA Luengo [14] using the modification given in the present work. An ultrasonic technique was used to calculate the longitudinal velocity and the glassy carbon (Sigradur K) was used as a reference.

Materials and Methods

Sample preparation and measurements

Initially the raw palm leaves were held for 4 hours at 280°C in a vacuum chamber to cause them to shrink and break the palm leaves microstructure. The palm leaves after this had substantially the same shape, but with a greatly reduced weight of 34%, changed colors and reduced size casing to reduce bulk density. The pre-carbonized palm leaves was milled into a fine grain powder before being impregnated in KOH solution having a concentration of (0.0 - 0.07) by moles (M), with magnetic starrier for one untie mixed and kept for 16 hours, dried and converted into a pellets form by applying 12 metric tons of pressure. The carbonizations were performed using Vulcan Box Furnace (3-1750) equipment at different temperatures from 500°C to 1000°C in a nitrogen atmosphere using a multi-step heating profile schedule as following at 1oC/min from room temperature to 375oC of where it was held for 1 hour before heating was resumed at 3oC/min to (500- 800oC and then 5oC/min to 900-1000oC where it was finally held for 5 minutes at each carbonized temperature. After 5 minutes, the system was automatically allowed to cool down naturally to room temperature. The pellets produced were washed thoroughly with hot distilled water to remove the KOH contents and clean their surface until a pH of 5 and dried in an oven at 100°C for 4 hours (Figure 1). After removing of the KOH content, it will leave pores with a different pore size distribution in the final product. The diameter and thickness of the pellets were measured using a micrometer with six readings taken for each measurement and the average obtained. The bulk densities are determined by dividing their weight into volume (Figure 1).

The X-ray diffraction intensity of the carbon samples was measured using an X-ray diffractometer (Bruler Advanced Solution AXS D8), operating at 40 kV and 30 mA, using a Cu K X-ay radiations with a wavelength of 1.54 Å. The measurements of X-ray diffraction were taken for each sample, at diffraction angle of 2 over the ranges of 5oC – 60oC in steps size of 0.04oC. To characterize the crystallites units such as interlayer spacing (d₀₀₂), layer high (L_c) and layer diameter (L_a) of the graphitic like-crystallites from the reflection Bragg’s peaks intensity plan, a correction must be made so they have zero background line intensity and free from overlapping and instrumental broadening effects. The crystallite units of the activated carbon sample such as d002 spacing, layer diameter (L_a) and layer height (L_c) can be calculated from the full width at half maximum (FWHM) of the (002), (100) and (110) diffraction peaks intensity by Bragg’s and Deby-Sherrier equations using the Trace 1.4 X-ray diffraction program version 5 from Diffraction Technology PTG LTD, Australia to assess the accuracy. Trace 1.4 programs refines the intensity of each peak (as a separate variable) smooth the peak shape, as well as subtracts the background line and eliminates the K 2-peak from the diffraction intensity.

where θ is the scattering angle position, l is the wavelength of X-ray diffraction, K is a shape factor which is equal to 0.9 for L_c and 1.84 for L_a, β_c, a is the width of a reflection at half-height expressed in radians. For accurate measurement, the values of d₀₀₂ and La were fitted to the [24] expression (Equation 2), demonstrating the relationship between d₀₀₂ and L_a for the nongraphitic carbon as a single linear relation, given as:

The longitudinal velocity of the carbon pellets before and after carbonization was measured using the Ultrasonic Pulser-Receiver, Model 500 PR operated at 25 MHz at room temperature and the PICO instrument with the ADC-200 program. The pulsar section generated electric pulses that were converted into ultrasonic signals using matched transducers. Petroleum jelly was applied as a coupling medium at the probe-sample interface. A reference glassy carbon Sigradur-K (SIG-K) was used to calibrate the ultrasonic signal and measure the longitudinal velocity. The measurement of (SIG-K) agreed well with the value given by the supplier with an error of < 1%.

Mathematical Methods

Emmerich FG and CA Luengo [14] proposed a mathematical model to estimate the elastic modulus (E) of the carbon material from the crystallite units (L_c, L_a, and d₀₀₂) and volume fraction (X) as a function of their heat treatment temperature via the estimated diagram of a cubic granular volume structures (Figure 2) by assuming that the carbon granular structure to be mainly made of graphite-like microcrystalline, micropores and mesopores as:

The elastic modulus (E) in weakly attenuation materials can be given as [10].

Substitute equation (4) into equation (3) as:

Where

P = The bulk density

V = The longitudinal velocity

γ = Constant related to force and represents the degree of stiffness of the sample

L = The cube root of the mean granular volume structure, equal to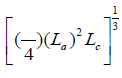

X = The volume fraction of the sample, can be given as: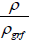

P_o = The bulk density of pure graphite (2.26 g m^-3)

n = Is an integer defines the order of change, given as:

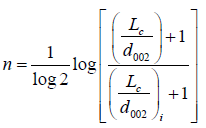
Where i is the initial value, in order to fit this model in our AC samples it is necessary to estimate the initial X-ray diffraction data, for the untreated AC pellets (0.0 M) has been used as an initial value in this work. By substituting the X value as:

Specific surface area (SSA)

The specific surface area (SSA) was estimated an empirically crystallite parameter (L_c) and the bulk density (ρ) using the equation (5) [16]

To estimate the specific surface area from the mathematical model [14] by substituting equation (7) into equation (4) to improve the accuracy of our measurements. Finally, Equation 13 is the second order polynomial equation by solving equation 10 to give two values ether – or +.

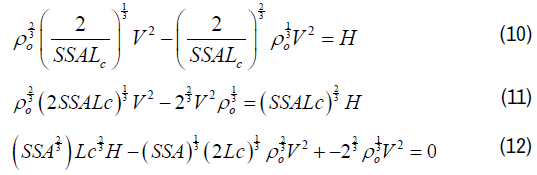
Spring length (SP)

The spring length is the distance between two cubic granular volume structures is given as [15].

Results and Discussion

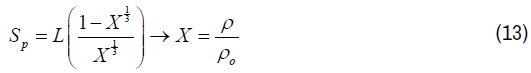
The carbonization process of untreated and treated grain pellets for sufficient time at an appropriate carbonization, a heat treatment temperature at (500ºC to 1000ºC). Showing a large weight losses and volume change occurred with the body physically shrinking to maintain its structural integrity [25]. This indicated that the grain pellets were subjected to compressive stresses during the heating process. Therefore, during the heating process, it is expected that the volume is reduced due to loss of adsorbed water and volume reduction due to release of tar and volatile compounds [26,27].

X-Ray diffraction

The XRD analysis found that the structure of all the carbon pellets produced is non-graphitic structure revealed by the higher background line intensity profiles [28]. Broad Bragg’s peaks were visible in the XRD spectrum of the all-carbon samples prepared from untreated and treated grain powder as shown in Figure 3. It shows that the diffraction intensity, initially at (002) and (100) Bragg's peaks, was broad, but as the carbonization temperature increased, the diffraction intensity sharpened at 1000oC carbonization temperature. The sharpened intensity profiles indicate that the CPs have a more crystalline structure, as the carbonization temperature increases up to 1000oC. Otherwise, it is due to reduction of the porous properties with increasing the carbonization temperature [18,19] (Figure 3).

Figure 4 represents the X-ray diffraction intensity for activated carbon pellets prepared at 1000oC for background and instrumental broadening and fitted into Gaussian distribution curves. Similar corrections were carried out to all of the diffraction intensities on the activated carbon pellets (Figure 4).

Figure 5 represents the variation of the interlayer spacing d₀₀₂ for the AC activated with KOH having a concentration of (0 – 0.07 M) plotted as a function of carbonization temperatures and tableted in Table 1. The results show that d₀₀₂ data decreased linearly with increasing the HTT and increased linearly with increasing the KOH concentration. Increases in the d002 may lead to reduction in crystalline structure by development of the pore structure and increasing surface roughness because of releasing the KOH molecules from the activated carbon pellets produced (Figure 6). While the decrease in the d₀₀₂ indicates that there is an improvement of the crystalline structure, to more as a graphite-like structure when the carbonization temperature increased from 500oC to 1000oC. A similar observation has been made on another carbon precursor cellulose with increasing temperature [15,21] (Table 1, Figures 5 and 6).

L_c and L_a were greatly increased with increasing carbonization temperatures as shown in Figure 7 and summarized in Table 1. Justifying that the system behaves more and more as a graphite-like structure with increasing carbonization temperatures. A similar observation on crystallite parameters was made on activated carbon from petroleum coke chemically activated with KOH [29]. The La obtained was close to those from other carbon materials prepared from polymeric carbon and petroleum coke annealed at different temperatures [29]. Increasing the carbonization temperature caused L_c and L_a to increase from 6.5 nm to 9.4 nm and from 9.9 nm to 31.4 nm respectively. These findings indicate that the samples acquired larger crystallite parameters at the higher temperature. It was also indicated that the crystallite units decreased with increasing molarities of KOH used (Figure 7).

The relationships between d₀₀₂ and La can be deduced by equation (2) that for large L_a the approaches zero and that d₀₀₂, vs. 1/La obey the linear equation as shown in Figure 8. The data fitted the data very well except the samples prepared at 500°C to 600°C (Equation 14). It could be their structure did not yet achieve the structure, with the constant equal to 9.44 and cut axis of 3.354 Å. However, at a higher carbonization temperature (d₀₀₂) becomes very depend on 1/L_a (Figure 8).

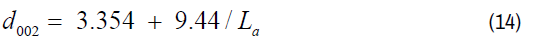
Specific surface area

The data in Table 2 represents the specific surface area (SSA) of the ACPs estimated from the bulk density and layer height (L_c) using Equation (9) and the specific surface area (SSA1) estimated by solving the polynomial Equation (12). The data shows that the specific surface area increased consistently with increasing KOH-concentration. It seems that activated carbon pellets have an excellent specific surface area of (1308.7-1658 m²/g), which is a range of the commercial activated carbon from coconut shell of (800 – 1500 m²/g) [30] and the oil palm leaves of 1685 m²/g [8].

The data show that a very good agreement between SSA and SSA1 by adjusting the value degree of stiffness (γ) of 0.14 for the ACP samples treated with 0.02 M, 0.06 M and 0.07 M KOH, while, the value of SSA is quite high compared to that of SSA1 for the ACP treated with 0.03 M, 0.04 M and 0.05 M KOH, indicate that there is an erroneous.

This implies that the KOH treatment can control the pore size of the CPs, with a high specific surface area achieved by low KOH concentration. Therefore, we consider that equation 12 is more accurate to be used to estimate the specific surface area, due to including the crystallite units (L_c, La and d₀₀₂), longitudinal velocity (V) and bulk density of the pure graphite (ρ_o), compared to that of equation (7) which contains only the bulk density (ρ) and layer height (L_c) of the samples. The above results confirm the validity of the mathematical model by Emmerich FG and CA Luengo [14] and the polynomial equation (10) given in this work for deriving specific surface area of the carbon pellets.

The microscopic structure of the carbon samples was assumed to be made of granular cubic. The predicted specific surface area SSA1 using the microscopic cross-linking model based on such an assumption was in good agreement with the SSA estimate of bulk density and layer height, making it suitable to be developed and used for estimating the surface area of the pore materials. Good prediction results of the specific surface area demonstrated the reliability of the model (Table 2).

Spring length

Table 3 and Figure 9 show the spring length between the cubic granular volume structures was decreased linearly with increasing KOH concentrations from 42.9 Å to 30.7 Å and such reduction on the spring lengths are probably due to the formulation of pores. However, that the ACPs pellets could only be stretched up to a certain point before cracking or deforming, when treated with a higher KOH concentration (Table 3 and Figure 9).

Conclusion

Analysis of X-ray diffraction profiles of the activated carbon pellets (ACPs) at different carbonization temperatures, at a higher carbonization temperature conferred greater order, which, in turn, resulted in the formation of a more graphite-like structure. In addition, the increases in L_c and L_a and decreasing d₀₀₂ in the ACPs produced, indicated that the system behaves more and more as a graphite-like structure with increasing temperature.

Based on the results, the mathematical model can be used to characterize the specific surface area and spring length between the two cubic volume granular structures of the activated carbon pellets, where it can identify the origins of microstructure in the carbon sample. The estimated specific surface areas (SSA and SSA1) are in good agreement and the spring length between two cubic volume structures was decreased with increasing KOH concentration. These results show that it is possible to combine the structural properties of a disordered or inhomogeneous material like carbon to perform such a characterization. Therefore, it can be concluded that the crystallite parameters can play a fundamental role in describing the physical properties of the ACPs produced.

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under grant number (GRP-323/43-1443) and Act centre for the great support.

Conflict of Interests

None.

References

1. El-Sayed, Gamal O., Mohamed M. Yehia and Amany A. Asaad. "Assessment of activated carbon prepared from corncob by chemical activation with phosphoric acid."Water Resour Ind 7 (2014): 66-75.

Google Scholar, Crossref, Indexed at

2. Islam, Md Azharul, I. A. W. Tan, A. Benhouria and M. Asif, et al. "Mesoporous and adsorptive properties of palm date seed activated carbon prepared via sequential hydrothermal carbonization and sodium hydroxide activation."J Chem Eng 270 (2015): 187-195.

Google Scholar, Crossref, Indexed at

3. Köseoğlu, Eda and Canan Akmil-Başar. "Preparation, structural evaluation and adsorptive properties of activated carbon from agricultural waste biomass."Adv Powder Technol26 (2015): 811-818.

Google Scholar, Crossref, Indexed at

4. Huang, Tingting, Rui Zhou, Jingqin Cui and Jin Zhang, et al. "Fast and cost-effective preparation of antimicrobial zinc oxide embedded in activated carbon composite for water purification applications."Mater Chem Phys 206 (2018): 124-129.

Google Scholar, Crossref, Indexed at

5. Taer, Erman, Nazilah Nikmatun, Rika Taslim and Ezri Hidayat. "The self-adhesive carbon powder based on coconut coir fiber as supercapacitor application." J Metastable Nanocryst Mater 33 (2021): 1-11.

Google Scholar, Crossref, Indexed at

6. Hsu, Li-Yeh and Hsisheng Teng. "Influence of different chemical reagents on the preparation of activated carbons from bituminous coal."Fuel Process Technol 64 (2000): 155-166.

Google Scholar, Crossref, Indexed at

7. Okman, Irem, Selhan Karagöz, Turgay Tay and Murat Erdem. "Activated carbons from grape seeds by chemical activation with potassium carbonate and potassium hydroxide."Appl Surf Sci 293 (2014): 138-142.

Google Scholar, Crossref, Indexed at

8. Chanpee, Sirayu, Napat Kaewtrakulchai, Narathon Khemasiri and Apiluck Eiad-Ua, et al. "Nanoporous carbon from oil palm leaves via hydrothermal carbonization-combined koh activation for paraquat removal."Molecules27 (2022): 5309.

Google Scholar, Crossref, Indexed at

9. Tadda, M. Abubakar, Amimul Ahsan, Abubakar Shitu and Moetaz ElSergany, et al. "A review on activated carbon: process, application and prospects."J Adv Civ Eng 2 (2016): 7-13.

Google Scholar, Indexed at

10. Deraman, M., Rahul Omar, Sarani Zakaria and Mardin Talib, et al. "Hardness and microstructure of carbon pellets from self‐adhesive pyropolymer prepared from acid and alkaline‐treated oil palm bunch."Adv Polym Technol23 (2004): 51-58.

Google Scholar, Crossref, Indexed at

11. Abdelrahman, Abubaker Elsheikh and Co-Author Dr Selma Elsheikh Abdelrahman. "Crystallites dimensions and electrical conductivity of Solid Carbon Pellets (SCPs) from date palm leaves (Phoenix dactylifera L.)."Acad J Res Sci Publ 4 (2023).

Google Scholar, Crossref, Indexed at

12. Yi, Hyeonseok, Koji Nakabayashi, Seong-Ho Yoon and Jin Miyawaki. "Pressurized physical activation: A simple production method for activated carbon with a highly developed pore structure."Carbon183 (2021): 735-742.

Google Scholar, Crossref, Indexed at

13. Kaburagi, Yutaka, Kohtarou Hosoya, Akira Yoshida and Yoshihiro Hishiyama. "Thin graphite skin on glass-like carbon fiber prepared at high temperature from cellulose fiber."Carbon 43 (2005): 2817-2819.

Google Scholar, Crossref, Indexed at

14. Emmerich, F. G. and C. A. Luengo. "Young's modulus of heat-treated carbons: A theory for nongraphitizing carbons."Carbon31 (1993): 333-339.

Google Scholar, Crossref, Indexed at

15. Dobiášová, L., V. Starý, P. Glogar and V. Valvoda. "Analysis of carbon fibers and carbon composites by asymmetric X-ray diffraction technique."Carbon37 (1999): 421-425.

Google Scholar, Crossref, Indexed at

16. Laszlo, Krisztina, Attila Bota and Imre Dékány. "Effect of heat treatment on synthetic carbon precursors."Carbon41 (2003): 1205-1214.

Google Scholar, Crossref, Indexed at

17. Aso, Hiromi, Koichi Matsuoka, Atul Sharma and Akira Tomita. "Structural analysis of PVC and PFA carbons prepared at 500–1000 C based on elemental composition, XRD, and HRTEM."Carbon42 (2004): 2963-2973.

Google Scholar, Crossref, Indexed at

18. Daud, Wan Mohd Ashri Wan, Wan Shabuddin Wan Ali and Mohd Zaki Sulaiman. "The effects of carbonization temperature on pore development in palm-shell-based activated carbon."Carbon38 (2000): 1925-1932.

Google Scholar, Crossref, Indexed at

19. Wang, Cui, Linfeng Li, Jinwen Shi and Hui Jin. "Biochar production by coconut shell gasification in supercritical water and evolution of its porous structure."J Anal Appl Pyrolysis 156 (2021): 105151.

Google Scholar, Crossref, Indexed at

20. Abubaker, E.A. "Physical and electrical properties of carbon pellets from cotton cellulose." Thesis (2006).
21. Arof, Abdul Kariem, M. Z. Kufian, M. F. Syukur and M. F. Aziz, et al. "Electrical double layer capacitor using poly (methyl methacrylate)–C4BO8Li gel polymer electrolyte and carbonaceous material from shells of mata kucing (Dimocarpus longan) fruit."Electrochim Acta 74 (2012): 39-45.

Google Scholar, Crossref

22. Al-Khashman, Omar Ali, H. Ala’a and Khalid A. Ibrahim. "Date palm (Phoenix dactylifera L.) leaves as biomonitors of atmospheric metal pollution in arid and semi-arid environments."Environ Pollut159 (2011): 1635-1640.

Google Scholar, Crossref, Indexed at

23. Fatima M. A., Zehhba A. A., Rehab O. E. and Abubaker E. A. "Characterization of pores size, surface area and fractal dimensions of activated carbon powder prepared from date palm leaves." Mol Bio 11 (2022b): 352.
24. Richards, B. P. "Relationships between interlayer spacing, stacking order and crystallinity in carbon materials."J Appl Crystallogr 1 (1968): 35-48.

Google Scholar, Crossref, Indexed at

25. Dhyani, Vaibhav and Thallada Bhaskar. "A comprehensive review on the pyrolysis of lignocellulosic biomass."Renew Energ 129 (2018): 695-716.

Google Scholar, Crossref, Indexed at

26. González-García, P. "Activated carbon from lignocellulosics precursors: A review of the synthesis methods, characterization techniques and applications."Renewable Sustainable Energy Rev82 (2018): 1393-1414.

Google Scholar, Crossref, Indexed at

27. Fermanelli, Carla S., Agostina Córdoba, Liliana B. Pierella and Clara Saux. "Pyrolysis and copyrolysis of three lignocellulosic biomass residues from the agro-food industry: A comparative study." J Waste Manag102 (2020): 362-370.

Google Scholar, Crossref, Indexed at

28. Yakout, S. M. and G. Sharaf El-Deen. "Characterization of activated carbon prepared by phosphoric acid activation of olive stones."Arab J Chem 9 (2016): S1155-S1162.

Google Scholar, Crossref, Indexed at

29. Chunlan, Lu, Xu Shaoping, Gan Yixiong and Liu Shuqin, et al. "Effect of pre-carbonization of petroleum cokes on chemical activation process with KOH."Carbon43 (2005): 2295-2301.

Google Scholar, Crossref, Indexed at

30. Hu, Zhonghua and M. P. Srinivasan. "Preparation of high-surface-area activated carbons from coconut shell."Microporous Mesoporous Mater 27 (1999): 11-18.

Google Scholar, Crossref, Indexed at

31. Kim, Myung Il, Chang Hun Yun, Young Jeon Kim and Chong Rae Park, et al. "Changes in pore properties of phenol formaldehyde-based carbon with carbonization and oxidation conditions."Carbon40 (2002): 2003-2012.

Google Scholar, Crossref, Indexed at