Research - (2020) Volume 9, Issue 3
Received: 17-May-2020
Published:
25-May-2020
, DOI: 10.37421/2168-9679.2020.9.450
Citation: Mohamed Moktar Chaffar. Star with Coefficient a in the set of Real Numbers. J Appl Computat Math 9 (2020) doi: 10.37421/
jacm.2020.9.450
Copyright: © 2020 Chaffar MM. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This paper gives two definitions: Star with coefficient a real and Star System with coefficient α in five unknowns. Examples of Star-System and Star-set are given, a relationship between two star-Systems is noted, and some general theorems are proven.
System equation • Agebra • Linear equations • Matrix matrices
The aim of the present paper is to introduce and study a system of five equations in five unknowns, that will be called Star-System with coefficient α in five unknowns. Let a, b, c, d, e, α be elements of a R, and let T1, T2, T3, T4, T5 be unknowns (also called variables or indeterminates). Consider a star with α coefficient (-- 1)
In addition to having the sum α in each line. The scalars α are called the star coefficient if α is a solution of equation α = T1(α) + T2(α) + T3(α) + T4(α) + T5(α) (Noted by α?), a vector (T1 , T2 , T3 , T4 , T5) is called a solution vector of this Star-System with coefficient α in five unknowns.
The present paper is organized as follows: In Section 2, we present some preliminary results and notations that will be useful in the sequel. In Section 3, we present some examples of Star-element. Section 4 is devoted to introduce and study a Star-function. In Section 5, we present one example of equivalent star-systems. Finally, in Section 6, we introduce the star-Differential operator and study some of their applications.
In this section, we introduce some notations and star-system with coefficient α defined.
Star with coefficient α in the set of real numbers.
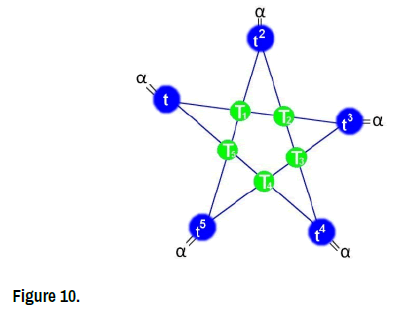
Definition 1. A star with α coefficient is composed of five numbers outside a, b, c, d, e and five numbers inside T1, T2, T3, T4, T5, These last five numbers are written in the form of 5-tuple (T1, T2, T3, T4, T5) (Figure 2).
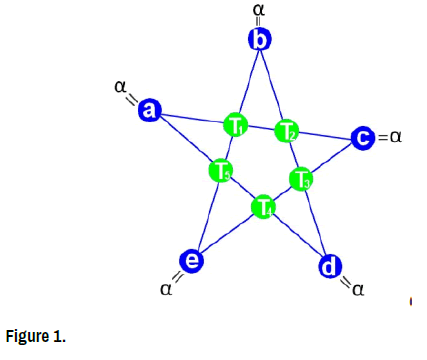
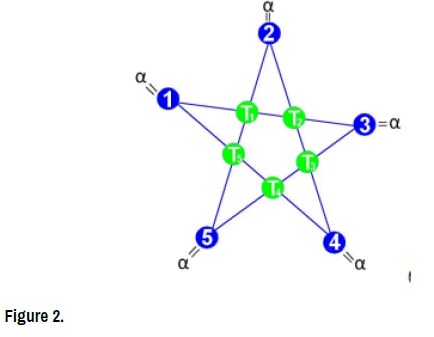
In addition to having the sum α in each line.
A star-system with coefficient α:
Definition 2. Let a, b, c, d, e and α be real numbers, and let T1, T2, T3 , T4 , T5 be unknowns (also called variables or indeterminates). Then a system of the form is called a star-system with coefficient α in five unknowns. We have also noted  [a,b,c,d,e;α] = α. The scalars a, b, c, d, e are called the coefficients of the unknowns, and α is called the constant ”Chaff” of the star-system in five unknowns. A vector (T1,T2,T3,T4,T5) in R5 is called a star-solution vector of this star-system if and only if
[a,b,c,d,e;α] = α. The scalars a, b, c, d, e are called the coefficients of the unknowns, and α is called the constant ”Chaff” of the star-system in five unknowns. A vector (T1,T2,T3,T4,T5) in R5 is called a star-solution vector of this star-system if and only if  [a,b,c,d,e;α] = α.
[a,b,c,d,e;α] = α.
The solution of a Star-system is the set of values for T1, T2, T3, T4 and T5 that satisfies five equations simultaneously.
A star-element: A star-element is a term of the five-tuple (T1, T2, T3, T4, T5) solution of a star-system  [a,b,c,d,e;α] = α, where (T1, T2, T3, T4, T5)∈ R5.
[a,b,c,d,e;α] = α, where (T1, T2, T3, T4, T5)∈ R5.
Star-Coefficient or Constant ”Chaff”: The star-Coefficient or Constant ”Chaff” is also noted by α? and is a solution of equation  = T1(α) + T0 2α) + T3(α) + T4(α) + T5(α), wher (T1 , T2 , T3 , T4 , T5) is solution of a star-system
= T1(α) + T0 2α) + T3(α) + T4(α) + T5(α), wher (T1 , T2 , T3 , T4 , T5) is solution of a star-system  [a,b,c,d,e;α] = α.
[a,b,c,d,e;α] = α.
Star-Matrix: The star-system with coefficient α can be written in matrix form

M* or MStaris called the star-Matrix of the star-system with coefficient α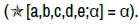
 a matrix is said to be of dimension 5 × 5. A value called the determinant of M
a matrix is said to be of dimension 5 × 5. A value called the determinant of M  , that we denote by |MStaris| or |M
, that we denote by |MStaris| or |M |, corresponds to square matrix MF. Consequently, the determinant of M
|, corresponds to square matrix MF. Consequently, the determinant of M is |M
is |M | = 1.
| = 1.
Set-Star: The set-star is constructed from the solution set of linear starsystem with coefficient α ( [a,b,c,d,e;α] = α). The Set-star will be noted by 
Star-System equivalent: Equivalent Star-Systems are those systems having exactly same solution, i.e. Two star-systems are equivalent if solution of on starsystem is the solution of other, and vice-versa.
Parametrized Curves: A parametrized differentiable curve is simply a specific subset of R5 with which certain aspects of differntial calculus can be applied.
Definition 3. A parametrized differentiable curve is a differentiable map α : I →R5 of an open interval I = (a,b) of the real line R in to R5
Regular Curves: A parametrized differentiable curve α : I →R5, We call any point that satisfies α’(t) = 0 a singular point and we will ristrict our study to curves without singular points.
Definition 4. A parametrized differentiable curve is a differentiable α : I → R5 is said to be regular if α’(t) ≠ 0 for all t ∈ I
Parametric Arclength: Generalized, a parametric arclength starts with a parametric curve in R5. This is given by some parametric equations T1(t),T2(t),T3(t),T4(t),T5(t) , where the parameter t ranges over some given interval. The following formula computes the length of the arc between two points a, b.
Lemma 1. Consider a parametric curveT1(t),T2(t),T3(t),T4(t),T5(t), where t ∈ (a,b). The length of the arc traced by the curve as t ranges overt (a,b) is
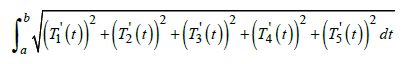
Thereafter I start with several examples with detailed solutions are presented.
This section will deal with solving problems with star-systems of five linear equations and five variables.
Example 1. A linear star-system with coefficient α composed of five linear equations in five variables T1 , T2 , T3 , T4 and T5 has the general form  [a,b,c,d,e;α] = α. In example 1: (a,b,c,d,e) = (1,2,3,4,5) When looking for the Solution of StarSystem with coefficient
[a,b,c,d,e;α] = α. In example 1: (a,b,c,d,e) = (1,2,3,4,5) When looking for the Solution of StarSystem with coefficient  [1,2,3,4,5;α] = α of Linear Equations, we can easily solve this using Star-Matrix
[1,2,3,4,5;α] = α of Linear Equations, we can easily solve this using Star-Matrix 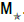 .
.
the star-systems of Linear Equations 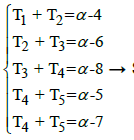 So the overall solution
So the overall solution
is the set-star: 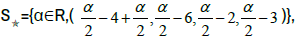
in a particular case if 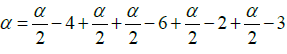 that is to say α=10
that is to say α=10
We obtain the following results:
• The Star-coefficient: 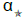 = 10
= 10
• The star-element is (1,5,−1,3,2) (Figure 3)
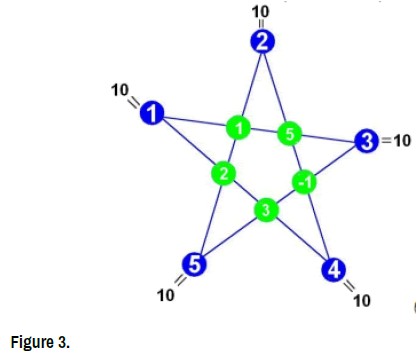
Note 1. It is important to mention that a solution is made up of five values, (T1 , T2 , T3 , T4 , T5). A solution is made up of the set of values jointly taken by the variables to satisfy the system’s equations.
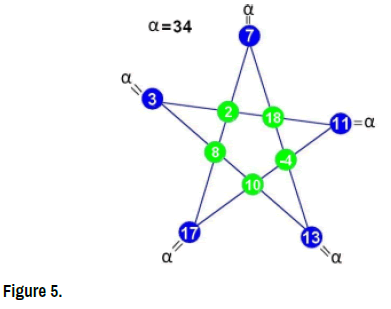
Example 2. ”Image of a five prime numbers”
Solve the following Star-system with coefficient α and five unknowns:
 [3,7,11,13,17;α] = α. (Figure 4)
[3,7,11,13,17;α] = α. (Figure 4)
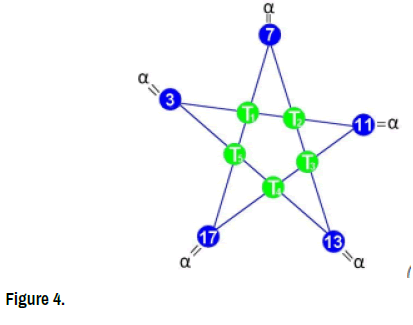

System  [3,7,11,13,17;α] = α is therefore
[3,7,11,13,17;α] = α is therefore
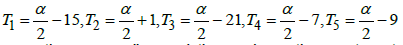
So the overall solution is the star-set: S =
= 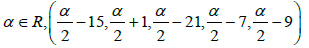 in a particular case if
in a particular case if 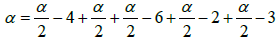 Then
Then
• The Star-coefficient:  = 34
= 34
• The star-element is (2,18,−4,10,8) (Figure 5)
More generally
Theorem 1. Let α ∈R, for all (a,b,c,d,e) ∈R5 the star-system [a,b,c,d,e;α] = α has a unique solution 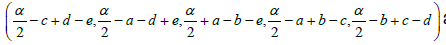 and the star-system we have unique star-cofficient:
and the star-system we have unique star-cofficient:  = 2/3(a+b+c+d+e)
= 2/3(a+b+c+d+e)
For any star-system  [a,b,c,d,e;α] = α, the star-element is
[a,b,c,d,e;α] = α, the star-element is 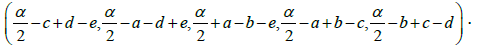
If 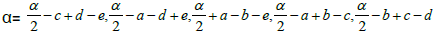
Then
• The Star-coefficient: 

In the following theorem, we give some useful result. Theorem 2: Let α ∈ R, for all t ∈ R the Star-system  [t,t,t,t,t;α] = α has a unique solution, the Star-set containing only the vector (
[t,t,t,t,t;α] = α has a unique solution, the Star-set containing only the vector (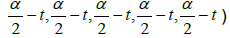 and the Star-system we have unique starcoefficient
and the Star-system we have unique starcoefficient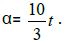
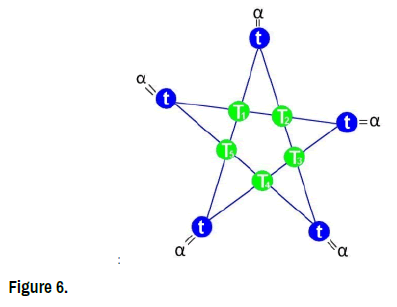
Proof theorem (Figure 6)
The star with coefficient α:
Consider the following star-system of 5 equations in 5 unknowns:
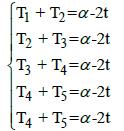
So the overall solution is the Star-set: S =
= 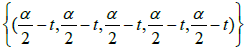
in a particular case if 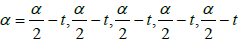 Then
Then
• The Star-coefficient: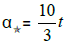
• The star-function:  (Figure 7)
(Figure 7)
Theorem 3: Let α ∈ R, for all t ∈ R the Star-system 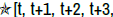
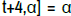 has a unique solution, the Star-set containing only the vector (
has a unique solution, the Star-set containing only the vector (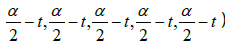 and the Star-system we have unique starcoefficient :
and the Star-system we have unique starcoefficient :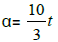
Proof theorem (Figure 8)
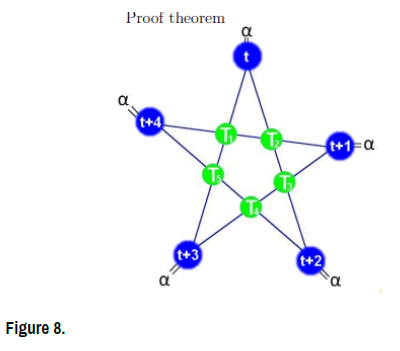
Consider the following star-system of 5 equations in 5 unknowns:
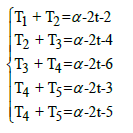
So the overall solution is the Star-set: 
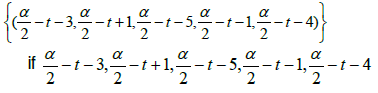
Then
• The Star-coefficient: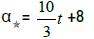
• The star-function: 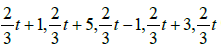 (Figure 9)
(Figure 9)
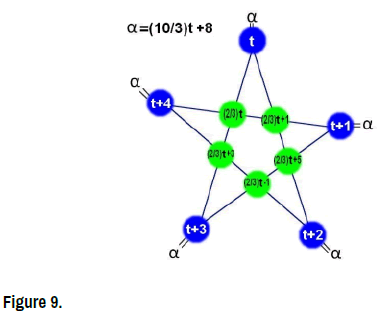
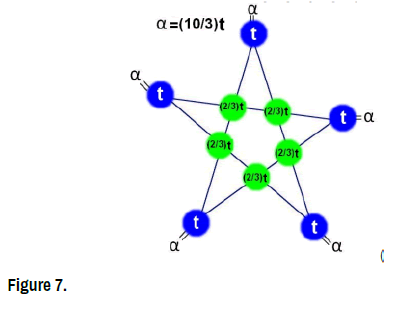
Theorem 4: Let α ∈ R, for all t ∈ R the Star-system  [x,2x, 3x, 4x, 5x, α] = α has a unique solution, the Star-set containing only the vector (
[x,2x, 3x, 4x, 5x, α] = α has a unique solution, the Star-set containing only the vector (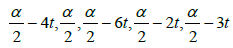 ) and the Star-system we have unique star-coefficient : α= 10t .
) and the Star-system we have unique star-coefficient : α= 10t .
Proof theorem (Figure 10)
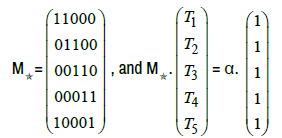
So the overall solution is the Star-set: 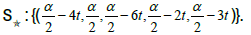
if 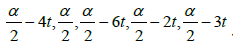 Then
Then
• The Star-coefficient:  = 10t.
= 10t.
• The star-function: (t,5t,−t,3t,2t) (Figure 11)
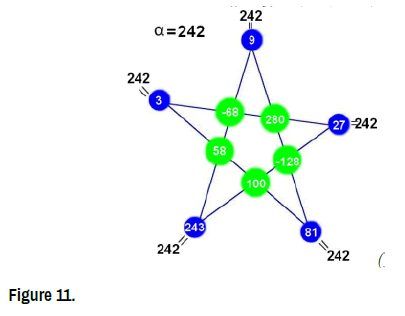
In the special case t=3
•The Constant ”Chaff”: α = 30
•The Star-set: 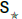 = {3,15,−3,9,6)}. (Figure 12)
= {3,15,−3,9,6)}. (Figure 12)
Theorem 5: Let α ∈ R, for all t ∈ R the Starsystem  [t,t2, t3, t4, t5,α] = α has a unique solution,
[t,t2, t3, t4, t5,α] = α has a unique solution, 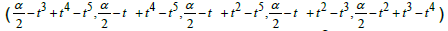 and the Star-system we have unique star-coefficient
and the Star-system we have unique star-coefficient 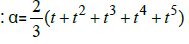
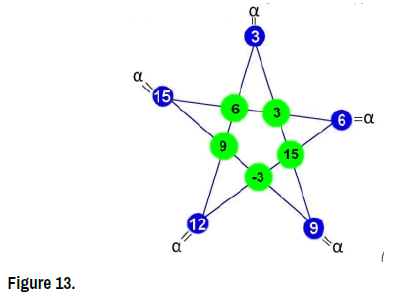
Proof theorem (Figure 13)

Star-set: 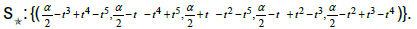
If 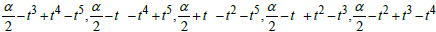
Then
• The Star-coefficient: 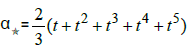
• The star-function:  defined by:
defined by:
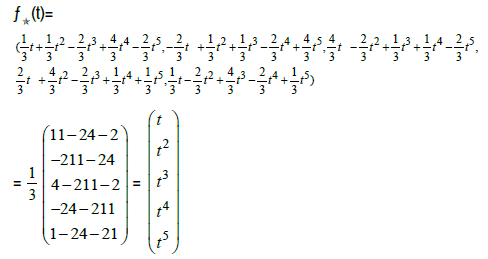
In the special case t=3
• The Star-coefficient: α = 242
• The Star-set:S = {(−68,280,−128,100,58)}.(Figure 14)
= {(−68,280,−128,100,58)}.(Figure 14)
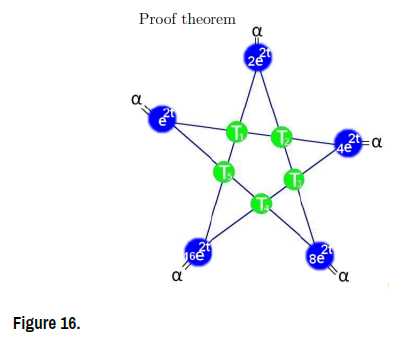
Theorem 6: Let α ∈R, for all t ∈R the Star-system 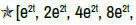
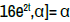 has a unique solution
has a unique solution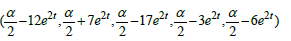 and the Star-system we have unique star-coefficient:
and the Star-system we have unique star-coefficient:
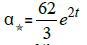
Proof theorem (Figure 15)
Consider the following star-system of 5 equations in 5 unknowns:
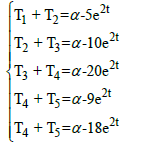
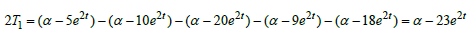
So the overall solution is the Star-set: S =
=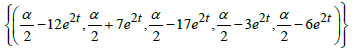
If α =T1 + T2 + T3 + T4 + T5 then the star coefficient: 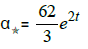
Let’s find the length of 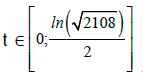 of the star-function ƒ(t)=
of the star-function ƒ(t)= 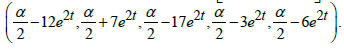 We compute
We compute 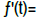
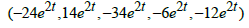 and
and
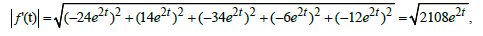
So the length is 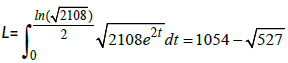
In the special case x= 0
• The star coefficient: 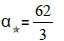
• The Star-set: 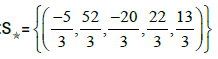
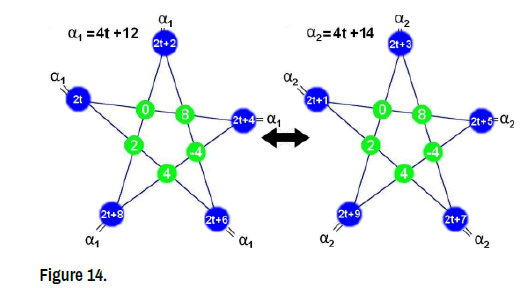
Theorem 7.
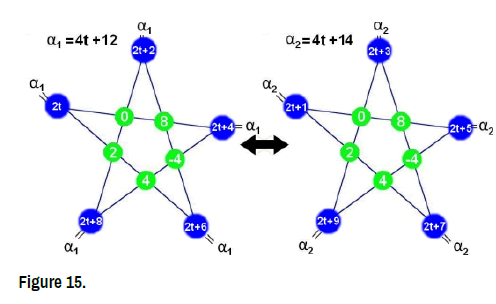
For all t ∈R if α1 = 4t + 12 and α2 = 4t + 12 then the two star-systems :  1[2t,2t+2,2t+4,2t+6,2t+8;α1] = α1 and
1[2t,2t+2,2t+4,2t+6,2t+8;α1] = α1 and  2[2t+1,2t+3,2t+5,2t+7,2t+9;α2] = α2 are equivalent.
2[2t+1,2t+3,2t+5,2t+7,2t+9;α2] = α2 are equivalent.
Proof theorem
The star-system 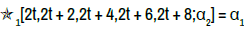 can be written as:
can be written as:
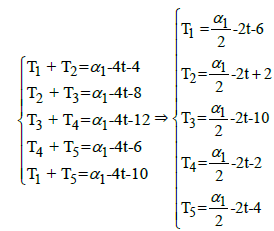
The star-system 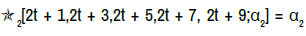 can be written as:
can be written as:
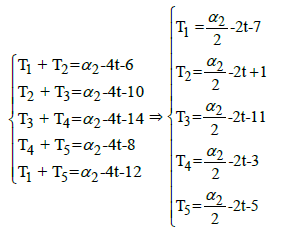
For all t ∈ R, if the tow Constants of the two star-systems α1 = 4t +12 and 2 α = 4t+14 then the Star-set of the two star-systems: 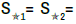 {(0,8,-4,4,2)} (Figure 16)
{(0,8,-4,4,2)} (Figure 16)
New Star-Differential operators: During our study of the construction of star-system, some new star-differential operators are required to be introduced.
Theorem 8. Let α ∈R, for all t ∈R and for all f be an n-times differentiable real function defined in interval I of R, the Star-system 
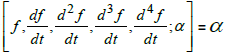 has a unique solution and the Star-system we have unique star coefficient:
has a unique solution and the Star-system we have unique star coefficient: 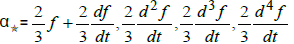
Notation: A variety of notations are used to denote the n-times derivative.
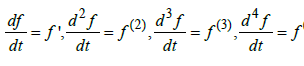 (4)
(4)
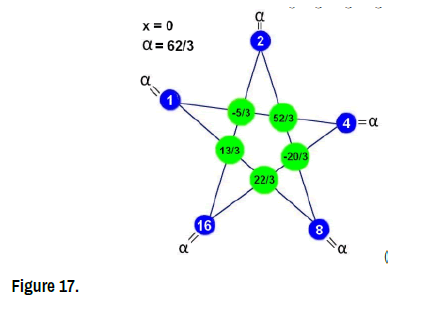
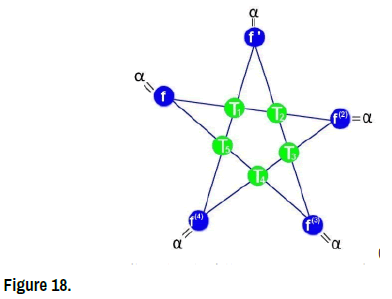
Proof theorem (Figure 17)
Consider the following star-system of 5 equations in 5 unknowns:
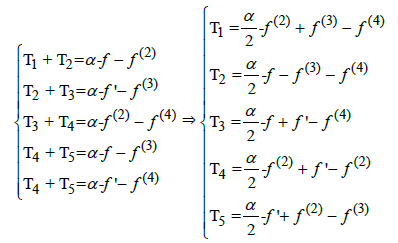
If 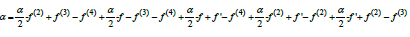 then the star coefficient:
then the star coefficient: 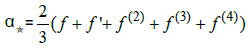
In the special case 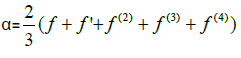

f(t)=sin(t): f is n-times differentiable at all t ∈R
For all t ∈R the star-system  [sint,cost,−sint,−cost,sint;α] = α
[sint,cost,−sint,−cost,sint;α] = α

• The Star-Set: 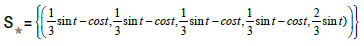 (Figure 18)
(Figure 18)
f(t)=cos(t): f is n-times differentiable at all t ∈R
For all t ∈R the star-system  [cost,−sint,−cost,sint,cost;α] = α
[cost,−sint,−cost,sint,cost;α] = α

So the solution set is The Star-Set: 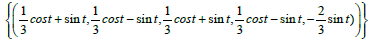
The star-function 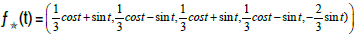 defined in R to R5
defined in R to R5
It’s not possible to draw a 5D graphic, but in another world, a 5D world, it would be.
which can be written
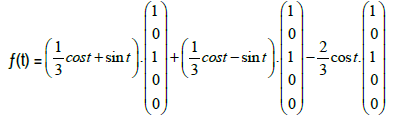
The three vectors shown span the solution star-set. it is also not too hard to prove that they are linearly independent; therefore they form a basis for the solution starset (Figure 17).
In an abstract setting we can generally say that a projection is a mapping of a set, which means that a projection is equal to its composition with itself. (Figure 18)
in our case, we define by
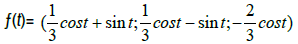 the Star function in R to R3.
the Star function in R to R3.
In our world this Star-function is represent by (Figure 19):
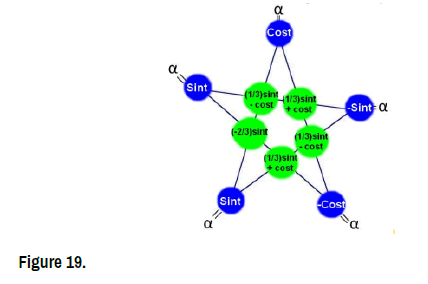
f(t)=sin(2t): f is n-times differentiable at all t ∈R For all
t ∈R the star-system [sin2t,2cos2t,−4sin2t,−8cos2t,16sin2t;α] = α
• The star coefficient: α = 2 3 (14sin(2t)−6cos2t) (Figure 20)
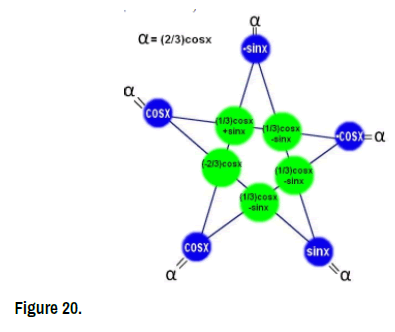
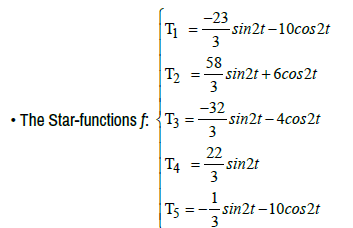
f(t)= et: f is n-times differentiable at all t ∈R (Figure 21)
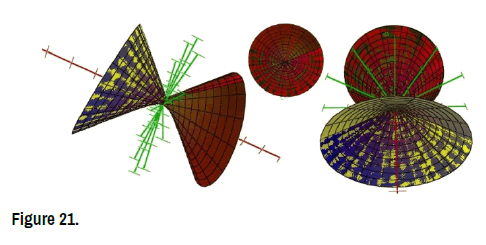
For all t ∈R the star-system [et, et, et, et, et;α] = α

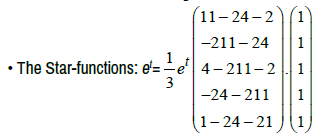
Journal of Applied & Computational Mathematics received 1282 citations as per Google Scholar report