Research - (2021) Volume 10, Issue 4
Received: 25-Feb-2021
Published:
22-Apr-2021
, DOI: 10.37421/2168-9768.2021.10.262
Citation: Fikadu Kinfe, Getachew Gedefaw, Moges Ademe. "Study of Design Rainfall for the case of Beles Sugar Development Project Irrigation Command Area." Irrigat Drainage Sys Eng 10 (2021): 262.
Copyright: © 2021 Kinfe F, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Drainage problem in Beles Sugar Project is becoming severe during rainfall season that the effective rainfall was greater than the sugarcane water requirement and higher area coverage of vertisols. To remove this excess rainfall through installations of surface drainage system, this study was conducted to estimate design rainfall in magnitude and recurrence interval based on the recorded maximum rainfall. The independent, homogeneity, and outliers of the recorded data were tested accordingly. Probability of exceedence and return periods for daily maximum rainfall was determined using Kimball’s method. Gumbels method was used to compute design rainfall of different desired return period. The relation between observed and computed data was undertaken using regression function. Thus, recorded rainfall data was independent and homogenous at 5% signifance level. Also there was no value greater than the high outliers (151.3 mm) and no value less than the low outliers (41.0 mm).The lowest maximum rainfall (48.6 mm) had a probability of 96 .9% which likely to occur every one year. The highest maximum rainfall (150.1 mm) had a probability of 3 .1% which likely to occur three times in every 100 years period. Within the same 10 years return period, the computed design rainfall (114.7 mm) was deviate by 0.04 with the observed rainfall (110.3 mm).The average deviation of observed and computed rainfall data from its trend line function were 0.004 and 0.002 respectively. The correlation between observed and computed rainfall of trend line function was 0.98, thus it was highly correlated and the perfect reality. Design rainfall for 10 years return period (110.3 mm) was suggested for estimation of Beles Sugarcane open earth drainage channels. Thus, the Project Engineers and Hydrologists has to considered this study pre-requisite for planning, design and management of hydrological, hydraulic, drainage structures, barrages, dams, spillways, bridges, culverts and so on that have been executed in the Project.
Waterlogging • Excess rainfall • Probability of exceedence • Desired return period • Design rainfall • Drainage channels
Drainage problem in Beles Sugar Development Project is becoming severe during rainfall season. The problem is mostly existed in black clay soil of sugarcane fields which are designed for overhead sprinkler irrigation system. As per stated in the study [1] and with current filed visual observation, most of this soil portion of the sugarcane command areas were challenged with water ponding problem. The majority of the irrigation command area at Upper Ayma and Beles are waterlogged throughout the rainy season from the higher area coverage of vertisols and other soil units both due to external (surface) and internal drainage problems [2].
According to sugarcane water requirement in rainy season from June to September is much less than effective rainfall. The cane has stunted growth and poor performance in the water ponding affected areas and also the agricultural operations like cane harvesting, timely tillage, and planting activities are difficult to execute due to this problem and future land productivity is under question. Thus, it is important to remove this excess rainfall from the sugarcane field by installing surface drainage system in this area of the Project.
Considering this, the Project has given attention to remove this excess rainfall from the sugarcane fields. Having this, initial surface drainage works has been started in some fields. But, there is a data limitation on design rainfall intensity for determining the rainfall-runoff relationship. In order to design drainage system based on the existing condition of command area, knowing the relationship between this excess rain and runoff is very crucial and a mandate. It needs to study design rainfall intensity for different recurrence years to estimation peak runoff occurred from excess rainfall. This means hydrological and drainage structures must be constructed with this fact taken into consideration [3]. To better explain the statistical nature of storm frequency, study the percentage of a particular storm event being exceeded in any one-year probability is important [4].
In the planning and design of water resources projects, engineers and planners are often interested to determine the magnitude and frequency of floods that will occur at the project areas. Estimation of peak flood flow rate for a desired return period is a pre-requisite for planning, design and management of hydrological, hydraulic, drainage structures, barrages, dams, spillways, bridges, culverts and so on. Design rainfall intensity is significant to estimate peak runoff for the design of these stated structures.
Frequency analysis is one of the main techniques used to define the relationship between the magnitude of an event and the frequency with which that event is exceeded. The availability of data is an important aspect in frequency analysis. Rainfall Intensity duration frequency curve was developed earlier in Amahara Regional based. This study was not area specific and not yet developed specifically for the Beles Project Sugarcane Command area. Design rainfall for nineteen years and only for ten years return period was also estimated according to [5]. This study used limited available data from the year 1987 to 2005G.C and it wasn’t consider different return periods especially for large recurrence periods. Minimum of thirty years data is commonly used and adequate for design of hydrological and drainage structures. Currently the study area has thirty one years available data starting from 1987 G.C till now.
The larger the database, the more accurate the estimates will be. From a statistical point of view, estimation from small samples may give unreasonable or physically unrealistic parameter estimates. In practice, however, data may be adequate, limited or in some cases may not be available for a site. For the safe design of structures even a 50-year or 100-year precipitation may be inadequate due to the unusual meteorological combinations resulting in very high precipitation. It has its own limitation on engineers design decision to undertake different options such as in terms of size, cost and so on.
Therefore, this study was initiated to develop design rainfall in magnitude and different recurrence interval based on the available years and those recurrence years which haven’t available data. Thus, the Project Engineers and Hydrologists can consider and access this data pre-requisite for planning, design and management of hydrological, hydraulic, drainage structures, barrages, dams, spillways, bridges, culverts and so on. The general objective of this work was to study design rainfall for the case of Beles Project Sugarcane Command areas which is an input for determination of design flow rate that occurred from excess rainfall. The specific objectives were;
➢ To study the probability of exceedance and return periods of observed rainfall in the Project command area
➢ To study design rainfall for different recurrence periods using Gumbel method and to suggest design rainfall intensity with different desired return periods.
Description of the study area
Beles Sugar Development Project is located in Jawi Woreda, which is 162 km far from the western periphery of Amhara National Regional State, Bahir Dar town. The project has two sugarcane command area which are Upper Beles and Upper Ayma. Upper Beles Right side irrigation command area is located from 0202452 to 0247992 m East and 1237727 to 11290353 m North UTM, whereas the Upper Ayma irrigation command area is situated between 0198473m to 0225347m East and 1277734 m to 1308983 m North UTM. Upper Beles and Ayma cover 37,207 ha and 35,737 ha respectively. The command areas have low to medium elevation differences with an altitude range of 806 to 1242 meters above sea level [6]. According to Figure 1 delineated map, the project command areas were located close to Pawe station, which are 3 and 26 km from the boundary of Upper Beles and Ayma command area respectively. The mean annual rainfall about the irrigation command area was represented by Pawe Station with mean annual rainfall of 1593 mm (from 1998-2015). The highest and lowest daily maximum rainfall (from 1987-2017) of the command area was 150.1 and 48.6 mm respectively which were represented by Pawe Station. The average daily maximum rainfall of these respective years was 81.3 mm. The location map of the study command area was shown in Figure 1 below.
Data collection
The irrigation command area was represented by Pawe and Beles/Jawi Metrological Station. Considering a minimum of thirty years daily maximum rainfall data for design of hydrological, drainage and others huge irrigation and flood structures is adequate. But, Jawi/Beles Metrological station had data only for 6 years. Thus, Pawe Station was used to represent the command area. The daily maximum rainfall data was collected for thirty one years from the Pawestation. Non spatial map of the project command area which was in pdf format was collected from the feasibility design study document to delineate the irrigation command area map for location and spatial coordination. GPS data of Jawi and Paw metrological Station were collected to determine the spatial location between the Stations and command area. Others documents related to this study were referred and taken under consideration.
Data quality analysis
The independent, homogeneity, and outliers quality test of rainfall data recorded from the year 1987 to 2017 was checked accordingly.
Test for independence and stationarity
The independence of maximum daily rainfall data recorded for each year (1987-2017) within the station was analyzed using (Wald-Wolfowitz, 1943 as cited in Ramachandra, 2009) test by comparing the static data set value (u) with the standard normal variate uα/2 corresponding to probability of exceednce ∂/2(5% significant level).
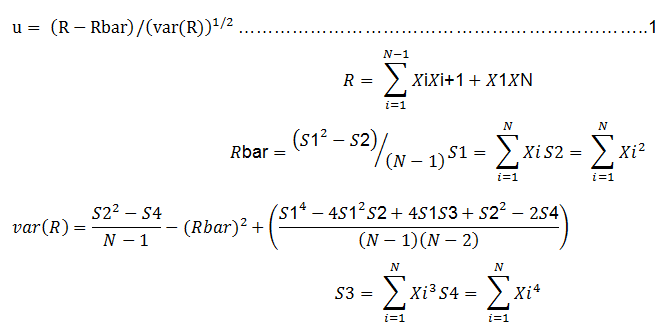
Where;
N = sample of size, Xi = daily maximum recorded rainfall data for each years.
Tests for homogeneity and stationarity
The homogeneity of maximum daily rainfall data recorded for each year (1987-2017) within the station was analyzed using test by comparing the static data set value (u) with the standard normal variate uα/2 corresponding to probability of exceedence ∂/2(5% significant level).
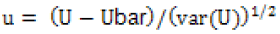 (2)
(2)
Ubar = p*q/2
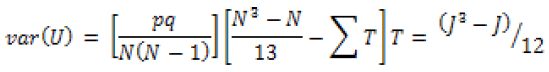
U = minimum value of V and W = MIN (V, W)
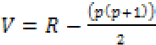 , W = pq-V
, W = pq-V
N = the combined data set of size (data from 1987-2017), N = p + q is ranked in increasing order; P = the first split sample size in the combined series (size N); q = the second split sample size in the combined series (size N), in this two sample of sizes p and q with p<=q are compared. R is the sum of the ranks of the elements of the first sample (size p) in the combined series (size N); J is the number of observations tied at a given rank.
Test for Outliers
The maximum daily rainfall data recorded from 1987 -2017 was checked for outlier’s data which might occur due to errors in data collection, or recording, or due to natural causes. Grubbs and Beck, 1972 as cited in Ramachandra, 2009) test was used to detect the low and high data outliers.
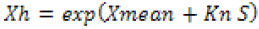 (3)
(3)
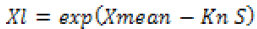 (4)
(4)
Where, X mean and S are the mean and standard deviation of the natural logarithms of the recorded maximum daily rainfall data, respectively, and Kn is the G-B statistic tabulated for various sample sizes and significance levels by Grubbs and Beck. It was estimated at 10% significance level using equation 5 as proposed by Pilon et al. 1985,Ramachandra, 2009) is used, where N is the sample size(from the year 1987-2017).
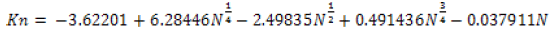 (5)
(5)
Sample values greater than Xh were considered to be high outliers, while those less than Xl were considered to be low outliers.
Probability of exceedence and Return period
Probability of exceedence and return periods for observed daily maximum rainfall was determined using equation 6 and 7 with Kimball’s method. The equation was given below;
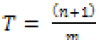 (6)
(6)
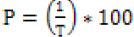 (7)
(7)
Where; T is returning periods (recurrence interval);
n is total number of data recorded years
m is the order number or rank of rainfall data(arranged in descending order of their magnitude in depth)
P is Probability of exceedence (the frequency) expressed as percent of that rainfall magnitude
Estimation of Design rainfall
Thirty one year’s observed daily maximum rainfall data were used for estimation of design rainfall intensity. Design rainfall of Beles Sugarcane command area was estimated using Gumbels normal frequency distribution method below.
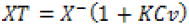 (8)
(8)
Where; XT = the probable of rainfall in mm, with return period of T years
Cv = coefficient of variation for thirty one year’s daily maximum rainfall data = ∂/ X-
∂ = standard deviation for thirty one year’s daily maximum rainfall data
X- = average for thirty one year’s daily maximum rainfall data
KT = frequency factor,
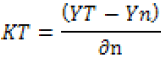
YT= reduced variant with return period,
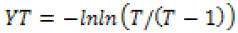
Yn, ∂n = expected mean and standard deviations of reduced extremes respectively which found from Gumbels table (Mashidani, 1978) for thirty one year’s.The design rainfall intensity of Beles Sugar Cane area for the designing of infield drainage networkswas suggested based on the existing condition of the command area.
The relation between observed rainfall data and the computed one using gumbel method were developedand quantified their deviation with the aid of regression trend line equation.
Data quality analysis
Independence and stationarity
According to equation 1 the independence of maximum daily rainfall data observed for year from (1987-2017) within the station was analyzed. The test value u=0.92 for the recorded data was less than the critical value at 5% signifance level u0.025=1.96. Thus, the maximum daily rainfall data observedat each year was independent. The statistical result was shown in Table 1.
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| N | S1 | S2 | R | S3 | S4 | R(bar) | var('R) | u |
| 31 | 2520.15 | 219028.2 | 206595.2 | 20423915 | 2046885231 | 204404.3 | 5663908 | 0.921 |
Homogeneity and stationary
According to equation 2 the homogeneity of maximum daily rainfall data observed for year from (1987-2017) within the station was analyzed. The test value u=1.67 for the observed data was less than the critical value U0.025=1.96 at 5% signifance level. Thus, the data observed among each year was homogenous. It means that there washomogeneity of maximum daily rainfall data among the observed year (there was a probability of similar distribution among years within the same station). The statistical result was shown in Table 2.
| Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p | q | N | R | V | w | ∑T | var(U) |  |
U | u |
| 14 | 17 | 31 | 266 | 161 | 77 | 0 | 634.67 | 119 | 77 | 1.67 |
Outlier’s data test
According to equation 3 and 4 the maximum daily rainfall data observed from 1987 -2017 was analyzed for high and low outliers respectively. Outlier’s data might be occurred due to errors in data collection, or recording, or due to natural causes. For the recording years, the high and low outliers analyzed were 151.3 and 41.0 mm. Among the recorded data there was no value greater than the high outliers (Xh =151.3 mm) and there was no value less than the low outliers (XL=41.0 mm). Therefore, there were no outlier’s data among the recorded years. The statistical result value and the distribution of maximum daily rainfall data were shown in Table 3 and Figure 2 respectively.
| Parameters | |||||
|---|---|---|---|---|---|
| N | Xmean | S | kn | Xh | Xl |
| 31 | 4.3662 | 0.2534 | 2.5778 | 151.32 | 40.975 |
Probability of Exceedance and Return Period
The probability of exceedence and return periods for the observed daily maximum rainfall data was determined using equation 6 and 7 respectively. According to table 4 the lowest daily maximum rainfall (48.6 mm) was recorded in 2011. It has a probability of 96.9% re-occurrence ones in every one (1) year. This means that 48.6 mm of maximum daily rainfall is likely to occur every one year. As shown in Table 4 the highest daily maximum rainfall (150.1 mm) was recorded in 1997. It has a probability of 3 .1%re-occurrence ones in every thirty two (32) years. This meant that 150.1mm of maximum daily rainfall is likely to occur three times in every 100 years period. The 54.8 % of the rainfall data was lessthan the average (81.3 mm). The probability of exceedence and return periods of the data was shown in the form of Figure 3 and Table 4 below;
| S.N | Year | Daily observed max rainfall, mm | Daily max rainfall in descending order | Rank, m | Return period, T(n+1/m) | Exceedence probability, P(1/T) in % |
|---|---|---|---|---|---|---|
| 1 | 1987 | 79.8 | 150.1 | 1 | 32.0 | 3.1 |
| 2 | 1988 | 105.8 | 115.8 | 2 | 16.0 | 6.3 |
| 3 | 1989 | 115.8 | 111.0 | 3 | 10.7 | 9.4 |
| 4 | 1990 | 65.2 | 108.2 | 4 | 8.0 | 12.5 |
| 5 | 1991 | 76.0 | 105.8 | 5 | 6.4 | 15.6 |
| 6 | 1992 | 86.7 | 99.0 | 6 | 5.3 | 18.8 |
| 7 | 1993 | 58.9 | 94.4 | 7 | 4.6 | 21.9 |
| 8 | 1994 | 94.4 | 90.8 | 8 | 4.0 | 25.0 |
| 9 | 1995 | 108.2 | 88.7 | 9 | 3.6 | 28.1 |
| 10 | 1996 | 90.8 | 88.4 | 10 | 3.2 | 31.3 |
| 11 | 1997 | 150.1 | 87.7 | 11 | 2.9 | 34.4 |
| 12 | 1998 | 87.7 | 86.7 | 12 | 2.7 | 37.5 |
| 13 | 1999 | 57.4 | 85.0 | 13 | 2.5 | 40.6 |
| 14 | 2000 | 72.4 | 84.8 | 14 | 2.3 | 43.8 |
| 15 | 2001 | 99.0 | 81.2 | 15 | 2.1 | 46.9 |
| 16 | 2002 | 62.6 | 79.8 | 16 | 2.0 | 50.0 |
| 17 | 2003 | 88.7 | 77.3 | 17 | 1.9 | 53.1 |
| 18 | 2004 | 71.8 | 74.7 | 18 | 1.8 | 56.3 |
| 19 | 2005 | 54.3 | 72.4 | 19 | 1.7 | 59.4 |
| 20 | 2006 | 66.2 | 71.8 | 20 | 1.6 | 62.5 |
| 21 | 2007 | 59.5 | 69.0 | 21 | 1.5 | 65.6 |
| 22 | 2008 | 81.2 | 66.2 | 22 | 1.5 | 68.8 |
| 23 | 2009 | 88.4 | 65.2 | 23 | 1.4 | 71.9 |
| 24 | 2010 | 85.0 | 64.7 | 24 | 1.3 | 75.0 |
| 25 | 2011 | 48.6 | 62.6 | 25 | 1.3 | 78.1 |
| 26 | 2012 | 69.0 | 61.5 | 26 | 1.2 | 81.3 |
| 27 | 2013 | 111.0 | 59.5 | 27 | 1.2 | 84.4 |
| 28 | 2014 | 61.5 | 58.9 | 28 | 1.1 | 87.5 |
| 29 | 2015 | 64.7 | 57.4 | 29 | 1.1 | 90.6 |
| 30 | 2016 | 74.7 | 54.3 | 30 | 1.1 | 93.8 |
| 31 | 2017 | 84.8 | 48.6 | 31 | 1.0 | 96.9 |
As shown in the figure 3, the relation between return period and observed daily maximum rainfall was mostly best fitted with logarithmic trends function (R2=0.963). y is daily maximum rainfall in mm whereas x is return period in year. It was fitted for Gumbel’s normal distribution method (since R2=0.963 and the data showed similar distribution as homogeneity test undertaken above).
Estimation of Design rainfall
Design rainfall for different return periods was determined using equation 7, Gumbels normal frequency distribution method. As the computed rainfall result showed in the Table 5, there was a similar distribution with the observed rainfall data. Within the same ten years return period, the computed rainfall (114.7 mm) was deviate by 0.04 with the observed rainfall (110.3 mm). The observed design rainfall value for ten years return period was obtained by interpolation using Table 4 (column four and six). The observed design rainfall value for the other different return periods within thirty two years which was not stated in the table 4, it can be obtained using interpolation of column four and six. As shown in Table 4, the observed data was available for thirty one years and its return period was only up to thirty two (32) years. But, most of the large hydrological, irrigation and drainage structures commonly need at least 50 years return period. In order to consider long return periods which haven’t available rainfall data, use of frequency distribution method is very important. Thus, in this study maximum daily design rainfall up to 200 return periods were computed as per Gumbels normal frequency distribution method (Table 5). The design rainfall that was computed using gumbel method was shown in Figure 4 and Table 5 below;
| Return period ,T | ||||||||||||
| Computed Rainfall, mm | 5 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 |
| 100.0 | 114.7 | 128.7 | 136.7 | 142.4 | 146.8 | 150.4 | 153.4 | 156.0 | 158.3 | 160.4 | 173.9 | |
According to, five metrological stations; Bhirdar, Dangila, Enjibara, Pawi and Gonde were combined used to develop regional based intensity duration frequency curve. The location, elevation and rainfall of these stations are mostly quite differ from the Beles Project command area except Pawi station which is close to the command boundary area as stated and shown in the description area map (Figure 1). As regional intensity duration frequency curve, the rainfall intensity of ten years return period for duration of 0.5hr, 1hr, 2hr, 3hr, 6hr ,12hr and 24hr were 20.6, 28.8, 34.5, 37.6,42.7,47.8 and 53.0 mm depth respectively. The gap of this study was that, it wasn’t site specific, not updated (most of the data used were up to 2006 years) and some of stations had limited data size, but in this study thirty one year’s pawi station data up to 2017 years were used, the station used was close and representative to the command area. According to this study was used gumbel distribution method to determine design rainfall intensity for ten years return period which was an input for estimation of surface runoff. Due to the limited data availability as stated in the report, twenty four (24) hour of nineteen years (19) rainfall of pawi station was used. The limitation of this study was the data size availability; there was ambiguity in determination of design rainfall (242mm depth and 61mm/hr for1hr duration) which wasn’t clear, the data used was up to 2006 and also design rainfall considered was only for ten years return period which was specific and it didn’t provide others different return period to see alternate options. But, in this study different return periods up to 200 years were considered with respect to design rainfall depth (Table 5). Within the above similar gumbel distribution method and ten years return periods, 114.7 mm depth of design rainfall was obtained in this study. Therefore, the hydrologist, Hydraulic and Irrigation Engineers has to better consider these design rainfalls with respect to its return periods that was obtained in this study for hydrological, irrigation and drainage design works which have been executed in the Beles Sugar Project.
Comparison of Observed and Computed rainfall using regression function
The relation between the observed and computed rainfall data using regression (trend line) function was undertaken and shown in Figure 5. The average deviation of the observed rainfall data from its trend line function (with R2=0.96) was 0.004 above or below. The average deviation of the computed rainfall data using trend line function (with R2=0.97) was 0.002 from the observed data. For large return periods which hadn’t available rainfall data (at least more than 30 years), the deviation of rainfall using the gumbel computed trend function was nearest to the observed rainfall data rather than the value that was obtained using observed trend function. Thus, the gumbel computed trend line function gave result values nearest to the observed daily maximum rainfall data.
As show in Figure 5, the design rainfall data for large return periods which hadn’t available rainfall data which were estimated using the gumbel computed trend line function (y = 25.484ln(x) +57.173) were given in Table 6 below. Where, y is design daily maximum rainfall in mm, x is returning periods in years. The correlation between observed rainfall data and rainfall data obtained using computed trend line function within the same return period was 0.98, thus it is highly correlated and reality was perfect.
| Design daily maximum Rainfall, mm | Return period, years | |||||||
| 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | |
| 151.2 | 156.9 | 161.5 | 165.4 | 168.8 | 171.8 | 174.5 | 192.2 | |
Estimation of peak flood flow rate for a desired return period is a pre-requisite for planning, design and management of hydrological, hydraulic, drainage structures, barrages, dams, spillways, bridges, culverts and so on. Beles Sugar Development Project is expected to cover 50,000 ha of net irrigated command area with sugarcane crop. In view of this, there will be design, construction and operational activities for the purpose of hydrological, irrigation and drainage structural works. Design rainfall intensity is significant to estimate peak runoff for the design of these stated structures. Thus, this study was conducted to study design rainfall of Beles Sugar Development project command areas for different desired return periods.
The data quality was checked using different tests. Thus, the data was independent and homogenous among the recorded period. The recorded data was checked for outlier, among the recorded data there was no value greater than the high outliers 151.3 mm and there was no value less than the low outliers 41.0 mm. Therefore, there were no outlier’s data among the recorded years. The probability of exceedence and return periods for recorded daily maximum rainfall were stated in Table 4.
Design rainfall for different desired return periods was determinedand shown in table 5 accordingly. The computed design rainfall was deviate by 0.04 with the observed rainfall. The average deviation of the observed rainfall and computed rainfall data from their trend line functions were 0.004and 0.002 above or below. The correlation between the observed rainfall and computed data of trend line function was 0.98, thus it is highly correlated and the reality was perfect. The gumbel computed trend line function gave result values nearest to the observed daily maximum.
The limitation of previous studied works that were elaborated and referred in the result and discussion part 3. Thus, this study used at least thirty one year’s data up to 2017 which was more representative to project command areas. Therefore, the project irrigation engineers has to be better consider, aware and access this study for hydrological, irrigation and drainage design works which have been executed in the Beles Sugar Project. For design of small hydrological and drainage structures which need at least for 30 years return period was given in Table 4.
10 years return period is mostly used for estimation of design rainfall for open earth farm drainage channels. However, it is up to the engineer’s decision. In practical condition, the open earth drainage channels are deformed through a time being where its size mostly becomes enlarged due to erosion, structural damage such as re-correction or shaping works. The design rainfall size is increasing with respect to increasing return period. Therefore, 10 years return period for fixing the drainage channel size is adequate. Having this, design rainfall for 10 years return period was suggested for estimation of Beles Sugarcane open earth drainage channels. Accordingly, the design rainfall is 110.3 mm. By taking 110.3 mm as an average of three hours storm which is commonly occurred in the command area. Therefore, design rainfall intensity occurred per hour is 36.8 mm/hr.
Based on the study of design rainfall result for the case of Beles Sugar Development project irrigation command areas, the following recommendations were forwarded;
➢ For the small size design, construction, operation and modification of hydrological, hydraulic, drainage structures, culvert that have been executed in the project which needs at least 30 years return period and below was suggested as per Table 4. For the case of Beles Sugarcane open earth drainage channels 36.mm/hr was suggested.
➢ For the design, construction, operation and modification of hydrological, hydraulic, drainage structures, barrages, dams, spillways, bridges, culverts that have been executed in the project which needs at least (40, 50,60,70,80,90,100 and 200 years return period);151.2, 156.9, 161.5, 165.4, 168.8, 171.8, 174.5 and 192.2 mm of design rainfall were suggested respectively(as per Table 6).
➢ The Project Engineers and Hydrologists has to considered and access this data pre-requisite for planning, design and management of hydrological, hydraulic, drainage structures, barrages, dams, spillways, bridges, culverts and so on that have been executed in the Beles Sugar Development Project.
➢ There was a gap on daily rainfall intensity duration. Therefore, the organization should support and monitored for the availability and functioning of automatic rain recorder.
Irrigation & Drainage Systems Engineering received 835 citations as per Google Scholar report