Research - (2023) Volume 17, Issue 1
Received: 08-Jan-2023, Manuscript No. glta-23-86156;
Editor assigned: 09-Jan-2023, Pre QC No. P-86156;
Reviewed: 23-Jan-2023, QC No. Q-86156;
Revised: 28-Jan-2023, Manuscript No. R-86156;
Published:
03-Feb-2023
, DOI: 10.37421/1736-4337.2023.17.371
Citation: Yadav, Sarasvati and Shaifali Thakur. â??Study on Models of the Lie Algebra Gu,v via Euler Integral Transformation.â? J Generalized Lie Theory App 17 (2023): 371.
Copyright: © 2023 Yadav S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In this paper, we construct two variable and three variable models of the irreducible representation of Lie Algebra Gu,v. The two variable models are then transformed in terms of difference-differential operators using the Euler integral transformation while the three variable models are transformed in terms of difference-differential operators using the two-fold Euler integral transformation. These models are then used to obtain some generating functions and recurrence relations.
Simplicial operad • Brace algebra • Hochschild cohomology
The connection between the Lie theory and the special functions plays a crucial role in the formalism of Mathematical Physics, handing a consolidated formalism to deal with the aggregate of special functions and a collection of formulas such as the integral representations, differential equations, composition theorems, recurrence formulae, etc., Within the group-theoretic context, a given class of special functions appears as a set of matrix elements of irreducible representations of a given Lie group. The algebraic properties of the group are then reflected in the differential equations satisfied by a given family of special functions, while the geometry of the homogeneous space ascertain the nature of the integral representation linked with the family. Authors like Miller W [1] deal with 3-, 4- and 5- dimensional Lie algebras where the special functions appeared as matrix elements of the corresponding group operators and also as basis functions of the representation spaces [2-4]. The connection between the Lie algebras and Lie groups has been discussed and the realization of the representation has been connected with special functions, Monocha HL discussed the two and three variable models of sl(2, C) and G(0, 1), i.e. the 3-and 4-dimensional Lie algebras and then use Mellin transformation to obtain new models in terms of difference- differential operators [5,6]. Sahai V and Yadav S discussed the relation between p, q-analogue of special functions and representations of certain quantum algebras of two parameters [7-9]. The Author computed the matrix elements of their representations in terms of the generalized p, q-hypergeometric series, Sahai V and Srivastava Y constructed three variable models of Lie algebra T3 and then use Euler integral transform to transform the models in terms of the difference-differential operator, Chakrabarti R and Jagannathan R studied quantum algebra sup,q(2) and its two parametric deformation [10,11].
In the present study, we construct two variable and three variable models of the representation of Gu,v in terms of differential operators. Then we make use of Euler integral transformation to transform the two variable models in terms of difference-differential operators acting on basis functions acting on the Gaussian hypergeometric functions and we use two fold Euler integral transformation to transform the three variable models in terms of difference differential operators acting on basis functions acting on the product of two Gaussian hypergeometric functions.
Section-wise coverage is as follows:
• In section 2, we review various definitions and theorems needed for our discussion.
• In section 3, we construct new two variable and three variable models of Lie Algebra Gu,v acting on basis function involving 1F0 and the product of 1F0 functions respectively.
• In section 4, we have used one-fold and two-fold Euler Integral transformation to derive some results to be used in our further work.
• In section 5, we reform two variable and three variable differential models of Gu,v acting on basis functions involving 2F1 and product of 2F1 functions with unit argument respectively.
• In section 6, we compute several new generating functions and recurrence relations obtained from this study.
Lie Algebra Gu,v
The Lie Algebra Gu,v=L{Gu,v} as defined in is the three dimensional complex Lie algebra with basis J+, J−, J3 and commutation relations [12]:
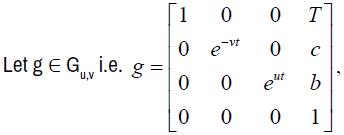
where b, c, τ ∈ C; u, v are relatively prime positive integers, u is odd.
Elements of the Lie algebra Gu,v are of the type
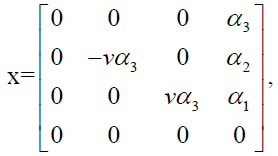
where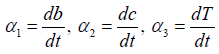 
are in the neighbourhood of identity.
Basis elements for the Lie algebra Gu,v are
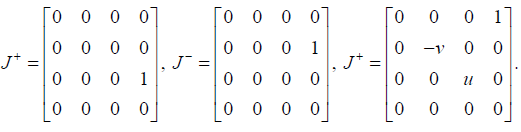
Let ρ be an irreducible representation of the Lie algebra Gu,v on the vector space V and let J±=ρ(J±), J3=ρ(J3), then the operators J±, J3 satisfy the same commutation relations as (1).
Define the spectrum S of J3 to be the set of all eigenvalues of J3.
Further, let the irreducible representation ρ satisfies the condition:
Each eigenvalue of J3 has multiplicity equal to one. Then there is a countable basis for V consisting of all the eigenvalues of J3. This guarantees that S is countable and that there exists a basis for V consisting of vectors fm such that J3fm=mfm.
From [13], a one variable model of the irreducible representaion is given by:
Representation Qu,v(ω, m0)
where m∈ S={m0+n: n is an integer}.
For each representation Qu,v(ω, m0), there is a basis for V consisting of vectors fm, defined for each m∈ S, such that
Generating functions
Consider a two variable function F (z, t) which possesses a formal (not necessarily convergent for t≠0) power series expansion in t given by
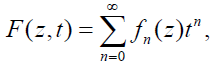
where fn(z) is a function of z in general for n=0, 1, . . . . Then the expansion (??) is said to have generated the set fn(z) and the function F(z, t) is called the linear generating function or generating function for the set fn(z). The above relation (??) is called the generating relation for the set fn(z).
Recurrence relation
A recurrence relation for a function f(n) is an equation that expresses f(n) in terms of one or more of the previous values of the function f(n).
For example: Recurrence relation for Legendre’s polynomial P(n) is:
(n+1)Pn+1(x)=(2n+1)xPn(x) − nPn−1(x).
In this section, we presented the two variable and the three variable models of the Lie algebra Gu,v. Also, we examined multiplier representation of the local Lie group Gu,v induced by the operators on F, the space of all analytic functions in the neighbourhood of (x0, y0) and (x0, y0, t0) respectively.
Two types of two variable models are constructed and following are their representations:
Type 1
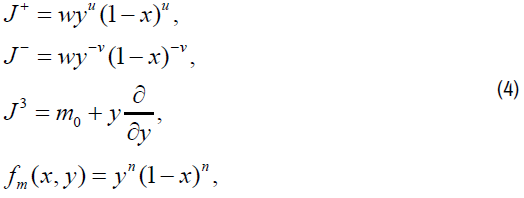
where m∈ S={m0+n: n is an integer}.
The multiplier representation A1(g)f of the Lie group Gu,v induced by the operators on F is
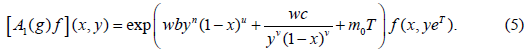
Type 2
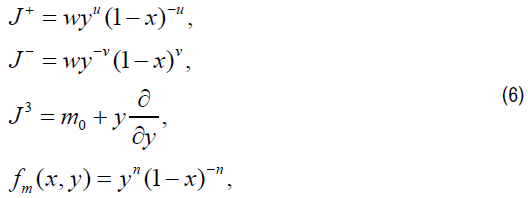
where m∈ S={m0+n: n is an integer}.
The multiplier representation A2(g)f of the Lie group Gu,v induced by the operators on F is
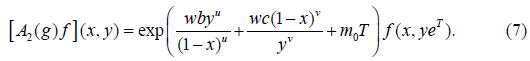
Four types of three variable models are constructed and following are their representations:
Type 3
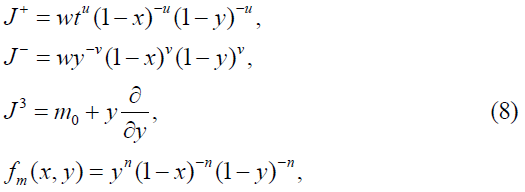
where m∈ S={m0+n: n is an integer}.
The multiplier representation T1(g)f of the Lie group Gu,v induced by the operators on F is
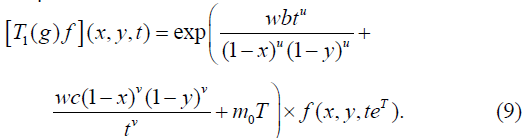
Type 4
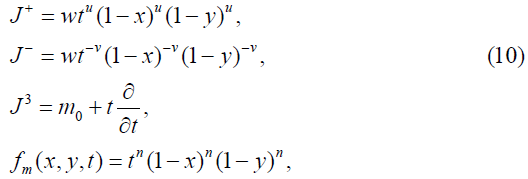
where m∈ S={m0+n: n is an integer}.
The multiplier representation T2(g)f of the Lie group Gu,v induced by the operators on F is
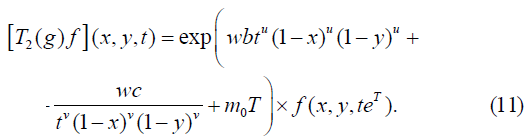
Type 5
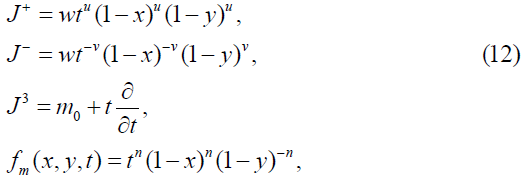
where m∈ S={m0+n: n is an integer}.
The multiplier representation T3(g)f of the Lie group Gu,v induced by the operators on F is
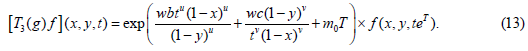
Type 6
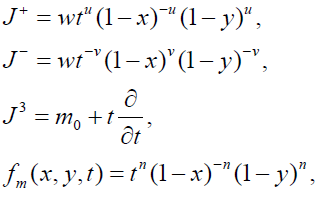(14)
where m∈ S={m0+n: n is an integer}.
The multiplier representation T4(g)f of the Lie group Gu,v induced by the operators on F is
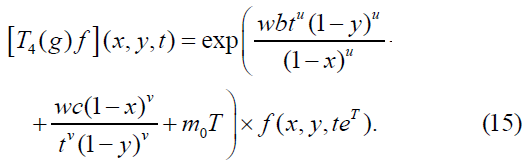
Euler Integral Transformation
One fold Eeuler transformation
Let V be the complex vector space of all functions f(x), expressible as a power series about x=0. We use [14],
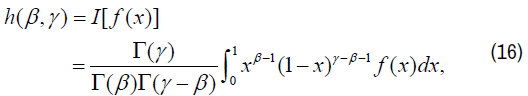
Re γ ≥ Re β ≥ 0.
Then, W=IV is an isomorphic image of V under the transformation I: f(x) → h(β, γ). Now we obtain transform of certain expressions, needed for our discussion, under the transformation I in terms of difference operators defined as:
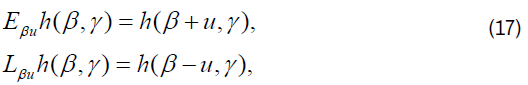
The following are the transformations under I:
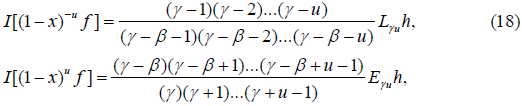
Two Fold Euler transformation
Let V be the complex vector space of all functions f(x), expressible as a power series about (x, y)=(0,0). We use [15],
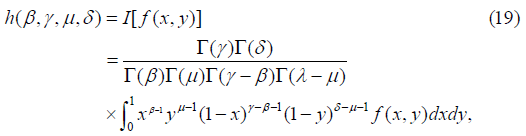
Re γ ≥ Re β ≥ 0, Re δ ≥ Re μ ≥ 0.
Then, W=IV is an isomorphic image of V under the transformation I: f(x,y) → h(β, γ, μ, δ). Now we obtain transform of certain expressions, needed for our discussion, under the transformation I in terms of difference operators defined as:
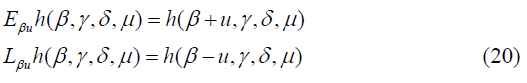
The following are the transformations under I:
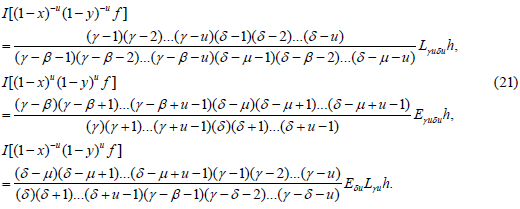
In this section, we transformed the aforementioned two variable and three variable models in terms of difference-differential operators with the basis functions appearing in terms of hypergeometric functions. For this, we use a theorem as in [6].
Theorem: Let ρ be an irreducible representation of Gu,v in terms of basis operators {J3, J+, J−} on a representation space V with basis functions {fm: m ∈ S}. Then the transformation I induces another irreducible representation σ of the Lie algebra Gu,v on the representation space W=IV having basis {hm: m ∈ S} in terms of operators {K3,K+,K−}, where
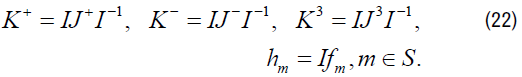
That is, ρ and σ are isomorphic.
We present below the transforms of models of Type I, II, III, IV, V and VI introduced in section 3.
Type I’
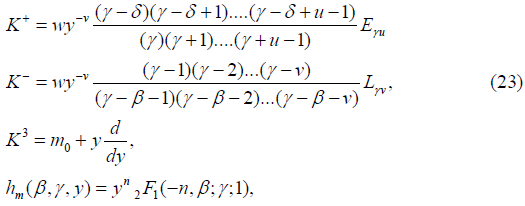
where m ∈ S={m0+n: n is an integer}.
Type II’
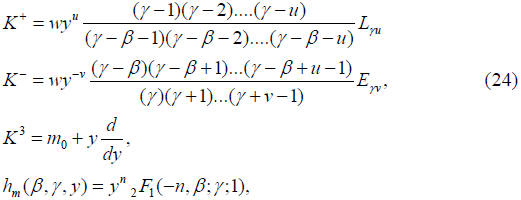
where m ∈ S={m0+n: n is an integer}.
Type III’
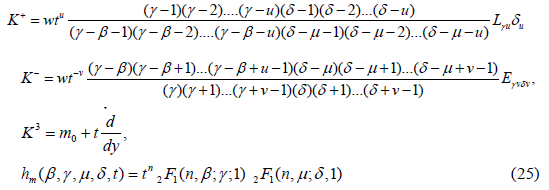
where m ∈ S={m0+n: n is an integer}.
Type IV’
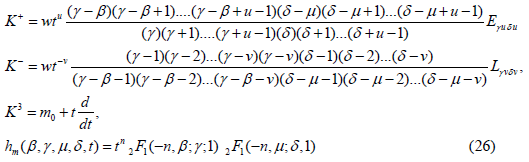
where m ∈ S={m0+n: n is an integer}.
Type V’
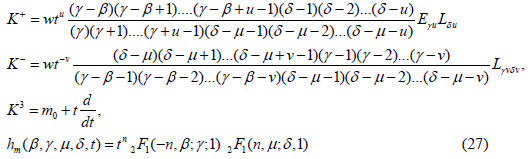
where m ∈ S={m0+n: n is an integer}.
Type VI’
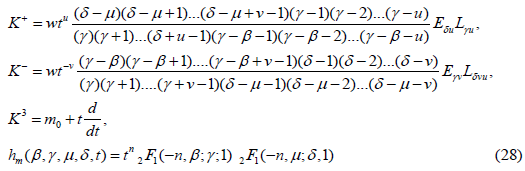
where m ∈ S={m0+n: n is an integer}.
The above models satisfy the following:
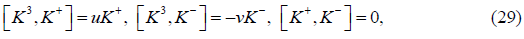
and thus lead to representation of Gp,q Also,
In this section, we have used models of Type I, II, III, IV, V and VI for obtaining generating functions and the transformed models of Type I’, II’, III’, IV’, V’ and VI’ for obtaining recurrence relations. We present the results as follows:
Generating functions
Introducing new group parameters r, h defined by b=rhu/(u+v) and c=rh−v/(u+v) and then putting τ=0, h=1, ω=1, k=0 in equation (5), (7), (9), (11), (13) and (15), we get
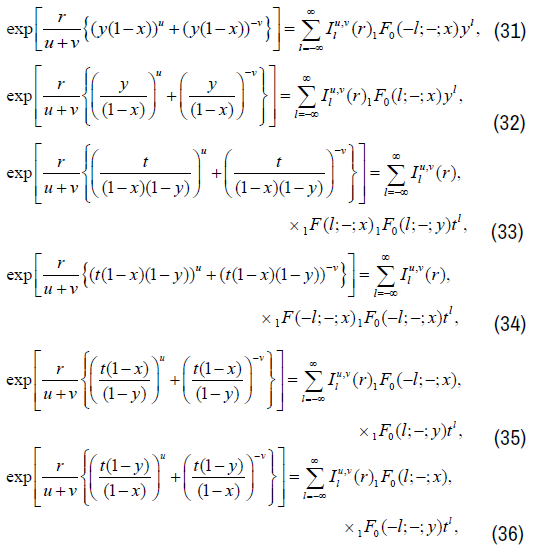
where,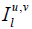 
is the group theoretic generalization of Bessel functions and is defined as in [1],
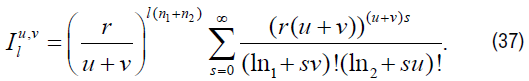
Recurrence relations
From Model of Type I’, we get
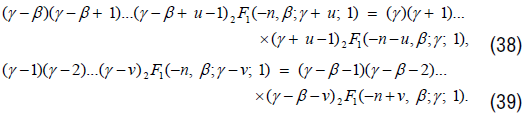
Similarly, we get recurrence relation from Models of Types II’, III’, IV’, V’ and VI’ and are as follows:
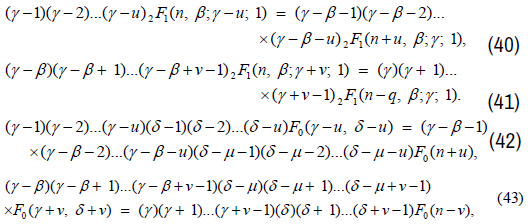
where in (42) and (43), F0 stands for
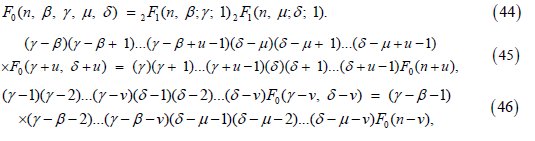
where in (46) and (47), F0 stands for
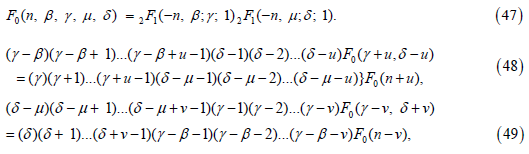
where in (49) and (50), F0 stands for
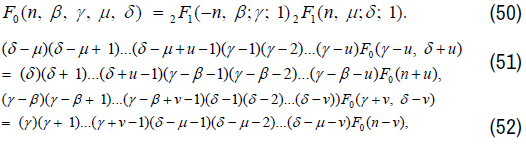
where in (52) and(53), F0 stands for
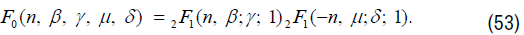
It is widely known that the special function theory has a vast body of literature, The findings of this study not only add to the body of knowledge but also shed light on how group theory and special function theory relate to one another. It is asserted that these identities and recurrence relations are novel. However, the literature does contain specific cases of these generating functions. For instance, when u, v=1, we have the same outcomes as in.
The financial assistance provided to the second author in the form of UGC (JRF) fellowship (1094/CSIR-UGC NET JUNE 2019) from UGC, New Delhi, India is gratefully acknowledged.
None.
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
Google Scholar, Crossref, Indexed at
