Temperature Distribution along the Production Well Bore

Gunel Imanova^1*, Rzayev Ab. G¹, Asadova Rena Sh¹ and Gurbanov Z.G^2
*Correspondence: Gunel Imanova, Department of Physical, Mathematical and Technical Sciences, Institute of Control Systems of the Azerbaijan National Academy of Sciences (ANAS), Baku, Azerbaijan, Email:

Keywords

Heat exchange • Heat transfer • Temperature distribution • Geometric gradient • Thermal conductivity • Mathematical model

Introduction

Numerous works are devoted to the issues of operating temperature of oil production wells (OPW), in which various aspects of this complex phenomenon are discussed [1-3]. As a result of analytical research on this issue, a significant number of solutions to the thermal conductivity equation describing temperature processes occurring during the movement of formation fluid along the OPW borehole were obtained.

Formation of asphaltene-resin-paraffin deposits (ARPD) on the surface of downhole equipment and production casing (PC) is one of the main complications in OPW operation, which decreases the cross-sectional area of OPW casing and increases formation fluid flow viscosity and flow resistance. On the other hand, the thickness of the boundary layer increases, resulting in reduced heat loss. For successful ARPD prevention and removal measures, it is necessary to know the depth of the beginning of paraffinization of the wells [4-6].

Analysis of field data has shown that intensive ARPD formation occurs at fluid temperatures below the temperature of oil saturation with paraffin (paraffin crystallization) [2]. The process of paraffin adhesion takes place on the inner surfaces of the tubing and PC, which significantly decreases the coefficients of thermal conductivity (λ) and heat transfer (K) from the fluid flow to the environment, i.e., to the rock. Therefore, it is necessary to determine the temperature distribution in the tubing and PC with sufficient accuracy for practical purposes in order to detect ARPD formation points and develop technological measures for their removal or prevention of their formation.

Methodology

Problem statement

In theoretical research of heat conduction through the cylindrical walls of the tubing and PC it is assumed that the rocks in the well section are homogeneous and isotropic; the rocks are horizontal and heat conducting flows in the well are close to the radial (if the fluid moves in the well at a constant flow rate and with certain friction pressure losses); there are no phase transitions (ARPD formation) or other processes associated with release or loss of energy, etc. However, in practical operation of oil reservoirs, OPW operation is accompanied by phase transitions related to the saturation of oil with ARPD components, deposition (adhesion) of these components on the inner surfaces of the tubing and PC and uneven distribution of the composition and flow rate in the latter. In addition, along with heat conduction the process of heat exchange is also carried out by convective heat transfer; temperature variation along the OPW borehole is a synergism (joint action) of thermal processes occurring both in the oil reservoir and in PC and the tubing boreholes; at the same time, temperature distribution in vertical (upward) fluid flow from the bottomhole (perforation point) of the well to the suction valve of the tubing pump significantly differs from temperature distribution along the tubing height (from the suction valve of the tubing pump to its wellhead); in the first case heat transfer is intensive, because as heat transfer is between the upward fluid flow and the rock and the flow rate is much lower than in the tubing; and in the second case the heat transfer is between the upward fluid flow and the fluid and gas layer in PC. Consequently, development of mathematical models to estimate the temperature distribution along the height of OPW (along the PC and the tubing), taking into account the above factors and geometric gradient of the rock is a relevant problem and is the subject of this article.

Solution

In the course of the study, it was found that the temperature distribution (TD) along the OPW height from the bottomhole (perforation point) to the wellhead is a complex process and depends on many factors, such as well depth and pump running, pump immersion under dynamic level, formation temperature and decline, gas factor and chemical composition of formation fluid (water-oil mixture), chemical composition and geometric gradient of the rock, water cut and rheological characteristics of oil, ARPD on the PC and the tubing walls, etc. TD also depends on the intensity of heat conduction through the tubing and PC walls and convective heat transfer by upward fluid flow. Consequently, taking these factors into account makes it possible to get a more adequate mathematical model of TD along the height of the tubing and PC of OPW.

In view of the above, this article proposes two variants of new mathematical models of estimating TD along the height of PC and the tubing of OPW.

Results and Discussion

First, we will consider the process of developing a mathematical model to estimate TD along the length (height) of the PC from the bottomhole, taking into account the geometric gradient (Gt) of the rock, heat conduction and convective heat flows.

Fluid temperature distribution along the length (depth) of the PC of OPW. Heat conducting flows (HF) in homogeneous horizontal rocks in the nearwellbore zone will be very close to radial. The flow rate of HF in the height element dZ1 (hereinafter index 1 will denote PC and index 2 will denote the tubing of OPW) at a constant temperature difference ΔT1(Z1) between the rock and the fluid flow can be determined from the following exact formula

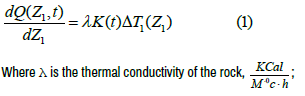
Ð?(t) is a dimensionless coefficient of heat exchange between the fluid flow and the environment, depending on the HF geometry and time. For radial flow around the wellbore, the coefficient K(t) is calculated with high accuracy [1] using the formula

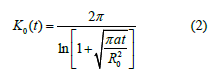
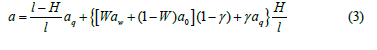
Where Re is the radius of PC, m; a is thermal diffusivity, m^2/s; H, l are the dynamic fluid levels in PC and OPW depth, m; W, γ are the water cut and gas factor of the produced oil, fraction; aq, aw, ao are thermal conductivity of gas, water and oil, m^2/s. In the case of a variable temperature difference, equation (1) takes the form of a convolution [1].

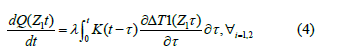
Using the basic energy equation described for a horizontal flow in a porous oil reservoir environment, in our case for vertical flow in the borehole of PC and the tubing with porosity m=1, equation (4) takes the following form:

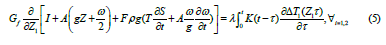
where G=Fρω is the mass flow rate of the upward fluid flow, kg/s; ρ, ω is the density, kg/m³ and the flow rate, m/s, of the fluid; F is the cross-sectional area of the fluid flow stream in PC and the tubing, m²; I, S are thermodynamic functions, specific enthalpy, kcal/kg and entropy, respectively, kcal/(kg.0C); А is the heat equivalent of work, kcal/kg.m; Z is the height mark, m.

Equation (5) is solved using the relation:

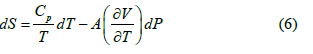
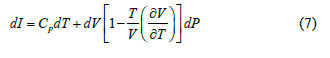
With a constant fluid (formation fluid) flow rate G_0 in the bore of the PC of constant cross section and the condition Z > ωt, ∂ω/∂Z=0; ∂P/∂t=0; ∂P/∂Z1=(Pw –Pm)/l; ω=G0/(Fρ). As a result, we get:

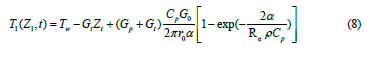
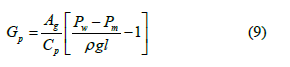
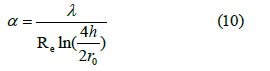
where Gt is the geometric gradient, 0C/m; GP is the temperature gradient by pressure, 0C/m; Pw, Pm are the pressure at the bottomhole and at the wellhead of PC of OPW, Pa; Cp is the heat capacity of the fluid at constant pressure, kcal/(kg.0C); h is the thickness of the rock, m.

Then obtained mathematical expressions (8)-(10) are temperature distributions (TD) along the length (depth) of the PC of OPW.

Fluid temperature distribution along the length of the tubing of OPW

TD along the length of the tubing is completely different from TD along the length of PC of OPW; this fact is significant when OPW has great depth (≥ 3 km), the dynamic fluid level in PC is low and the depth of pump immersion into the dynamic fluid mixture layer is insignificant (≤ 100 m); when fluid flows from the pump discharge valve to the wellhead of the lifting tubing, the change of its temperature due to heat transfer to the pipe string occurs through heat conduction in the laminar boundary layer (LBL) by convection in the turbulent core (TC). Moreover, depending on the characteristics of LBL and TC, the heat transfer also changes. Since heat transfer by convection is incommensurably more intense than heat conduction, the temperature variation in any flow cross section should be insignificant, which is confirmed by experimental data. A geometric interpretation of heat transfer in an oil production well is shown in Figure 1.

1 – tubing; 2 – PC; 3 – rock; 4 and 5 – walls of the tubing and PC, respectively; l – well depth, m; Н – dynamic fluid level in PC, m; x, z – horizontal and vertical coordinates, m; tf1, tf2, – fluid flow temperatures in the tubing and PC, °Ã¡; r_i,r_o – inner and outer radius of the tubing wall, m; R_i,R_o – inner and outer radius of the °C wall, m; δ – the thickness of the boundary layer consisting mainly of ARPD, m; λ_w – thermal conductivity of the wall material, kcal/(m.h. °C); tÃÂ?₁, tÃÂ?₂ – temperature of the outer surfaces of the tubing wall, °Ã¡; ∝₁,∝₂ – coefficients of heat transfer in the flows in the tubing and PC, respectively, kcal/(m².h. °C).

Below is a mathematical model of the heat transfer process in the tubing:

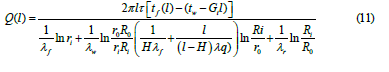
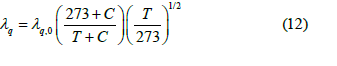
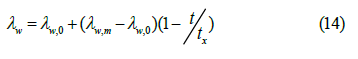
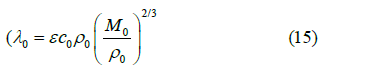
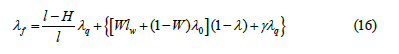
where λ_q, λ_w, λ_w, λ₀, λ_f are thermal conductivity of gas, tubing and PC walls, water, oil and fluid, respectively, kcal/(m.h. °Ã¡); tf,tw are fluid temperature and bottomhole temperature, °Ã¡; τ is time, h; λ_q,0, λ_w,0, λ_{w ÃÂ??,0} are values of λq, λ_w, λ_w ÃÂ?? in normal conditions (t=0°Ã¡); С is determined experimentally, °Ã¡; W,γ are water cut and gas factor of the produced fluid, fraction; b is the empirical coefficient, 1/°Ã¡; t is temperature, °Ã?; t_x is characteristic value of T, determined using the method of tangent to the exponential curve, °Ã?.

To determine the temperature variation along the length of the lifting tubing, we can use formulas (8), (10), replacing the geometric gradient Gt with the temperature gradient in the liquid and gas layer of PC Gt and the thermal conductivity of the rock λ with the thermal conductivity of the liquid and gas λ_fq

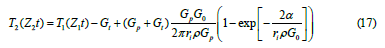
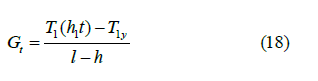
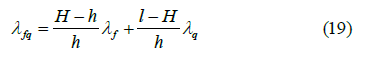
Where T₁ (h₁t) is the pump inlet temperature, °Ã¡; T_1y is the temperature at the wellhead of PC, °Ã¡.

The physical meaning of these solutions is interpreted in Figure 2 in coordinates [h, T].

The straight line А₀С₀ depicts a geotherm, i.e., the temperature distribution in the wellbore before its start-up time t ≤ 0. The Ð?₀С₀ curve corresponds to the steady temperature in the wellbore after the well is started in case of constant bottomhole temperature ΔТ(0, t)=0.

After the start of the well with constant withdrawal, the temperature in PC is represented by lines 1, 2, 3, etc., parallel to geotherm А₀С₀. Consequently, the temperature in the wellbore increases uniformly at all depths from the wellhead to the point of intersection of the stationary temperature curve at point Сπ, which moves upward at the flow rate ω. For instance, for the time instant t₂, the temperature profile in the wellbore is represented by the curve С₀ С₂ А₂. The condition of maximum temperature rise in the flow over the geometric curve follows from (8) for t→∞

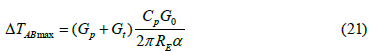
As noted above, the temperature variation along the length of the lifting tubing is insignificant compared to the temperature variation along the length of PC, since the environment (mainly the gas column in the annular space (between the tubing and PC) is much less thermally conductive than the rock. Hence, as it is seen from Figure 2, the line D4B0 characterizing the temperature variation along the length of the lifting tubing is not parallel to the line of geothermal gradient, but has minimal slope from perpendicular line. This is due to the fact that the fluid in the annular space (between the tubing and PC) has much lower thermal conductivity than the rock (Table 1).

Thus, obtained expressions (1)-(20) are mathematical models of the temperature variation along the length of PC and the lifting tubing of OPW.

Conclusion

An analysis of the state of the art of the problem of heat transfer in the production casing (PC) and the lifting tubing of an oil production well (OPW) is carried out. The schematic diagram of heat transfer by convection and heat conduction processes in OPW is proposed. Mathematical models for determining the temperature variation along the height of PC and the tubing are developed, allowing to adequately assessing the temperature distribution in the latter. It is shown that the temperature variation along the length of the lifting tubing significantly differs from the temperature distribution in PC, while the deviation of the temperature curve for the lifting tubing from the perpendicular is insignificant.

Conflict of Interest

No potential conflict of interest was reported by the authors.

References

1. Chekalyuk, E. B. "Thermodynamics of oil reservoir." Nedra, Moscow (1965).
2. Wiktorski, Ekaterina, Catherine Cobbah, Dan Sui and Mahmoud Khalifeh, et al. "Experimental study of temperature effects on wellbore material properties to enhance temperature profile modeling for production wells." J Pet Sci Eng 176 (2019): 689-701.

Google Scholar, Crossref, Indexed at

3. Areshev, Ye G., Plynin V.V., Popov O.K. and Shtyrlin V.F, et al. “Nature of anomalous data of thermohydrodynamic survey of oil wells // Moscow.” Neftyanoye khozyaystvo (2000): 41-47.
4. Rzayev, Abbas, Gambar Guluyev, Agayev Bikes and Abdurrachmanova Asude, et al. "Determining oil well debit Using oulet temperature information processing." Int J Manag Sci Eng Manag (2013): 55-64.

Google Scholar, Crossref, Indexed at

5. Rzayev, Abbas, Gambar Guluyev, F.H. Pashayev and As H. Rzayev, et al. "Mathematical models for determining the distribution of fluid flow temperature along the wellbore and horizontal pipeline." Int J Mechatron 21 (2020): 337-347.

Google Scholar, Crossref, Indexed at

6. Mishchenko I.T. “Downhole oil production.” Neft I Gaz (2003): 316.