Review - (2024) Volume 14, Issue 1
Received: 19-Jan-2024, Manuscript No. JBL-24-125414;
Editor assigned: 23-Jan-2024, Pre QC No. JBL-24-125414;
Reviewed: 05-Feb-2024, QC No. JBL-24-125414;
Revised: 12-Feb-2024, Manuscript No. JBL-24-125414;
Published:
20-Feb-2024
, DOI: 10.37421/2165-7831.2024.14.317
Citation: Srivastava, Rashmi and Swati Mishra" Temperature
Distribution of Blood Flow Through W-Shaped Tapered Stenosis Artery." J
Blood Lymph 14(2024):317.
Copyright: © 2024 Srivastava R, et al. This is an open-access article distributed under the terms of the creative commons attribution license which permits unrestricted
use, distribution and reproduction in any medium, provided the original author and source are credited.
The blood flow through w-shaped tapered artery in the presence of catheter is discussed. The equations governing the fluid flow have been solved analytically under the assumption of the mild stenosis. The blood flow behavior through the w-shaped stenosed artery is considered using the Prandlt fluid model and the flow of blood is considered as suspension of nano-particles. The analysis with respect to various parameters arising out of fluid and geometry considered, on temperature distribution of the w-shaped stenosis as well as across the entire length of the stenosis has been reported. Heat transfer phenomena have been examined for the physical features of the flow of blood through a stenosed artery, which is tapered in shape and with the presence of a clot. The temperature profile has been discussed with graphs for several different parameters of clot size, stenosis height, heat source, and sink parameter. It is observed that in converging tapering the temperature provides greater values as estimated together with the non-tapered arteries and diverging tapering arteries
Cardiovascular systems • Dimensionless • Governing equation• Stenosis arteries • Parameters • Tissues
Stenosis, a medical term which means narrowing of an artery, tube or orifice, is the abnormal and unnatural growth in arterial wall thickness that develops at various locations of the cardiovascular systems under diseased conditions. The actual causes of stenosis are not well known but it has been suggested that the deposits of cholesterol on the arterial wall and proliferation of connective tissues may be reasonable for the same (Chaturani and Ponalagusamy, Young, Shukla et al.) [1-3]. Stenoses lead to circulatory disorders such as atherosclerosis. The ethological studies on stenosis suggest that deposition of calcium, fatty components and cholesterol on the inner walls of the artery prevent the flowing of blood leading to rupture of the artery and thrombosis. Since the experimental study of blood flow in stenosed artery has some limitations such as the setting of a small tube with constriction and the ethical reason of using human blood, the study of blood flow via mathematical model can be a good alternative to understand the behavior of blood flow.
A lot of work has been done in relation to the development of sclerosis, where in the majority of the studies, shape of the stenosis was considered to be either symmetric or asymmetric. But it is understood that the stenosis may be multiple in nature or develop in an irregular manner. The geometry of stenosis may be complicated base on each individual patient. From the previous studies, we can classify the model into three groups based on mathematical expression such as exponential shape or bell shape stenosis, cosine shape and polynomial shape. Mathematical modeling and analysis of an artery with multiple stenoses is of great use for medical Scientists and Biomathematicians because it involves the investigation of various characteristics of blood. The mathematical modelling and numerical simulation studies have the huge potential and can very well interpret existing in vivo data and eventually help in the improved diagnosis.
A number of studies related to blood flow through stenosed arteries have been carried out. During the past few decay several studies were conducted in this direction of several fluid and blood flow problems. Lykoudis and Roos studied the mechanics of the duct with an inserted catheter by considering a moving peristaltic wave on the stationary cylinder [4]. Smith studied the flow through constricted tube and analyzed the impact of mild, moderate, and severe stenoses on totally developed flow [5]. He developed mathematical model for understanding the dynamics of blood flow in an exceedingly constricted artery. Author discussed steady and pulsatile nature of polar fluid through asymmetric tapered artery. Here they have given a table showing the locations of the maximum height of the stenosis and the corresponding annular radius for various values of the tapered and shape parameter. Had conveyed the mathematical description for blood flow inside a diseased artery by using a catheter. They had considered different shapes of stenosis in their theoretical investigation. In 2000, S. Chakravarty and P. K. Mandal studied the Newtonian flow in stenosed arteries [6]. The stenosis is considered in timevariant, overlapping and tapered artery. The Navier-Strokes equation and equation of continuity are solved using Runge-Kutta method. They concluded that the present of tapering angle greatly reduce the axial velocity. In 2019 Liu and Liu studied the K-L model of blood flow though bell-shaped stenosis arteries [7].
The shapes of the stenosis in the above aforesaid studies have been considered to be radially symmetric or asymmetric. But while stenosis is maturing it may grow up in series manner, overlap with each other and it would be appear like x-shape observed the pressure gradient force, flow velocity, impedance and wall shear stress in the overlapping stenotic zone at the critical height and at the throats of such stenosis. Here they considered steady nature of flow [8]. Srivastava et al. explored the arterial blood flow through an overlapping stenosis by treating the blood as a Casson fluid [9]. Stenosis increases the resistance to the flow of blood in arteries resulting in increased blood pressure. It is now a well-established fact that stenosis induces substantial changes in blood flow velocity, pressure distribution, wall shear stress and impedance. The assumptions of blood flow parameters made from mathematical modelling can be crucial and lifesaving. In this paper we try to model the blood flow in stenosed artery to understand the behavior of blood and connect it to the possible leading medical condition. The heat transfer phenomenon also has significant importance in fluid flow problems. Bhatti et al. [10] had interpreted the heat transfer of blood flow inside a diseased artery having a thrombus. In 2015, developed a mathematical model of unsteady polar fluid in w-shaped stensed artery and analyzed various result in the resistance to the flow and wall shear stress with respect to stenosis size, radius of the catheter, couple stress fluid parameters, Reynolds number and pulsatile parameter but not observed any result regarding temperature distribution. In this paper, we have only discussed the temperature distribution in whapped stenosed artery.
We have done this work because in several investigations the velocity profile, resistance to flow, shear stress etc. has been discussed but the temperature profile has never been discussed for w-sahped stenosed artery. So in this work we have aimed to understand the effects of heat transfer phenomenon on the Prandalt fluid model through a w-shaped stenosed atherosclerotic artery. The convection of heat transfer with a catheterized mild stenotic artery with a clot has been taken into consideration. And the nonlinear coupled equations are solved exactly under mild stenotic conditions using the geometry for a mild stenotic artery in the presence of a clot. The heat and mass transfer phenomenon was discussed with distinct values of the temperature profile for some distinct values of flow parameters using graphs. As of now, this model has not been discussed for this kind of blood flow problem. Due to lesser attention by researchers, this area has not been studied much but, on the other hand, medical application problems regarding non-Newtonian fluids are widely involved.
Mathematical formulation
Mathematical model of blood flow through an w-shaped stenosed arterial segment through a tapered artery in the presence of catheter is to be built to study the impact of various geometric and fluid parameters on physiological parameters. This present study aims to examine an nanoparticles in blood flow with a constant viscosity μ and density ρ in two coaxial tubes with length L; the inner tube contains a clot on its wall and the outer tube contains an axially symmetric mild stenosis. The cylindrical coordinate system (r, θ, and z) is chosen such than u and we are the velocity components in the r and directions, respectively. Mixed convection is used to calculate the heat transfer by assigning the temperature T0 to the wall of the tube. The geometry of the w-shaped stenosis in the outer tube and clot in the inner tube is shown in Figure 1 and is expressed mathematically with inputs from Srikanth et al. [11] (Figure 1).
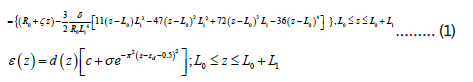
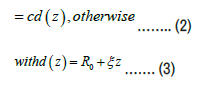
In the above equations, d (z) is the radius of the tapered arterial segment in the stenotic region, where R0 is the radius of the annular region in case of non-tapered artery in the no constricted domain, Rc is the radius of the catheter, L1 is the stenosis length, L0 indicates the location of stenosis, _ is the maximum height of the stenosis into the umen, ξ (= tanφ ) the tapering parameter which represents the slope of the tapered vessel with ϴ being the tapering angle. φ < 0; φ > 0 and φ =0 are for converging taper, diverging taper and no-taper respectively. z1 and z3 are the left and right locations on the axial line where the maximum height of the stenosis is occurring and z2 represents the location on z axis corresponding to the critical height of the w-shaped stenosis and n ≥ 2 is the parameter determining the shape of the constriction profile and referred to as the shape parameter, and k is given by:
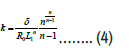
where δ is the maximum height of the stenosis located at,
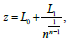
σ is the maximum height attained by the clot at z=zd+0.5, c d(z) is the radius of the inner tube, and c<<1 and zd is the axial displacement of the clot as shown in Figure 1.
The constitutive equations for the prandalt fluid model are given Akbar et al. [12]
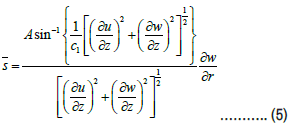
Governing equation
The equations for incompressible nano particles in blood flow in the presence of body forces are given by
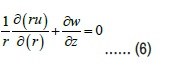
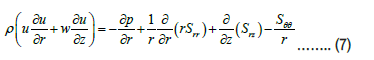
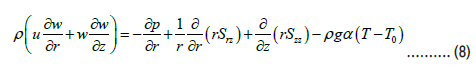
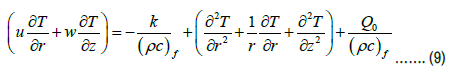
In the presented equations, p is the fluid pressure, μ is the viscosity of the base fluid, g is gravity, and Q0 is the constant heat absorption or heat generation. To solve the governing equations, we introduce the following dimensionless parameters
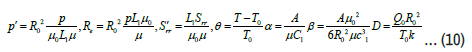
where u0 is the average velocity over the section of the channel, A and C1 are material constants for Prandalt fluid model, D is the dimensionless heat source or sinks parameter with the fluid, and Gr is the Grash of number. Using the above non-dimensional parameters along with the additional conditions.
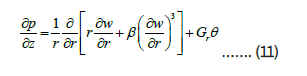
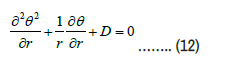
Boundary condition
θ =0, at r =h (z), θ =1 at r =(z) ………. (13)
Further, we consider three types of arteries, converging tapering (φ < 0), non-tapering (φ = 0), and diverging tapering arteries (φ > 0). The temperature profile is obtained by evaluating, subject to corresponding boundary conditions given.
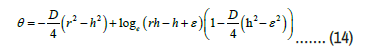
For the purpose of observation the desired quantities of major physiological significance, the following parameters values have been made use of k=0.00001, zd=0.6 Q=0.05, C=0.05 To=25°C Rc=0.1 and the location of the extremum heights of the stenosis (z1; z2; z3) and the corresponding radius of the annular region for various values of the tapered parameter ξ are numerically calculated with fixed values of L = 2;R0 =1, L1 = L/2, L0= (L -L1)/2 summarized.
During the formulation and solution, the locations on the axial axis corresponding to the maximum height of the stenosis which are dependent on the tapered parameter. The Figures display the graphical representations of temperature distribution versus radial distance and height of stenosis for different parameters. In this section we discuss only the results of temperature profile with effect of maximum height of the clot (σ), maximum height of the stenosis ( δ ) the tapered parameter ( ξ ).The objective of this analysis is to study the change in temperaure pattern and estimate the variation in (maximum height of the stenosis) (tapering angle) in a w-shaped stenosed tapered artery when a catheter is inserted into it. From Figures 2 and 3 it is depicted that the temperature slightly increase with increasing value of σ i.e. maximum height of the clot and the temperature decline with increase values of i.e. maximum height of the stenosis. It is also observed when the height of blood clot (σ), increase then the temperature of blood flow increases with wall having clot but it remain almost same with the stenosed wall. It is observed from Figures 2 (a-c) that temperature for different value of h (z) for w-shaped stenosis in narrow region and passes in h (z2, z3) when region is slightly wide than temperature increases in w-shaped stenosis artery for all cases (Figures 2a-2c and 3a-3c).
From Figures 2(c) and 3 (c), on increasing value of σ (maximum height of the clot)= 0.4 the temperature profile for w-shaped stenosed artery for h (z1), h (z2) and h (z3) very interesting result come out that when it comes in constricted region than take the flow like loop and after σ=0.4 its decrease continuously for all cases. The main aim of this mathematical study is to explore the heat transfer phenomena of blood flow through a tapered stenosed artery along with the clot with the flow of blood using the Prandalt fluid model. These figures also show that an increase in the value of the maximum height attained by the clot (σ) and the maximum height attained by the stenosis ( δ ) will result in an increase in the amount of heat generated. An increase in the amount of heat generated will raise the blood pressure inside the artery. Higher blood pressure has a strong possibility of creating extra pressure that could make the artery burst. Also in a narrow artery, the risk of being blocked is greater.
Figure 3a. Temperature (ϴ) for distinct values of h(z) for stenosis height (* ) =0.3. 
Figure 3b. Temperature (ϴ) for distinct values of h (z) for stenosis height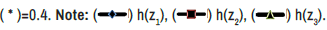
Figure 3c. Temperature (ϴ) for distinct values of h (z) of stenosis height (* )=0.5.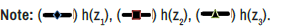
Figure 4 also depicts how the non-tapered, diverging tapering, and converging tapering arteries affect the temperature profile (θ) with a radius of artery and stenosis h (z) for distinct values of tapering angles (φ). It is seen that the Figure 4 for a decrease in the tapering angle the temperature profile decrease after at the r=0.4 and slightly increase at r=0.8 for the different value of h(z) due to w-shaped stenosed artery and also see that on variation of h (z), the temperature profile along tapering angle has insignificant effect. It is shown that, for the case of converging tapering, the temperature gives greater values as compared to the case of diverging tapering. And it is observed that the temperature rises in the case of non-tapered [13-15] (Figure 4).
In conclusion, the study highlights the complexity of arterial stenosis and its implications for blood flow dynamics and heat transfer. While previous research has largely focused on symmetric or asymmetric stenosis shapes, this study addresses the need to consider irregular, x-shaped stenosis formations. By modeling blood flow through w-shaped stenosed arteries and examining temperature distribution, valuable insights into physiological conditions and medical diagnoses are gained. The findings underscore the importance of considering heat transfer phenomena in fluid flow problems, especially in the context of non-Newtonian fluids and cardiovascular health.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
Journal of Blood & Lymph received 443 citations as per Google Scholar report