Research - (2022) Volume 10, Issue 1
Received: 01-Jan-2022, Manuscript No. economics-22-53162;
Editor assigned: 03-Jan-2022, Pre QC No. P- 53162;
Reviewed: 14-Jan-2022, QC No. Q- 56162;
Revised: 20-Jan-2022, Manuscript No. R-53162;
Published:
28-Jan-2022
, DOI: 10.37421/2375-4389.22.10.391
Citation: Siregar, Dodi Irwan. The Appropriate of the COVID-19 Vaccine by Analysing the Death Rate/Mortality Corona Virus-19 and Confirmed the Corona Virus-19 in World during December 2020 until September 2021.Economics 10 (2022): 391.
DOI: 10.37421/2375-4389.22.10.391
Copyright: © 2022 Siregar DI. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abst Viruses are important pathogens of high animals and the major cause of mortality, and they also are drivers of global geochemical cycles; yet, biological sciences considered them as entities separate from the realm of life and acting merely as mechanical artifacts that can exchange genes between different species, genera, phyla and even from one ecosystem to another. During the last decade, the increased awareness of the complexity of the immune system and its determinants, including at the host genetic level, indicated that using system biology approaches to assess how various processes and networks interact in response to immunization could prove more illustrative than trying to isolate and characterize a few components of vaccine responses. These immune-related concerns have largely spread into the population, and questions related to the immunological safety of vaccines that is, their capacity for triggering 2 non-antigen specific responses possibly leading to allergy, autoimmunity, or even premature death are being raised. Certain “off-targets effects” of vaccines have also been recognized and call for studies to quantify their impact and identify the mechanisms at play. This study uses multiple linear regression analysis to predict and predict changes in the value of certain variables when other variables change. Correlation is one of the statistical analysis techniques used to find the relationship of how strong the relationship between two or more variables that are quantitative. By using the Linearity Test (Lillie force test) where f count > f table is 787,62 > 3,24Then, Ho is rejected. This means that multiple linear regression analysis can be used to predict The Corona virus 19 vaccines in world by analyzing Variable The death rate and confirmed the corona virus 19 data. Obtained the multiple linear regression equation is Y = 0,609211 - 3,15845257X1 + 3,58359X2, the correlation value of the variables above is 0,98389 the value is superior correlation scale ranging from 0.76 to 0.99. Is where t1 count < t table is -12,078 < 2,009, then Ho is accepted, meaning there is no significant effect partially between the Variable The Corona virus 19 vaccine and The death rate. Then the value of the t2 count > t table is 3,62523 > 2,009. Ho is rejected; it means that there is a large significant influence partially between the Corona virus 19 vaccines against confirmed the corona virus 19 variable in World on August 2021.
The Corona virus 19 vaccine • The death rate • Confirmed the corona virus 19 • Country of World • Multiple linear regression Correlations
To generate vaccine-mediated protection is a complex challenge. Currently available vaccines have largely been developed empirically, with little or no understanding of how they activate the immune system. Their early protective efficacy is primarily conferred by the induction of antigen-specific anti bodies. However, there is more to antibody mediated protection than the peak of vaccine-induced antibody titers. The quality of such antibodies (e.g., their avidity, specificity, or neutralizing capacity) has been identified as a determining factor in efficacy. Long-term protection requires the persistence of vaccine antibodies above protective thresholds and/or the maintenance of immune memory cells capable of rapid and effective reactivation with subsequent microbial exposure. The determinants of immune memory induction, as well as the relative contribution of persisting antibodies and of immune memory to protection against specific diseases, are essential parameters of long-term vaccine efficacy. The predominant role of B cells in the efficacy of current vaccines should not overshadow the importance of T-cell responses: T cells are essential to the induction of high-affinity antibodies and immune memory, directly contribute to the protection conferred by current vaccines such as Bacille Calmette-Guérin (BCG), may play a more critical role than previously anticipated for specific diseases like pertussis, and will be the prime effectors against novel vaccine targets with predominant intracellular localization such as tuberculosis. New methods have emerged allowing the assessment of a growing number of vaccine-associated immune parameters, including in humans. This development raises new questions about the optimal markers to assess and their correlation with vaccine induced protection. The identification of mechanistic immune correlates or at least surrogates of vaccine efficacy is a major asset for the development of new vaccines or the optimization of immunization strategies using available vaccines. Thus, their determination generates a considerable amount of interest. During the last decade, the increased awareness of the complexity of the immune system and its determinants, including at the host genetic level, indicated that using system biology approaches to assess how various processes and networks interact in response to immunization could prove more illustrative than trying to isolate and characterize a few components of vaccine responses [1]. Delineating the specific molecular signatures of vaccine immunogenicity is beginning to highlight novel correlates of protective immunity and better explain the heterogeneity of vaccine responses in a population. The tailoring of vaccine strategies for specific vulnerable populations, including very young, elderly, and immunosuppressed populations, also largely relies on a better understanding of what supports or limits vaccine efficacy under special circumstances at the population and individual levels. Lastly, the exponential development of new vaccines raises many questions that are not limited to the targeted diseases and the potential impacts of their prevention, but that address the specific and nonspecific impacts of such vaccines on the immune system and, thus, on health in general. These immune-related concerns have largely spread into the population, and questions related to the immunological safety of vaccines that is, their capacity for triggering 2 non– antigen-specific responses possibly leading to allergy, autoimmunity, or even premature death are being raised [2]. Certain “off-targets effects” of vaccines have also been recognized and call for studies to quantify their impact and identify the mechanisms at play. The objective of this chapter is to extract from the complex and rapidly evolving Feld of immunology the main concepts that are useful to better address these important questions [3].
Populations and samples
Definition population is the set of all the individuals of interest in a particular study. Although research question concerns an entire population, it usually is impossible for a researcher to examine every single individual in the population of interest. Therefore, researchers typically select a smaller, more manageable group from the population and their studies to the individuals in the selected group. In the statistical terms a set of individuals selected from a population is called a sample. A sample intended to be representative of its population, a sample should always be identified in terms of the populations from which it was selected. Definition A sample is a set of individuals selected from a population, usually intended to represent the population in a research study.
Collecting data
Once you decide on the type of data – quantitative or qualitative – appropriate for the problem at hand, you will need to collect the data. Generally, you can obtain data in four different ways:
1. Data from a published source
2. Data from a designed experiment
3. Data from a survey
4. Data collected observationally
Sometimes, the data set of interest has already been collected for you and is available in a published source, such as a book, journal, or newspaper. For example, you may want to examine and summarize the divorce rates (i.e., number of divorces per 1,000 populations) in the 50 states of the World. You can find this data set (as well as numerous other data sets) at your library in the statistical abstract of the World, published annually by the U.S. government.
The independent and dependent variables
Definitions the independent variable is the variable that is manipulated by the researcher. In behavioral research, the independent variable usually consists of the two (or more) treatment conditions to which subjects are exposed. The independent variable consists of the antecedent conditions that were manipulated prior to observing the dependent variable. The dependent variable is the one that is observed for changes in order to assess the effect of the treatment (Table 2).
A comment on stating null and alternative hypothesis
A statistical test procedure cannot prove the truth of a null hypothesis. When we fail to reject a null hypothesis, all the hypothesis test can establish is that the information in a simple of data is compatible with the null hypothesis. On the other hand, a statistical test can lead us to reject the null hypothesis, with only a small probability, α, of rejecting the null hypothesis when it is actually true. Thus rejecting a null hypothesis is stronger conclusion than failing to reject it. The null hypothesis is usually stated in such stated in such a way that if our theory is correct, then we will reject the null hypothesis. For example, our airplane seat designer has been operating under the assumption (the maintained or null hypothesis) that the population means hip width is 16.5 inches. Casual observation suggests that people are getting larger all the time. If we are larger and if the airplane wants to continue to accommodate the same percentage of the population, then the seat width must be increased.
This costly change should be undertaken only if there is statistical evidence that the population hip size indeed larger. When using a hypothesis test we would like to find out whether there is statistical evidence against our current “theory,” or whether the data are compatible with it. With this goal, we set up the null hypothesis that the population mean is 16.5inches, H0: μ = 16.5, against the alternative that have shown that there has been a “statistically significant” increase in hip width. You may view the null hypothesis to be too limited in this case, since it is feasible that the population mean hip width is now smaller than 16.5 inches. The hypothesis test of the null hypothesis Ho: μ ≤ 16.5 against the alternative hypothesis H1: μ >16.5 is exactly the same as the test for Ho: μ = 16.5 against the alternative hypothesis H1: μ = 16.5 against the alternative hypothesis H1 >μ = 16.5. The test statistic and rejection region are exactly the same. For a one-tail test you can form the null hypothesis in either of these ways. Finally, it is important to set up the null and alternative hypotheses before you analyse or oven collects the sample of data. Failing to do so can lead to errors in formulating the alternative hypothesis. Suppose that we wish to test whether μ >16.5 and the sample mean is ŷ = 15.5. Does that mean we should set up the alternative μ< 16.5, to be consistent with estimate? The answer is no, the alternative is formed to state the conjecture that we wish to establish, μ >16.5.
Relating two measurement: Regression
This chapter considers relationships between two measurements that can be represented by a line. Such relationships are called linear and their models are called regression models. As usual, we deal with settings in which there is variability in measurement. Observations in different circumstances but with the same x may give different values of y. Perhaps the true line goes through the first value of y and perhaps it goes through the second – more likely, it goes through neither [4]. Despite there being strength in numbers, any finite sample gives less than perfect information about the line. Since anything uncertain has a probability distribution, the line itself has a probability distribution. Lines are specified by slopes and intercepts and so probabilities for lines are specified by probabilities for b and α. A major focus of this section is on the slope, b, because it indicates the degree of the relationship between x and y: increasing x by 1 unit means increasing y by b units. In particular, b = 0 means there is no relationship between x and y, at least not a linear relationship [5].
The regression effect arises in every aspect of life and yet few people appreciate its existence. As a result, some people mistakenly attribute change to an ineffective intervention. A golfer has a terrible round and then takes a lesson – she does better the next time and praises her teacher. A baseball player is in a slump and changes bats – the next day he gets two hits and credits the bat. A woman a backache goes to a specialist and her backache improves – she thinks the specialist is a genius. A man is feeling depressed and goes to psychiatrist may be effective. But another explanation is possible and even likely in all this cases: the regression effect, also called regression to the mean. It is simple and ubiquitous: there are ups and downs in any sequence of exchangeable observation; drops tend to follow the ups and rises tend to follow the downs [5].
The first recorded observation of the regression effect was by Francis Galton. He found that seeds of mother sweet pea plants that happen to be larger than average tend to have daughters that are larger than average tend to have daughters that are smaller than average – but larger than themselves. The comparison from one generable to the next is a reversion or regression to the mean. Similarly, Galton noticed that sons of short men tend to be short – but not as short as their fathers. (Imagine what would happen to the population if the opposite were true and tall men tended to have sons taller than themselves and short men tended to have sons shorter than themselves!). Sports statistics that show the regression effect are readily [6].
The correlational method
Definition with the correlation method, two variables are observed to see if there is a relationship. The simplest way to look for relationship between variables is to make observations of two variables as they exist naturally. This is called the observational or correlation method.
Parameters in statistics
Definition parameters in statistics a value, usually a numerical value, that describes a population. A parameter may be obtained from a single measurement, or it may be derived from a set measurement from the population. A statistic is a value, usually a numerical value, that describes a sample. A statistic may be obtained from a single a measurement, or it may be derived from a set of measurement from the sample. We examine the relationship between the mean obtained for a sample and the mean for the population from which the sample was obtained.
Multiple regression analysis
Multiple regression analysis is a statistical technique that can be used to analyze the relationship between a single dependent (creation) variable and several independent variables. The objective of multiple regression analysis is to use the independent variables whose values are known to predict the single dependent value selected by the researcher. Each independent variable is weighted by the regression analysis procedure to ensure maximal prediction from the set of independent variable. The weights denote the relative contribution of the independent variables to the overall prediction and facilitate interpretation as to the influence of each variable in making the prediction, although correlation among the independent variables complicates the interpretative process. The set of weighted independent variables forms the regression variety, a linear combination of the independent variables that best predicts the dependent variable. The regression variety, also referred to as the regression equation or regression equation or regression model, is the most widely known example of vitiate among the multivariate techniques. Multiple regression analysis is a dependence technique. Thus, to use it you must be able to divide the variables into dependent and independent variables. Regression analysis is also a statistical tool that should be used only when both the dependent and independent variable are metric. However, under certain circumstances it is possible to include non-metric data either as independent variables (by transforming either ordinal or nominal data with dummy variable coding) or dependent variable. In summary, to apply multiple regression analysis: (1) the data must be metric or appropriately transformed, and (2) before deriving the regression equation, the researcher must decide which variable is to be dependent and which remaining variables will be independent [7]. Term used to express the concept that the model processes the properties of additives and homogeneity. In a simple sense, linear models predict values that falls a straight line by having a constant unit change (slope) of the dependent variable for a constant unit change of the independent variable. In the population models, Y = b0 + b1X1+ , the effect of a change of 1 in X1 is to add b1 (a constant) units of Y [8].
Although there are many problems in which one variable can be predicted quite accurately in terms of another, it stands to reason that predictions should improve if one considers additional relevant information. For instance, we should be able to make better predictions of the performance of newly hired teachers if we consider not only their education, but also their years of experience and their personality. Also, we should be able to make better predictions of new textbook’s success if we consider not only the quality of the work, but also the potential demand and the competition.
Although there are many different formulas that can be used to express regression relationships among than two variables, most widely used are linear equations of the form;
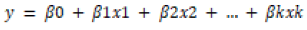
This is partly a matter of mathematical convenience and partly due to the fact that many relationships are actually of this form or can be approximated closely by linear equations. In the equations above, Y is the random variable whose values we want to predict in terms of given values of x1, x2, … , and xk, and β0, β1, β2, … , and βk, the multiple regression coefficients, are numerical constants that must be determined from observed data, [9]. For each variable, the value of observations from one another, is not related. Multiple correlation is a correlation consisting of two independent variables (X1, X2) or more, and one dependent variable (Y). the relationship between variables can be described as follows:
Transformation data
Transforms are usually applied so that the data appear to more closely meet the assumptions of a statistical inference procedure that is to be applied, or to improve the interpretability or appearance of graphs. Nearly always, the function that is used to transform the data is invertible, and generally is continuous. The transformation is usually applied to a collection of comparable measurements. For example, if we are working with data on peoples' incomes in some currency unit, it would be common to transform each person's income value by the logarithm function.
Partial F (or t) values
The partial F-test is simply a statistical test for the additional contribution to prediction accuracy of a variable above that of the variables already in the equation. When a variable (Xα) is added to a regression equation after other variables are already in the equation, its contribution may be very small even though it has a high correlation with the dependent variable. The reason is that Xα is highly correlated with the variables already in the equation. The partial F value is calculated for all variables by simply pretending that each variable above all others in the equation indicates its low or insignificant partial F value for a variable not in the equation indicates its low or insignificant contribution to the model as already specified. A t value being approximately the square root of the f value [10].
Partial F values
As discussed earlier, two computational approaches – simultaneous and stepwise can be utilized in deriving discriminate functions. When the stepwise method is selected, an additional means of interpreting the relative discriminate power of the independent variables is available through the use of partial F values. This is accomplished by examining the absolute sizes of the significant F values and ranking them. Large F values indicate greater discriminatory power. In practice, rankings using the F-values approach are the same as the ranking derived from using discriminate weight, but the F values indicate the associated level of significance for each variable [11]
To test the hypothesis that the amount of variation explained by the regression model is more than the variation explained by the average, the F table is used. The test statistic F table is calculated as:
Where,
F tab= (SSE regression/df regression)/(SSE total/df residual)
df regression = number of estimated coefficient (Including intercept) – 1
df residual = sample size – number of estimated coefficient (including intercept).
The t-test
The t test assesses the statistical significance of the difference between two independent sample means. If the t value is sufficiently large, then statistically we can say that the difference was not due to sampling variability, but represents a true difference. This is done by comparing the t statistic to the critical value of the t statistic (tcrit). If the absolute value of the statistic is greater than the critical value, this leads to rejection of the null hypothesis of no difference in the appeals of the advertising messages between groups. This means that the actual difference due to the appeals is statistically larger than the difference expected from sampling error. We determine the critical value (tcric) for our t statistic and test the statistical significance of the observed differences by the following procedure:
1. Compute the t statistic as the table of the difference between samples to the standard error.
2. Specify a type I error level (denoted as α, or significance level), which indicates the probability level the researcher will accept in concluding that the group means are difference when in fact they are not.
3. Determine the critical value (tcrec) by referring to the distribution with N1 + N2 – 2 degrees of freedom and specified α, where N1 and N2 are samples size.
If the absolute value of the computed t statistic exceeds tcrit, the researcher can conclude that the two advertising messages have different levels of appeal (i.e., μ1 ≠ μ2), with a type I error probability of α. The researcher can then examine the actual mean values to determine which group is higher on the dependent value [12].
Correlation coefficient (r)
Another measure of the relationship between two variables is the correlation coefficient. This section describes the simple linear correlation, for short linear correlation, which measures the strength of the linear association between two variables. In other words, the linear correlation coefficient measures how closely the points in a scatter diagram are spread around regression line. The correlation Calculated for population data is denoted by (Greek letter rho) and the one calculated for sample data is, denoted by r. (Note that the square of the correlation coefficient is equal to the of determination) [13]. Coefficient that indicates the strength of the association between any two metric variables. The sign (+ or -) indicates the direction of the relationship. The value can range from -1 to +1, with +1 indicating a perfect positive relationship, 0 indicating no relationship, and -1 indicating a perfect negative or reverse relationship (as one variable grows larger, the other variable grows smaller) [14].
The coefficient of correlation (r) is simply the square root of the coefficient of determination (r2). Thus, four our, the coefficient of correlation is r = √r2 = √.982 = .991. As you can see, r is a positive value in this case, but r can also be negative. The algebraic sign for r is always the same as that of b in the regression equation. The coefficient of correlation isn’t as useful as the coefficient of determination, since it’s an abstract decimal and isn’t subject to precise interpretation. (As the square root of a percentage, it cannot itself be interpreted in percentage terms). But r does provide a scale against which the closeness of the relationship between -1.00 and +1.00. When r is zero, there is no correlation, and when r = -1.00 or +1.00, there is perfect correlation. Thus, the closer r is to its limit of ± 1.00, the better the correlation, and the closer it is zero, the poorer the relationship between the variables
Null hypothesis and alternative hypothesis for f-test
Null Hypothesis (Ho) that is, linear regression analysis cannot be used in analysing the death rate/Mortality (X1) and confirmed the corona virus 19 (X2) on The COVID-19 vaccine (Y).
Alternative Hypothesis (Hα) that is, linear regression analysis can be used in analysing the death rate/Mortality (X1) and confirmed the corona virus 19 (X2) on The COVID-19 vaccine (Y).
The F-test
The partial F-test is simply a statistical test for the additional contribution to prediction accuracy of a variable above that of the variables already in the equation. When a variable (Xα) is added to a regression equation after other variables are already in the equation, its contribution may be very small even though it has a high correlation with the dependent variable. F value is 787,62 and F table is 3,183. F value > F table is 787,62 >3,24 Then, Ho is rejected. So, multiple linear regression analysis can be used in analyzing the death rate/Mortality (X1) and confirmed the corona virus 19 (X2) on The COVID-19 vaccine (Y).
Multiple regression analysis
Although there are many different formulas that can be used to express regression relationships among than two variables, most widely used are linear equations of the form;
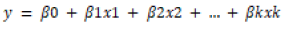 The results of multiple
linear regression analysis obtained the equation The COVID-19 vaccine (Y)
by analyzing the death rate/Mortality corona virus 19 as (X1) to The COVID-19
confirmed (X2) we get the formula for multiple linear regression equation as
follows:
The results of multiple
linear regression analysis obtained the equation The COVID-19 vaccine (Y)
by analyzing the death rate/Mortality corona virus 19 as (X1) to The COVID-19
confirmed (X2) we get the formula for multiple linear regression equation as
follows:
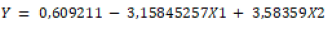 By using the above equation we can predict or predict Life Expectancy in World in the future by
using these multiple linear regression equations.
By using the above equation we can predict or predict Life Expectancy in World in the future by
using these multiple linear regression equations.
Correlation coefficient (r), partial correlation coefficient
Value that measures the strength of the relationship between the criterion or independent variable and a single independent variable when the effects of another independent variables in the model are held constant. For example, ry,x2,x1, measures the variation in Y associated with X2, when the effect of X1 on both X2 and Y is held constant. This value is used in sequential variable selection methods of regression model estimation to identify the independent variable with the greatest incremental predictive power beyond the independent variables already in the regression model [15,16]. Value that measures the strength of the relationship between the criterion or independent variable and a single independent variable when the effects of another independent variables in the model are held constant. For ry,x2,x1, measures the variation in Y associated with X2, when the effect of X1 on both X2 and Y is held constant. The value of ry,x2,x1 is 0,983892 with the interpretation being Superior Correlation which ranges from 0.75 to 0.99. For ry,x1, measures the variation in Y associated with X1. The value ry,x1 is 0.98886 with the interpretation being doubtful Correlation, which ranges from 0.00 to 0.25. For ry,x2 measures the variation in Y associated with X2. The value ry,x2 is 0.9906 with the interpretation being superior Correlation, which ranges from 0.76 to 0.99. For rx1,x2 measures the variation in X1 associated with X2. The value of rx1,x2 is 0.99968 with the interpretation being, superior Correlation, which ranges from 0.76 to 0.99 (Table 1 and 2).
| Value of Correlation (r) | Interpretation (r) |
|---|---|
| 0.00 – 0.25 | Doubtful correlation |
| 0.26 – 0.50 | Fair correlation |
| 0.51 – 0.75 | Good correlation |
| 0.76 – 1.00 | Superior correlation |
| Date’s | The Death Rate/Mortality Corona Virus 19 (X1) |
Confirmed the Corona Virus 19 (X2) | The COVID-19 vaccine (Y) |
|---|---|---|---|
| 04 Jan 21 | 79,686 | 5000868 | 3940793 |
| 11 Jan21 | 89,192 | 4828430 | 18725297 |
| 18 Jan 21 | 97,667 | 4244093 | 27041142 |
| 25 Jan 21 | 1,00,994 | 3760012 | 45043901 |
| 01 Feb 21 | 1,01,074 | 3221158 | 61855273 |
| 8 Feb21 | 92,656 | 2730732 | 79226560 |
| 15 Feb 21 | 85,194 | 2480313 | 101939133 |
| 22 Feb 21 | 71,086 | 2663764 | 125494108 |
| 8 Mar 21 | 66,300 | 2961331 | 189905011 |
| 15 Mar 21 | 62,904 | 3308464 | 152024730 |
| 22Ma r21 | 61672 | 3819085 | 230804904 |
| 29 Mar 21 | 63,835 | 4060642 | 277430192 |
| 05 Apr 21 | 69,952 | 4559259 | 327306417 |
| 12 Apr 21 | 74,037 | 5238407 | 385434619 |
| 19 Apr 21 | 79,986 | 5704421 | 455196888 |
| 26 Apr 21 | 87,221 | 5703313 | 515167425 |
| 03 May 21 | 91,414 | 5476552 | 567179728 |
| 10 May 21 | 96,727 | 4817080 | 615591070 |
| 17 May 21 | 93,310 | 4207261 | 665800483 |
| 24 May 21 | 88,499 | 3563568 | 718770886 |
| 31 May 21 | 86,954 | 3031537 | 780273491 |
| 07 Jun 21 | 80,330 | 2667666 | 848323546 |
| 14 Jun21 | 74,119 | 2548662 | 921757497 |
| 21 Jun 21 | 73,526 | 2612568 | 1627054655 |
| 28 Jun 22 | 64,842 | 2726659 | 1732610327 |
| 05 Jul 21 | 58,554 | 3075287 | 1732610327 |
| 12 Jul 21 | 54,584 | 3534912 | 2185505175 |
| 19 Jul 21 | 56,372 | 3909772 | 1913584923 |
| 22 Jul 21 | 57,229 | 4118176 | 1994376343 |
| 26 Jul 21 | 69,912 | 4329532 | 2078422978 |
| 2 Aug 21 | 64,290 | 4505310 | 2078422978 |
| 9 Aug 21 | 66,127 | 4559238 | 2158464818 |
| 16 Aug 21 | 67,388 | 4426234 | 2551033733 |
| 23 Aug 21 | 68,816 | 4509113 | 2362262658 |
| 30 Aug 21 | 68,274 | 3999873 | 2466849992 |
| 6 Sep 21 | 67,655 | 3760926 | 2550595141 |
| 13 Sep 21 | 64,025 | 3075287 | 3110927999 |
| Σ | 2,85,8421 | 14,73,74,742 | 41881576167 |
Hypothesis for t-test Partial influence test (t-test) between X1 and Y
Null Hypothesis (Ho) that is, there is no significant (very large) effect partially between The death rate/Mortality corona virus 19 as variable X1 on The COVID-19 vaccine as Y. Alternative Hypothesis (Hα) that is, there is a significant (very large) effect partially between The death rate/Mortality corona virus 19 as variable X1 to The COVID-19 vaccine as Y.
t1 value is - 12,078 and t table is 2,015. So, t1 value < t table is the value of - 12,078 < 2,015; then Ho is accepted meaning, there is no significant (very large) effect partially between The death rate/Mortality corona virus 19 as variable X1 to The COVID-19 vaccine as Y.
Partial influence test (t-test) between X2 and Y
Null Hypothesis (Ho) that is, there is no significant (very large) effect partially between The death rate/Mortality corona virus 19 (X1) in World(X2) on The COVID-19 vaccine in World (Y).
Alternative Hypothesis (Hα), that is, there is a significant (very large) partial effect between The death rate/Mortality corona virus 19 (X1) in World (X2) on The COVID-19 vaccine in World (Y).
t2 value is 3,62523 and t table is 2,009. So, for t2 value > t table that is 3,62523 > 2,009 then Ho is rejected meaning, there is significant/big correlation partial effect between The death rate/Mortality corona virus 19 (X2) on The COVID-19 vaccine (Y) from Desember 2020 until September 2021 (Figures 1-3) .
From the results of the study it can be concluded as follows: F value > F table that is 787,62 > 3,24 Then, Ho is rejected that is, linear regression analysis can be used in analyzing the influence of the dependent variable (free) Fossil value of fuel energy consumption (% of total) and confirmed the corona virus 19 on the independent variable (dependent) The COVID-19 vaccine. The multiple linear regression equation of these variables is as follows.
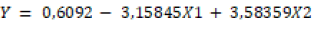 Correlation (interrelation)
of variables in multiple linear regression (ry,x1,x2) that is, independent
variable (free); The COVID-19 vaccine is variable (Y) of the dependent variable
(free) Fossil value of fuel energy consumption (% of total) (X1) and Confirmed
the corona virus 19 (X2) obtained results (ry,x1,x2 is 0,983892) with interpretation
is superior correlation which ranges from 0.75 to 0.99. For t₁ value < t
table; that is -12,078 < 2,015, so, Ho is accepted, that is a significant (large)
relationship between The COVID-19 vaccine with the death rate/mortality corona
virus 19. For t2 value > t-table that is 3,6252 > 2,015, then Ho is rejected,
it means, there is a no significant/close relationship between The COVID-19
vaccine with Confirmed the corona virus 19.
Correlation (interrelation)
of variables in multiple linear regression (ry,x1,x2) that is, independent
variable (free); The COVID-19 vaccine is variable (Y) of the dependent variable
(free) Fossil value of fuel energy consumption (% of total) (X1) and Confirmed
the corona virus 19 (X2) obtained results (ry,x1,x2 is 0,983892) with interpretation
is superior correlation which ranges from 0.75 to 0.99. For t₁ value < t
table; that is -12,078 < 2,015, so, Ho is accepted, that is a significant (large)
relationship between The COVID-19 vaccine with the death rate/mortality corona
virus 19. For t2 value > t-table that is 3,6252 > 2,015, then Ho is rejected,
it means, there is a no significant/close relationship between The COVID-19
vaccine with Confirmed the corona virus 19.
Without reservation, we would like to thank you to my parents, my father; Misran Siregar and my Mother; YurnitaYunus, and thank you to reviewers and the seminar participants at Persada University in Pekanbaru for their helpful comments and suggestions, as well as the World Development Indicators “World Bank Data”. The views expressed in this paper are those of the authors.
Journal of Global Economics received 2175 citations as per Google Scholar report