Research Article - (2020) Volume 10, Issue 3
Received: 15-May-2020
Published:
15-Jun-2020
, DOI: 10.37421/jcde.2020.10.345
Citation: Ivanov, Vyacheslav N and Alisa A Shmeleva. “The Examples of Design of Normal Cycle Shells and Analyses of Stress-Strain State by Variation-Difference Method” Civil Environ Eng 10 (2020): 345 doi: 10.37421/jcde.2020.10.345
Copyright: © 2020 Ivanov VN, et al. This is an open-access article distributed
under the terms of the creative commons attribution license which permits
unrestricted use, distribution and reproduction in any medium, provided the
original author and source are credited.
The variation-difference method is a convenient numerical method for shells of complex forms. It is enough when only cinematic boundary conditions are satisfied because the method is based on the principle of Lagrange. Another advantage of the variation-difference method is the better opportunity to create computer programs based on it. For shell analysis in orthogonal coordinate system as well as for shell analysis in principal curvatures the system of equations describing stress-strain state can be simplified. In this paper the difference between analysis in orthogonal coordinate system and analysis in principal curvatures of the surface is considered. The main distinction of the analysis of shells in orthogonal curvilinear coordinate system is the necessity of determination of components which include curvature of torsion of coordinate lines. The addition of these components in the equations of the theory of shells for the coordinate system in principal curvatures gives possibility to analyze shells in common orthogonal coordinate system. In this article shell analysis in orthogonal coordinate system is applied to shells based on normal cyclic surfaces.
Normal cycle surfaces • Non-conjugated orthogonal coordinates • Thin-walled shells • Variation-difference method
One of the tasks of the modern town building is a design and working out the methods of analyses of space constructions of new complex forms [1]. There are the examples of using new complex forms of constructions in buildings in the 20-th 21-st centuries [2-5]. But the architects and mechanicengineers demand to develop and to investigate the new forms of the surfaces, which there are described by the analytical equation and their inculcation in different branches of science and technics. At the Encyclopaedia of analytical surfaces [6] there are described 35 classes of the surfaces. One of class of surfaces is the class of normal cycle surfaces, which allow constructing much new forms of thin shells [7-10]. Cycle shells formed by the system of circles are comfortable for their realization. At second half of the 20-th century there has been worked out the finite element method (FEM) for stress- strain analyses of constructions, which there are mainly used for design of thin shell. But in most program complexes of FEM there are not taken into account the geometrical characteristics of the middle surface of the shell, which may bring to not correct results of design of the shells of complex form. The alternative method of analyses of thin-walled shells of complex geometry is a variation-difference method. The program complex VRMSHELL which used the base of variationdifference method there is worked out at the chair of strength of materials of Engineering department RUDN (today, the Department Civil Engineering, Engineering Academy, RUDN) used the geometrical characteristics of the middle surface of the shell [11,12].
At the article there given the base of the geometry of the normal cycle surfaces and the variation-difference method, shone the examples of the normal cycle surfaces and the example of calculation of stress-strain state of the shell.
Geometry of normal cycle surfaces
Normal cycle surfaces there are formed by moving of a circle of change or constant radius at the normal plane of the directrix curve of centers of the generating circles. Vector equation of normal cycle surface:

where 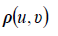 is a radius-vector of the surface;
is a radius-vector of the surface;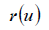 - radius-vector of
the directrix line of centers of the generating circles;
- radius-vector of
the directrix line of centers of the generating circles; 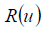 is a function of
radius of the generating circles;
is a function of
radius of the generating circles; 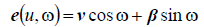 is the equation of
the circle of unit radius at the normal plane of the line of the centers of the
generating circles;
is the equation of
the circle of unit radius at the normal plane of the line of the centers of the
generating circles; 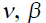 are vectors of normal and bi-normal of the line of the
circles;
are vectors of normal and bi-normal of the line of the
circles; 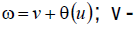 polar angle at the normal plane of the of the line of the
centers of the circles;
polar angle at the normal plane of the of the line of the
centers of the circles; 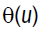 there is determining the initial polar angel from the
normal of the directrix line.
there is determining the initial polar angel from the
normal of the directrix line.
The block of the normal cycle shells allow to analyze any normal cycle shell with the plane directrix and the function of radius included at the library of curves of the program complex. If it is necessary to use some curve which is not at the library the new curve may be simply included at the library. There isn’t any another changes that must be done. For using of space direcrix it will be necessary to do some changes at the program complex.
Journal of Civil and Environmental Engineering received 1798 citations as per Google Scholar report