The Failure Mechanism of Reinforced Concrete Couple Shear Walls and Coupling Beams- A Ductility Approach

Sk Amjad Hossain^1* and Ashutosh Bagchi^2
*Correspondence: Sk Amjad Hossain, Department of Civil Engineering and Construction Management, The University of Texas, Tyler Houston Engineering Center, USA, Email:

Keywords

Coupled shear wall • Reinforced concrete • Failure mechanism • Ductility • Flexural displacement • Building code seismic • Force resisting systems.

Introduction

The coupled shear wall system is one of the effective potential Seismic Forces Resisting System (SFRS) in that have been using in midrise and high rise reinforced concrete buildings design. In seismic force resisting system it has to be ensure that the flexural displacement capacity which is known as ductility should be greater than the flexural displacement demand. The Canadian design standards, CSA A23.3 04 & 14, when confined reinforcements are required or not both are developed as per displacement-based approach and are expressed in terms of inelastic rotations. The inelastic displacement demands are calculated in ductility approach from displacement ductility demand and yield displacements, which is basically estimated from yield curvature, on the other hand inelastic displacement demand is an input in displacement approach. In displacement-based approach the low degree of coupled shear walls is modelled similar to the separate cantilever walls, on the other hand very high degree of coupled shear walls are modelled similar to the solid walls with openings. And, it is not properly justified to model coupled shear walls as solid cantilever shear walls with openings, since mass and stiffness distribution are not same for cantilever and coupled shear walls. Whereas, in terms of ductility perspective, one of the important phenomena that the curvature distribution in coupled shear walls at the points the system yields is completely different than cantilever shear walls. And that phenomenon is truly considered if rotational capacity and rotational demand are calculated in ductility approach in terms of reinforced concrete coupled shear walls design.

Objectives

The objectives of this study to investigate parameters that affect the load deflection behaviour of couple shear walls in ductility approach, using non-linear dynamic analysis. The analysis was performed using computer software SeismoStruct 2000. It was modelled a 12 storey building in Seismostruct 2000. Investigations were conducted on 14 different case studies with variation of different parameters like aspect ratio of the walls, depth span ratio of coupling beams, reinforcements of walls and coupling beams etc. And it will be investigating the influencing parameters that effect on the true load deflection behaviour calculating the displacement ductility demand and curvature ductility demand of the coupled shear walls and also effect of conventional reinforcement pattern on coupling beams.

Literature review: Ductility and plastic hinge length

In order to make proper seismic design of RC concrete wall, one of the important parts is to ensure flexural displacement capacity should be greater than flexural displacement demand. The inelastic portion of flexural displacement demand has been generated from a concentration of inelastic curvatures near the base of the wall. Usually, inelastic curvatures are assumed to be uniform over a height that is called plastic hinge length. Bohl A and Adebar P [1] performed a study to investigate the profile of inelastic curvatures that should be used to estimate the flexural displacement capacity of high-rise RC concrete walls. A handful numbers of study were performed earlier by different researchers summarized as follows. Not too many analysis and test results are available also in recent days in this field.

Especially for coupled shear wall, Adebar P, et al. [2] commented that, “To the author’s knowledge, there are no recommendations for plastic hinge length of coupled walls.” Chan WWL [3] proposed that the plastic hinge length is equal to the length over which reinforcement is yielding in any kind of wall. Sawyer HA [4] proposed a seminal equation for plastic hinge length in beams, where he assumed M_y/M_max =0.85 and determined l_p* = 0.15 z from Chan equation. He recognized that inelastic curvatures vary linearly from the maximum value to zero over this length and that the same inelastic rotation results from the maximum inelastic curvature being uniform over half of this length. He assumed that plasticity would spread over a length of d/4. Mattock AH [5] and Corley WG [6] performed tests on a large number of beams up to 750 mm deep and observed that plastic hinge length increases with effective depth d and shear span ratio (z/d) and decreases with the quantity of flexural tension reinforcements. Mattock AH [5] proposed modified plastic hinge length value in Sawyer HA equation.

Paulay T and Uzumeri SM [7] modified Sawyer’s equation by assuming that d = 0.8l_w and z = h_w to apply for concrete walls. Pauley T and Priestley MJN [8] recommended α =0.25 and β =0.044 in modified Sawyer’s equation for a lower bound estimate of plastic hinge length, l_p of concrete walls. Bohl A and Adebar P [1] proposed a simplified equation for maximum curvature at the base of the walls,

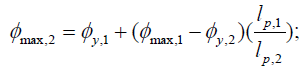
Where ϕ_max = maximum curvature at the base of the wall, ϕ_y = yield curvature and the subscripts 1 and 2 refer to the longer and shorter wall respectively.

In couple shear wall buildings, a system of couple shear wall is connected together by coupling beams. And, the systems of high degree of coupling are subjected to lateral loading, the shear force in the coupling beams induce high degree of axial force in the walls. One wall will be subjected to tension and other will be subjected to compression. Geometry of the coupling beam, span and the axial forces (tension and compression) are expected to have some effect on plastic hinge prediction.

The configuration of couple shear is consisting of by interconnecting beams connected along the height of the two coupled walls. The behavior of couple shear wall is mostly depend on the behavior of coupling beams and the failure of coupling beam is one of the failure modes of couple shear walls. The coupling beams should be designed as ductile inelastic manner for properly energy dissipations. The energy dissipations of the coupling beams depend on the yield moment capacity and the plastic rotation capacity of the coupling beams. If the yield moment capacity of the coupling beams is very high then it would undergo limited rotation and dissipate limited energy, on the other hand, if the yield moment capacity is not high, the couple beams may undergo much more than the plastic rotation capacity. Hence, the yield moment capacity should be optimized in order to properly design the coupling beams of the couple shear wall.

And, the yield moment capacity of the coupling beams also depends on the plastic rotation capacity.

Conventional reinforcement’s patterns are defined as the formation of longitudinal flexural reinforcements and transverse shear reinforcements. Longitudinal reinforcements consist of top and bottom reinforcement’s parallel to the longitudinal axis of the coupling beams and transverse reinforcements consists of formation of closely spaced ties along the length of the coupling beams.

Diagonal reinforcements in coupling beams consists of placement of reinforcements diagonally. It requires minimum four bars per diagonal for formation of the diagonal reinforcements. Though, it was not modelled the coupling beams under investigations with the diagonal reinforcements in this study. The diagonal reinforcements may be buckled if it is subjected to compressive loading in coupling beams. Under the reverse loading the reinforcement already buckled in one direction with compressive loading may be stressed in tension again. But this action could lead to low-cycle fatigue failure. To avoid this kind of circumstances, it is necessary to ensure that the reinforcements should not buckle. In the different building codes there is a minimum spacing required between two adjacent diagonal bars to prevent buckling due to the compressive loads.

Design provisions of coupling beams with different building codes:

US Code ACI-318 – 19/ ATC 40/ FEMA 273:

Conventional reinforcements (Tables 1-4)

Modeling in seismostruct

Geometric non-linearities are considered in seismostruct, modeling. Large displacement/ rotations and second order (nonlinear) effect that occurs when an axial load acts upon a lateral displacement generating an additional moment called (p-delta effect) are considered in the modeling through a total co-rotational formulation, which was developed by Correia AA and Virtuoso FBE [9]. Material non-linearity also considered in Seismostruct modeling. In seismostruct, fiber approach modeling is used to represent the cross-sectional behavior, where each fiber is modeled with uniaxial stress-strain relationship. Then, the sectional stress-strain state of beam column element is calculated through the integration of the non-linear uniaxial stress strain response of the individual fiber in which the section is subdivided, i.e., the discretization of the reinforced concrete section. In seismostruct modeling, it has been considered the distributed inelasticity instead of lumped inelasticity. In this research modelling recent developed Forced Based (FB) elements are considered for distributed inelastic finite element modeling. In terms of material inelasticity, it does have one advantage over Displacement Based (DB) elements model. With a displacement-based model refined discretization (meshing) are required, on the other hand, in Forced Based (FB) model it does not require. FB formulation does not depend on sectional constitutive behavior; hence the solution is always exact.

Methodology

A twelve-story building with a simple configuration with 14 different models (3 bays by 3 bays) are analyzed in SeismoStruct [10]. The seismic design parameters are considered for Vancouver location. It has been considered real seismic ground motions those are taken from PEER (Pacific Earthquake Research Institute). The selection of ground motion considers the ratio of peak Acceleration (A) to peak Velocity (V) close to 1, which represents the seismicity of Vancouver. The height of the building is considered 45.0 m. The design live load is equal to 2.4 kN/m² for all floors except the first storey which is 4.8 kN/ m². The snow load is calculated to be 2.3 kN/m². The dead load is 0.85 kPa exterior walls, 1.0 kPa for partition on floors, 0.5 kPa for ceiling and mechanical services for all floors and 0.5 kPa for roofing. The walls are considered ductile partially couple shear walls (NBCC-2015) with R_d=3.5 and R_o=1.6 for the lateral force resisting systems, where R_o and R_d are over strength and ductility factors respectively.

The building was modeled in SeismoStruct having a plan dimension 21 m × 21 m. The thickness of the couple shear wall is 650 mm. The wall thickness, the dimension of coupling beams is considered as per the minimum requirements of CSA A23.3-04 except the coupling beams are modelled with conventional reinforcement patterns.

In Seismostruct the concrete is modeled with Mander JB, et al. [11] non-linear concrete model and reinforcements are modeled with Menegotto Pinto steel model [10]. Dynamic time history analyses are performed with different wall length (L_w) 2 m, 2.5 m and 3 m and design parameters for that building.

In this study there are 06 coupling beams at different levels of the buildings are selected and investigated, those are CSH-223, CSH-255, CSH-2125, CSH- 423, CSH-455 and CSH-4125;

Chord shear force, bending moments, inelastic rotations and curvatures with different conditions for those coupling beams are summarized in Table 7 to 12; It has been summarized the geometric and material properties of 14 different models in Tables 5 and 6;

Analysis Results

Rotational capacity of coupling beam

The rotational capacity of coupling beams depends on various parameters. When the rotational demand is greater than the rotational capacity in a conventionally reinforced coupling beam, diagonally reinforcement could be provided as an alternative option and that depends also on Lb/db ratio of the coupling beam. In this research it has been conducted study with different Lb/ db ratio and conventional reinforcement and compares the rotational demand with rotational capacities with different building codes. Various research works were performed by different researchers, some of those are summarized in below Tables 1-4. (Tables 7-12)

Base shear vs. roof displacements in different models (12 storey buildings)

Non-linear dynamic analyses are performed and seismic base shear are calculated on 14 different models of the 12-storey building as described in methodology sections. Those base shear are plotted with respect to roof displacement, those are plotted in below Figures 1-27.

Calculation of ductility

The objectives of wall’s ductility provisions in earthquake resistant design are to ensure the curvature capacity ɸ_c should be greater than curvature demand ɸ_d imposed by any earthquake on it.

In ductility approach, total curvature demand is calculated from curvature ductility demand μ_ɸd and yield curvature ɸ_y.

The total displacement demand, which is calculated from an elastic portion referred as yield displacement Δ_y and an inelastic portion Δ_id. It can be estimated similarly from displacement ductility demand μ_Δd and yield displacements Δ_y.

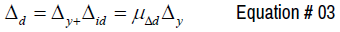
According to Paulay T and Uzumeri SM [7] the yield displacements at the top of the wall can be calculated from the yield curvature at the base of the wall assuming a first mode of curvature distribution.

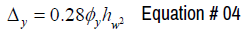
The total curvature demand ɸ_d is equal to summation of an elastic portion referred as yield curvature ɸ_y and inelastic curvature demand ɸ_id.

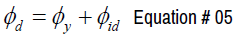
The inelastic curvature demand ɸ_id can be directly calculated from the inelastic displacement demand at the top of the wall Δ_id considering the displacement approach

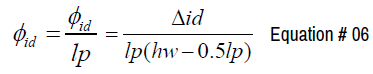
Combining equations 1-5 and rearranging to in order to solve curvature ductility demand the following equation can be found that is a function of displacement ductility demand μ_Δd

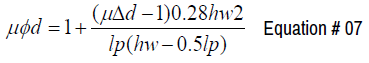
Calculation of displacement ductility demand (μ_Δd)

It has been considered the bi-linear relationship approach as shown in below Figures 28 and 29, Bhunia D, et al. [12] that was prepared based on the concept given in ATC 40; It is observed from the below Figure that the bilinear relationship approach is considered due to the initial tangent stiffness and equal energies concept, i.e., Area a₁ equal to Area a₂;

Hence, the ductility of the coupled shear can be calculated:

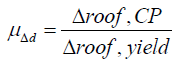
μ_Δd has been calculated from 14 different model and populated in Table 13. It has been considered fixed base boundary condition for modelling of all 14 different cantilever coupled shear walls.

Curvature ductility demands μ_ɸd are calculated with 14 different models considering different equations for plastic hinge length (l_p) with respect to ACI- 318, 19, CSA A23.3-04, CSA A23.3- 14 and authors formula and populated in Table 14.

Total curvature demands are calculated using the equation # 2,

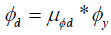
It has been populated in Table 15.

Calculation of curvature capacity

In a ductile shear wall (R/γ=4) the maximum compression zone length, c is permitted as per CSA A23.3-14 is equal to 0.14L_w, where L_w is length of the shear wall. It has been calculated the curvature capacity considering this maximum compression zone length criteria and populated in Tables 16 and 17.

In Table 16, it is considered plastic hinge length equation as per CSA A23.3-04 and in Table 17, it is considered the plastic hinge length equation as per CSA A23.3-14.

It is checked also at yielding consideration by considering c = 0.25*L_w, since c = 0.14* Lw is the maximum limit for ductile shear wall as per CSA A23.3-14, c =0.25*L_w is the reasonable assumption when the first reinforcement will be yielding. This curvature capacity are populated in Table 18. Basically, this is representing the yield curvature.

Research Findings

(1) Conventional reinforcements in coupling beams: In this research all the coupling beams are modelled with conventional reinforcements instead of diagonal reinforcements as recommended in CSA A23.4 04. It is observed on the selected coupling beams in this research that rotational demands are within the limit of the rotational capacities.

(2) It is observed by comparing curvature demands, those are shown in Table 15 with the curvature capacities, those are populated in Tables 16 to 21. The followings observations are made. In a ductile (R/r_w = 4). shear wall the compression zone length maximum limit assumption (c = 0.14*L_w) as per Canadian code CSA A23.3 04 is not working in coupled shear wall in both of the cases where plastic hinge length (L_p) is considered individual length of the compression or tension wall as per (CSA A23.3 04) [13] and also where the plastic hinge length is considered overall length of the couple shear wall as per (CSA A23.3 14) [14];

(3) Coupled shear wall design approach: Considering ductility approach calculations in coupled shear wall design, it can be commented that separate formula needs to be developed to calculate rotational demand vs rotational capacity and curvature demand vs curvature capacity and also the plastic hinge length for cantilever shear wall and coupled shear wall both.

(4) It is observed from Table 19 that the maximum compression zone length (c = 0.11* L_w) formula working as per CSA A23.3 04, where the plastic hinge length (L_p) calculation allows to consider individual length of the walls but it does not work as per CSA A23.3 14, where the calculation of plastic hinge length allows to consider overall length of the coupled shear wall.

(5) It is observed the curvature capacities from Tables 20 and 21 and comparing with the curvature demand Table 15, the maximum compression zone length (c = 0.09*L_w) works for all three codes CSA A23.3 04, CSA A23.3 14 and ACI-318 19, where it has been considered the plastic hinge length (L_p) calculations as per the corresponding building codes.

Conclusion

It can be commented that it is not properly justified to model and treat the coupled shear wall as a solid cantilever wall with opening since mass and stiffness distribution are not same for cantilever and coupled shear walls. In order to get accurate prediction of failure mechanism of coupled shear wall and coupling beams, it is very important to model and analyze it as a ductility approach. In this research it was investigated with non-linear dynamic analysis of 14 different models of a twelve-story coupled shear wall buildings as per CSA A23.3 14 except the coupling beams are modeled with conventional reinforcements. Study shows that the maximum flexural compression zone length without confinement reinforcement as per (CSA A23.3 1994) is not working with slender coupled shear walls (tension or compression wall), while considering the plastic hinge length as per CSA-A23.3 04 or CSA-A23.3 14; Separate formula is proposed for the maximum compression zone length limitation by analyzing the coupled shear wall in ductility approach and investigation shows that the proposed formula represents the accurate behavior of the coupled shear wall maximum compression zone length limitation that works while the plastic hinge length calculations done by CSA A23.3 04, CSA A23.3 14 and ACI 318 19. Since, wall overstrength (γ_w) has little influence on the maximum flexural compression zone length of the coupled shear wall, it has not been investigated its influence on this research.

As this research is based on seismicity of Vancouver and National Building Code of Canada on the coupled shear wall, similar work can be performed considering different seismicity and other National Building codes.

Acknowledgement

None.

Conflict of Interest

The authors declare that there is no conflict of interest.

References

1. Bohl, Alfredo and Perry Adebar. "Plastic hinge lengths in high-rise concrete shear walls." ACI Struct J Am Concr 109 (2012): 123.

Google Scholar, Crossref, Indexed at

2. Adebar, Perry, James Mutrie and Ronald DeVall. "Ductility of concrete walls: The Canadian seismic design provisions 1984 to 2004." Can J Civ Eng 32 (2005): 1124-1137.

Google Scholar, Crossref, Indexed at

3. Chan, W. W. L. "The ultimate strength and deformation of plastic hinges in reinforced concrete frameworks." Mag Concr Res 7 (1955): 121-132.

Google Scholar, Crossref, Indexed at

4. Sawyer, Herbert A. "Design of concrete frames for two failure stages." Spec Publ 12 (1965): 405-437.

Google Scholar, Indexed at

5. Mattock, Alan H. "Rotational capacity of hinging regions in reinforced concrete beams." Spec Publ 12 (1965): 143-181.

Google Scholar 

6. Corley, W. Gene. "Rotational capacity of reinforced concrete beams." J Struct Eng 92 (1966): 121-146.

Google Scholar

7. Paulay, T. and S. M. Uzumeri. "A critical review of the seismic design provisions for ductile shear walls of the Canadian code and commentary." Can J Civ Eng 2(1975): 592-601.

Google Scholar, Crossref, Indexed at

8. Paulay, Thomas and M. J. N. Priestley. "Stability of ductile structural walls." J Struct 904 (1993): 385-392.

Google Scholar, Indexed at

9. Correia, António A. and Francisco BE Virtuoso. "Nonlinear analysis of space frames." III European Conference on Computational Mechanics: Solids, Structures and Coupled Problems in Engineering: Book of Abstracts, Springer Netherlands (2006): 107-107.

Google Scholar, Crossref, Indexed at

10. https://seismosoft.com/support/seismostruct-support/
11. Mander, John B., Michael JN Priestley and Robert Park. "Theoretical stress-strain model for confined concrete." J Struct Eng 114 (1988): 1804-1826.

Google Scholar, Crossref, Indexed at

12. Bhunia, Dipendu, Vipul Prakash and Ashok D. Pandey. "Research article a conceptual design approach of coupled shear walls." (2013).

Google Scholar, Crossref, Indexed at

13. https://www.csagroup.org/store/product/2417424/
14. https://www.csagroup.org/store/product/A23.3-14/