Research Article - (2020) Volume 14, Issue 2
Received: 05-May-2020
Published:
23-Jul-2020
, DOI: 10.37421/1736-4337.2020.14.301
Citation: Dalal, Soham Mohan. “The Intersect Point Theorem.” J Generalized Lie Theory Appl 14 (2020): 301. doi: 10.37421/GLTA.2020.14.301
Copyright: © 2020 Dalal SM. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In this paper titled 'The Intersect Point Theorem,' I had performed many mathematical operations on a figure formed by three non-collinear points called a triangle. In this paper
a concept, when two lines intersect at a common point on one of the segments of the triangle, then their cause is defined. I had tried to keep my work in the ordinary language
of Geometry. All these principles keep me on researching various geometrical concepts throughout the year.
Non-collinear points • Geometry • Operations
C.S.C.T: Corresponding Side of Congruent Triangles • C.A.S.T: Corresponding Angles of Similar Triangles
The theorem is based on basic geometrical concepts. I had performed many mathematical operations on a triangle which would further introduce the world new theorem which is proved logically in mathematical sciences.
In a triangle, when two lines intersect at a point and touch the one segment of the triangle, then that segment is twice the length of one of the intersecting lines.
Theorem
In a triangle, when two lines intersect at a point and touch the one segment of the triangle, then that segment is twice the length of one of the intersecting lines.
Construction
Draw segment AP BC (i.e B-P-C).
I assumed in Figure 1, triangle ABC, angle ABC=angle ACB.
Figure 1. 
ABC.
Segment QR // segment BC, segment QP // segment Ac (by mid-point statement) [1-3]
And segment QR is a bisector of angle AQP (i.e angle AQP=angle PQO).
Likewise, segment QP is a bisector of angle BPA (i.e angle QPB=angle QPO).
To prove: segment AB=½ QP.
Proof: If segment PO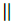 
QR and segment AO 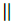QR then, Angle AOQ ≅ angle POQ=90 [4] (1)
Angle AQO ≅ angle PQO ------------- (given) (2)
Now in triangle AQO and triangle PQO, Angle AOQ ≅ Angle POQ (from 1)
Angle AQO ≅ Angle PQO (from 2)
Triangle AQO~Triangle PQO (AA Test) [5]
Angle QAO ≅ Angle QPO------- (c.a.s.t) (3)
Now in triangle AQO and triangle PQO, Angle QAO ≅ Angle QPO (from 3)
Angle QAO ≅ Angle QOP (each 90° )
Segment QO ≅ Segment OQ (common side)
Triangle AQO ≅ Triangle PQO (AAS Test) [6]
Segment AQ ≅ Segment QP ---------- (c.s.c.t) (4)
Now angle ABC ≅ angle ACB ----- (Given) (5)
Segment QP // segment AC and BC is a transversal, Angle QPB ≅ Angle BCR (corresponding angles) [7]
i.e angle QPB=angle ACB (6)
i.e Angle QPB=Angle ABC (from 5)
Segment QP ≅ Segment BQ ---- (converse of isosceles triangle theorem) [8] (7)
Now,
Segment AQ ≅ Segment QP (from 4)
And segment BQ ≅ segment QP (from 7)
Now, if AQ+BQ=AB
QP+QP=AB (from 8)
2QP=AB
i.e QP=1/2 AB
∴ HENCE PROVED
Firstly-in a triangle, when two lines intersect at a point and touch the one segment of the triangle, then that segment is twice the length of one of the intersecting lines. This Statement is proved above by giving the notions of Euclidean Geometry. Secondly, we may find the length of QP=½ AB by certain Measurements mentioned in Figure 1.
By these theorems, the world may introduce to the new way of finding the length of the side of a triangle, the segment joining the two mid-points of a triangle and we might get a complete solution by proving the theorem mentioned in methodology.
