The Iterative Solution of Taylor Formula for Partial Differential Equation

Yang Gao^*
*Correspondence: Yang Gao, Department of Science, Binzhou University, Binzhou, China, Email:

Keywords

Taylor's formula • Iteration method • Nonlinear • Partial differential equation

Introduction

This paper introduces that Taylor formula iteration method resolve partial differential equation. In this paper, six examples are used to introduce Taylor formula iteration method to solve partial differential equation. This paper also introduce that Generalized Taylor's formula can solve fractional partial differential equation. The iterative method of Taylor formula is an important and useful method to solve partial differential equation [1-10]. The solution of Taylor formula iteration method belongs to C^∞.

Variable coefficient problem

We consider equation as following:

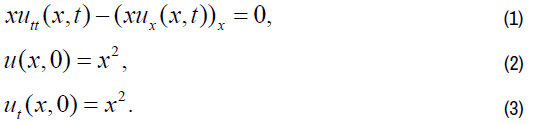
We solve (1) by Taylor formula iteration method as following:

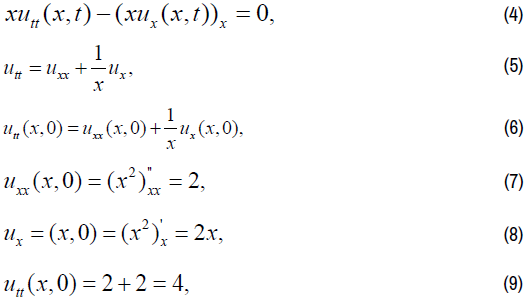
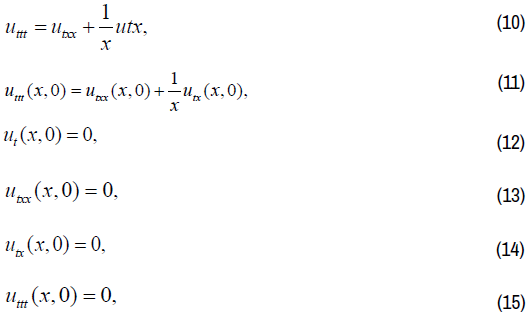
And we have:

By Taylor's formula, we get as following:

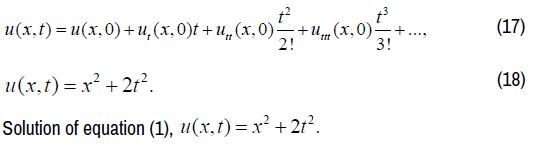
Two dimensional heat conduction equation solution

We study the equation as following:

Next, we solve (19) by Taylor formula iteration method,

On equation (21), finding 1-order partial derivative of t on both sides,

We have:

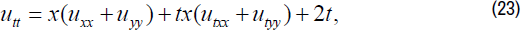
On equation (23), finding 1-order partial derivative of t on both sides,

We have:

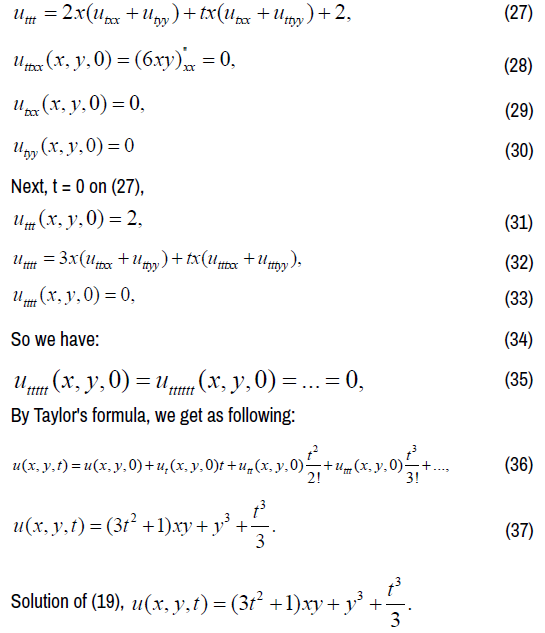
The third problem with boundary values

We consider following equation:

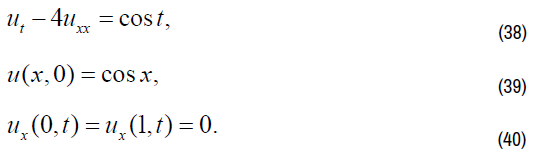
By Taylor formula iteration method, we have:

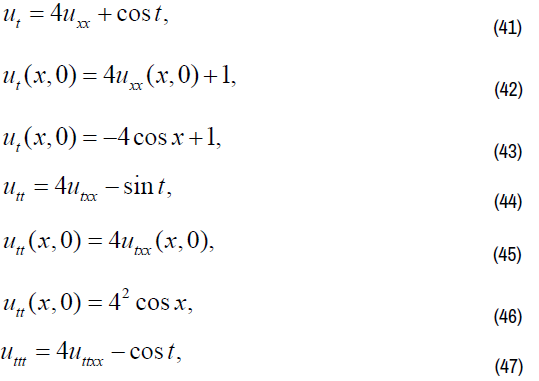
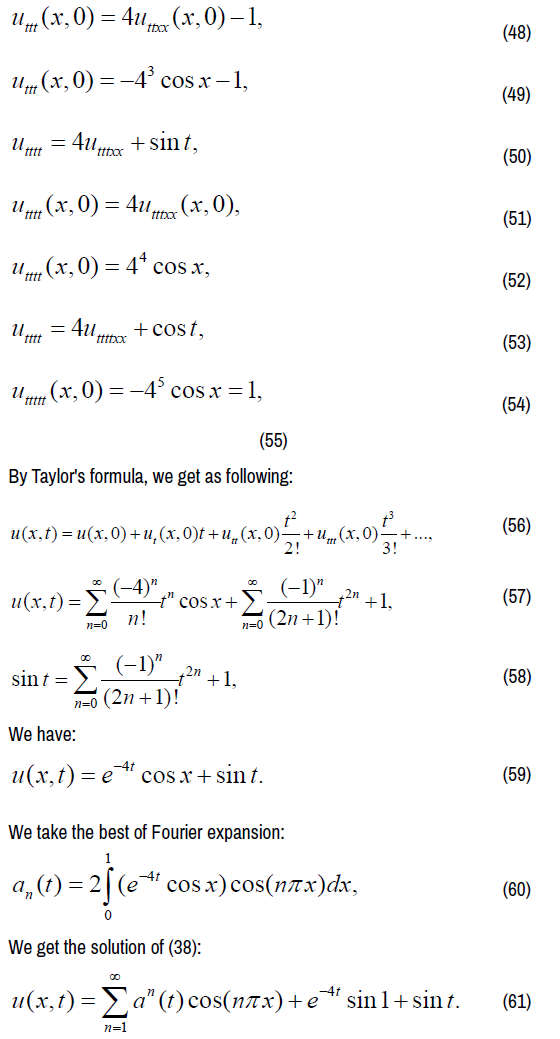
Fractional partial differential equation

We consider following fractional partial differential equation:

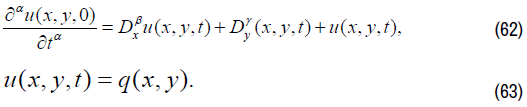
Where q(x,y)is known integral polynomial.

The definition of Caputo fractional derivative about t:

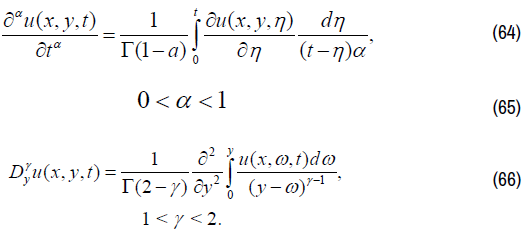
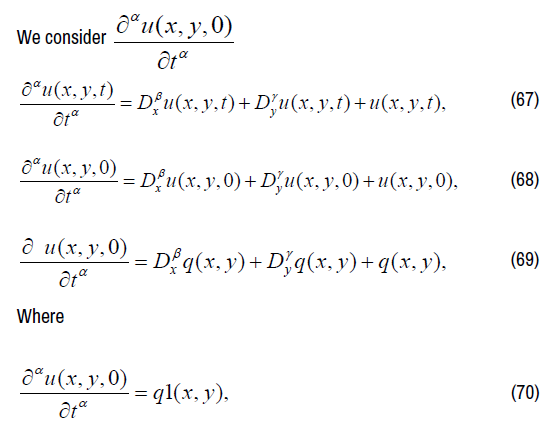
q1(x,y) is known function.

We consider 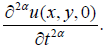On equation (62), finding α -order partial derivative of t on both sides,

We have:

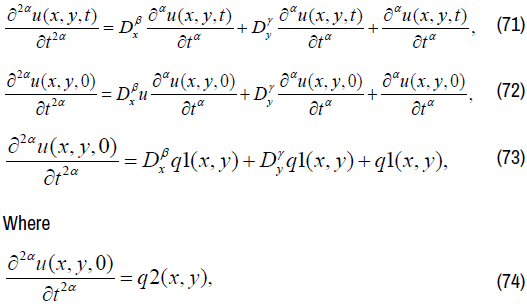
q2(x,y) is known function.

We consider 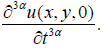on equation (62), finding 2α -order partial derivative of t on both sides,

We have:

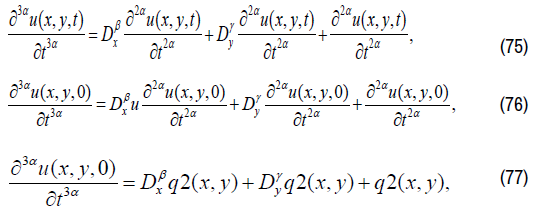
Where

q3(x,y) is known function. We consider 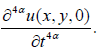on equation (62), finding 3α -order partial derivative of t on both sides,

We have:

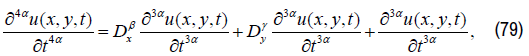
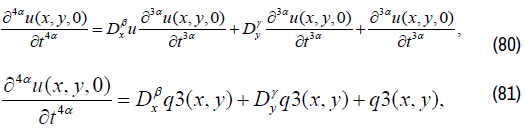
Where

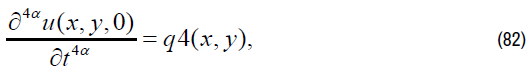
q4(x, y) is known function. We have:

q_n(x, y) is known function.

By Generalized Taylor's formula:

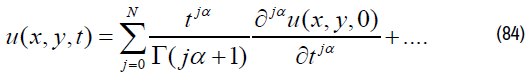
So we have the solution of (62):

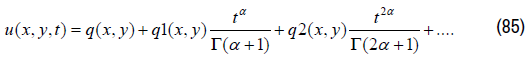
Nonlinear KdV equation

We consider the wave equation as following:

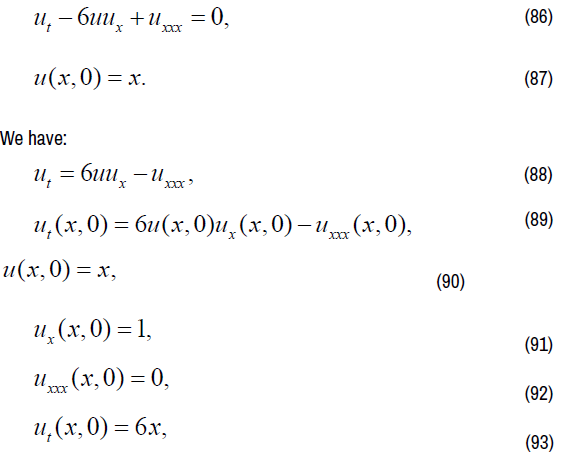
On equation (88), finding 1-order partial derivative of t on both sides,

We have:

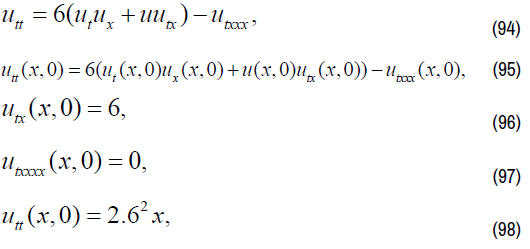
On equation (94), finding 1-order partial derivative of t on both sides,

We have:

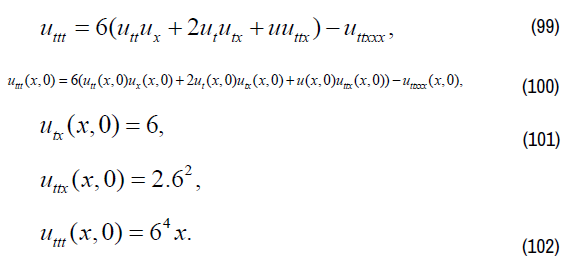
By Taylor's formula, we get as following:

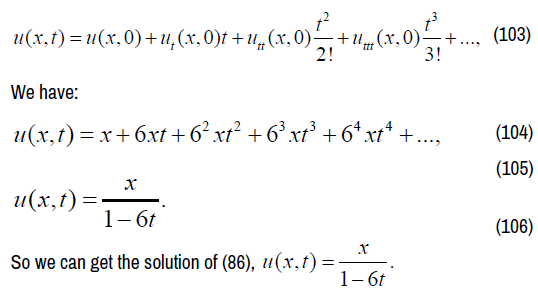
Nonlinear sine-Gordon equation

We consider following constant coefficient equation

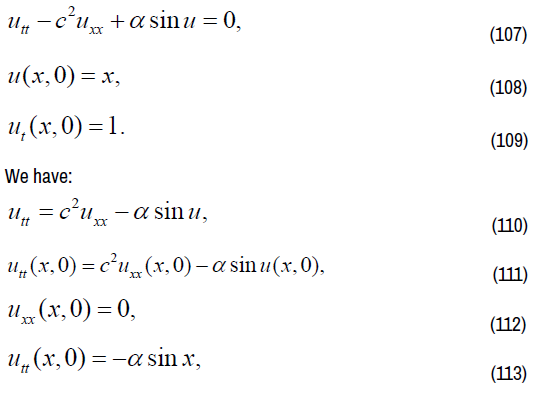
On equation (110), finding 1-order partial derivative of t on both sides,

We have:

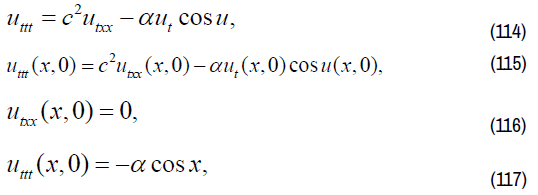
On equation (114), finding 1-order partial derivative of t on both sides,

We have:

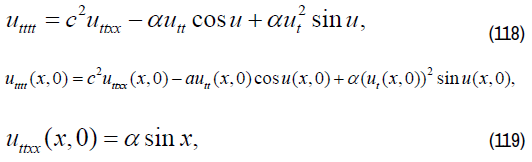
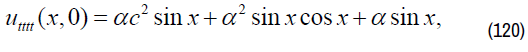
u_ttttt(x,0),u_tttttt(x,0)…is known function.

By Taylor's formula, we get as following:

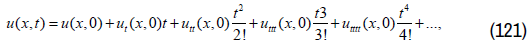
So we can get the solution of (107).

Conclusion

Iterative solution of partial differential equations by Taylor formula is important and good methods that solve linear and nonlinear partial differential equations. And the method also can solve fractional partial differential equations.

References

1. Bahri, Abbas and Haïm Brézis. "Periodic solutions of a nonlinear wave equation." Proc R Soc Edinb A 85 (1980): 313-320.

Google Scholar, Crossref

2. Bamberger, Alain, Guy Chavent and Patrick Lailly. "About the stability of the inverse problem in 1-D wave equations—Application to the interpretation of seismic profiles." Appl Math Optim 5 (1979): 1-47.

Google Scholar, Crossref, Indexed at

3. Barbu, V and N. H. Pavel. "Periodic solutions to one-dimensional wave equation with piece-wise constant coefficients." Differ Equ 132 (1996): 319-337.

Google Scholar, Crossref, Indexed at

4. Barbu, V and N. H. Pavel. "Determining the acoustic impedance in the 1-D wave equation via an optimal control problem." SIAM J Control Optim 35 (1997): 1544-1556.

Google Scholar, Crossref, Indexed at

5. Barbu, V and N. H. Pavel. "Periodic solutions to nonlinear one dimensional wave equation with x-dependent coefficients." Trans Am Math Soc 349 (1997): 2035-2048.

Google Scholar, Indexed at

6. Brézis, Haïm. "Periodic solutions of nonlinear vibrating strings and duality principles." Bull New Ser Am Math Soc 8 (1983): 409-426.

Google Scholar, Crossref, Indexed at

7. Brezis, H and L. Nirenberg. "Forced vibrations for a nonlinear wave equation." Commun Pure Appl Math 31 (1978): 1-30.

Google Scholar, Crossref, Indexed at

8. Craig, Walter and C. Eugene Wayne. "Newton's method and periodic solutions of nonlinear wave equations." Commun Pure Appl Math 46 (1993): 1409-1498.

Google Scholar, Crossref, Indexed at

9. Ding, Yanheng, Shujie Li, and Michel Willem. "Periodic solutions of symmetric wave equations." Differ Equ 145 (1998): 217-241.

Google Scholar, Crossref, Indexed at

10. Gao Yang, HeYuan.Wang, "Taylor's formula and partial differential equation." (2015):1008-1399.