Research - (2020) Volume 11, Issue 1
Received: 21-Jan-2020
Published:
13-Feb-2020
, DOI: 10.37421/2155-6180.2020.11.436
Citation: Zitouni Mouna. The Kumaraswamy-Rani Distribution and Its Applications. J Biom Biostat 11 (2020) doi: 10.37421/jbmbs.2020.11.436
Copyright: © 2020 Mouna Z. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In this paper, a new distribution called the Kumaraswamy-Rani (KR) distribution, as a Special model from the class of Kumaraswamy Generalized (KW-G) distributions, is introduced. Its statistical properties are explored. Estimation parameters based on maximum likelihood are obtained. We have illustrated the performances of the proposed distribution by some simulation studies. Finally, the significance of the KR distribution in terms of modeling real data set has been highlighted before it has been compared to some one parameter lifetime distributions.
Fixed point method • Kumaraswamy distribution • Maximum likelihood estimation • Newton-raphson method • Rani distribution
Modeling and analysis of lifetime data is an important aspect of statistical work in such wide variety of scientific and technological fields as medicine, engineering, insurance and finance...
Therefore, the construction of the distributions is the most important work from a probabilistic point of view and recently many researchers are concentrated in this area [1-3].
More that, varying lifetime distributions and their generalizations have been created as exponential, Lindley, gamma, lognormal, Weibull, Sujatha, Akash, Rani. Further, A two-parameter family of distributions on called Kumaraswamy distribution is explored. It was introduced by Kumaraswamy [4]. It has the flexibility in modeling lifetime data.
The latter exhibits many similarities to the beta distribution and a number of advantages in terms of tractability which has been discussed by Jones [5]. Among these advantages, we mention: a simple explicit formula for its distribution function, its quantile function. L-moments and moments of order statistics [6]. In this direction, another new one parameter lifetime distribution has attracted the attention of statisticians and whetted then interest named Rani distribution. It was proposed by Rama Shanker and it has important statistical properties [7]. For the motivating properties of the Kumaraswamy and Rani distributions, we shall introduce a new probability distribution based on the Kumaraswamy distribution and the Rani distribution. The proposed distribution is called the Kumaraswamy-Rani (KR) distribution with twos positive parameters denoted b and β. In this study some statistical properties of this distribution are derived to show their applicability in the real lifetime data analysis. The rest of the paper is organized as follows. In Section 2, the KR distribution is identified in addition, some important mathematical properties of the new distribution are presented. In Section 3, maximum likelihood estimation is discussed. In section 4, some simulation studies are reported. A real lifetime data set are used in Section 5 to illustrate the usefulness of the KR distribution. Finally, our work is crowned with conclusion.
The Kumaraswamy-Generalized distribution
The cumulative density function (cdf) of the Kumaraswamy-Generalized (Kum-Generalized) distribution proposed by Cordeiro et al. [8] is given by
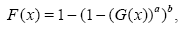 (1)
(1)
Where a>0, b>0 are shape parameters and G is the cdf of a continuous random variable X. Consquently, the Kumaraswamy-Generalized distribution has the probability density function (pdf) specified by
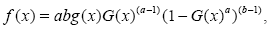 (2)
(2)
where, 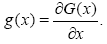
According to Cordeiro et al. [8], using the binomial expansion for  , equation (2) can be rewritten as
, equation (2) can be rewritten as
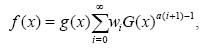 (3)
(3)
where the binomial coefficient wi is defined for all real numbers with,
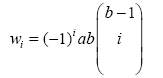
The Rani distribution
The Rani distribution is proposed by Rama Shanker [7]. It is defined over the support x>0 and it has the pdf given by:
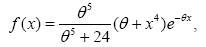 (4)
(4)
where θ is the scale parameter of the Rani distribution denoted R(θ). The latter is a mixture of exponential (θ) and gamma (5,θ) with mixing proportion 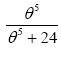 . Furthermore, the corresponding cumulative distribution function (cdf) is given by:
. Furthermore, the corresponding cumulative distribution function (cdf) is given by:
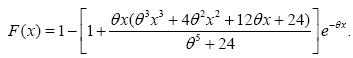 (5)
(5)
The KR distribution
In this subsection, we give the new distribution called KR distribution. It is formulated using the Rani (θ>0) and the Kumaraswamy (a = 1,b > 0) distributions.
The KR density for x>0 is expressed as
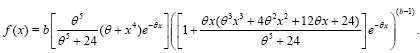 (6)
(6)
The parameters vector of the KR distribution is 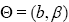 . Moreover, using equation (3), equation (6) can be defined as:
. Moreover, using equation (3), equation (6) can be defined as:
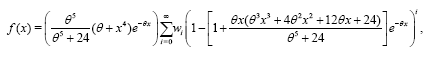 (7)
(7)
where 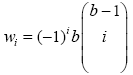
Remark 1: Let  . If b=1, then
. If b=1, then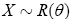 (Figure 1).
(Figure 1).
We can find easily the cumulative distribtion function (c.d.f) of the KR distribution
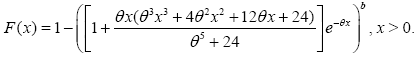 (8)
(8)
Using the c.d.f in order to obtain the Survival function (Figure 2):
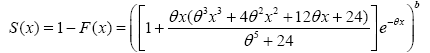
and the Hazard function which is an important quantity characterizing life phenomena is given by
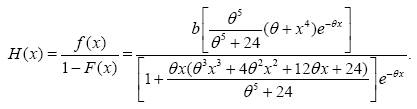
Now, we shall introduce the following Theorem about the inverse cumulative KR distribution. The latter characterizes the proposed distribution.
Theorem 2.1: Let 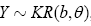 then
then 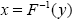 is the zero of the polynomial equation given by
is the zero of the polynomial equation given by
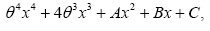 (9)
(9)
where,
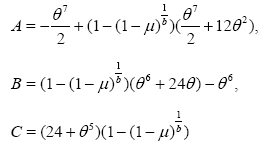
and 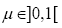 .
.
Proof: In order to get the zero of equation (9), we shall introduce the following equation:
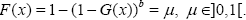
So,
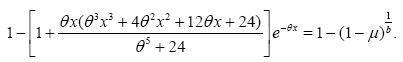
We have also,
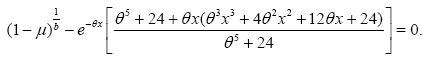
In the following, we get,
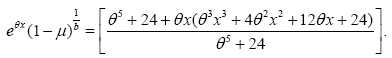
It is to be noted that the limited development to order 2 of exponential function at 0 can be written as:
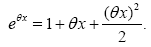
Then, we obtain:
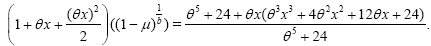 (10)
(10)
Applying some mathematical treatments on equation (10) yields,
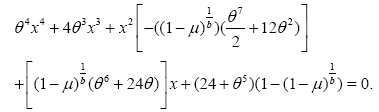
Proving that
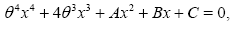
where,
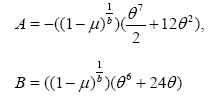
and
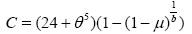
which completes this proof.
In this section, the maximum likelihood method for the parameters estimation of the KR distribution is derived. For this reason, a brief description of the method for the fitting of the KR parameters is presented. The likelihood function for the parameters is given by
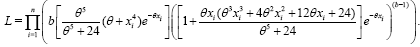 (11)
(11)
The log-likelihood is formulated as:
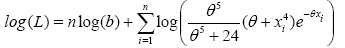
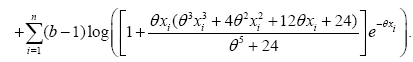 (12)
(12)
In order to get the maximum likelihood estimators of (b,θ), the first order partial derivatives function of log(L) is calculated, with respect to the KR parameters which are given respectively by:
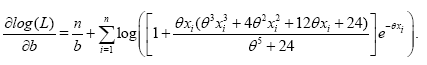 (13)
(13)
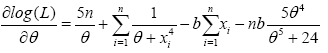
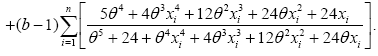 (14)
(14)
By setting these above equations to zero, we get
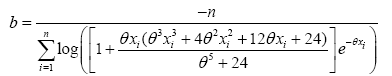 (15)
(15)
and
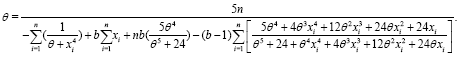
Hence, the maximum likelihood estimators of b and θ can be obtained by using the fixed point method or Newton - Raphson method or other numerical methods.
Let us consider some simulation studies to illustrate the usefulness of the new distribution. By applying the inverse transformation technique, we simulated two random samples having size 5000 from KR distribution, with the parameter vectors (b=2, θ=3) and (b=5, θ=2) respectively (Figures 3 and 4).
From the above Histograms and compared to the curve of the proposed density, it is worth noting that we have generated samples from a KR distribution.
Our basic objective in this section is to motivate the use of the KR distribution by showing a successful application to modeling lifetime data set given [9] which represents the relief times of twenty patients receiving an analgesic. The data are as follows: 1.1,1.4,1.3,1.7,1.9,1.8,1.6,2.2,1.7,2. 7,4.1,1.8,1.5,1.2,1.4,3.0,1.7,2.3,1.3,2.0
We use the lifetime data set given above to evaluate the effectiveness of the new distribution with three distributions: Rani, Akash and Sujatha distributions [7,10,11]. To assess the goodness-of-fit of above models, we used the Akaike information criterion (AIC), the Akaike Information Criterion Corrected (AICC), the Bayesian information criterion (BIC) and the Loglikelihood L, which are calculated according to the following formula:
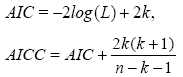
and
BIC = −2log(L) + klog(n)
where, n is the number of observations in the sample and k represents the number of parameters.
The maximum likelihood estimates of the parameters 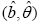 , the Akaike Information Criterion (AIC) the Akaike Information Criterion Corrected (AICC), the Bayesian Information Criterion (BIC) and the log-likelihood L values for the corresponding distributions are reported in Table 1.
, the Akaike Information Criterion (AIC) the Akaike Information Criterion Corrected (AICC), the Bayesian Information Criterion (BIC) and the log-likelihood L values for the corresponding distributions are reported in Table 1.
| Distributions | Maximum Likelihood estimates | AIC | AICC | BIC | L |
|---|---|---|---|---|---|
| KR | 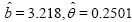 |
58.2524 | 58.9582 | 60.2439 | -27.1262 |
| Rani | 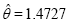 |
65.4474 | 65.6697 | 66.4432 | -31.7237 |
| Akash | 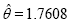 |
67.4118 | 67.6340 | 68.4075 | -32.7059 |
| Sujatha | 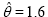 |
66.8815 | 66.8824 | 73.2935 | -32.4407 |
According to the small values of both AIC, BIC and AICC the proposed distribution performs better than the other candidate models. In addition, referring to the big L values for the KR distribution, we infer that the latter provides a good fit for the given data and it proves therefore to be the more appropriate model.
In this paper, we set forurerd a new distribution namely the KR distribution. It is formulated using the Kumerswamy-generalized distribution and the Rani distribution. We provide a mathematical treatment of the new distribution including cumulative, Hazar and Survival functions. We discuss a maximum likelihood estimation of the model’s parameters. An application of the new distribution to a real data set is presented to demonstrate that it can be used quite effectively to provide better fits than other available models. We aspire this generalization may attract wider applications in survival analysis.
Journal of Biometrics & Biostatistics received 3496 citations as per Google Scholar report