The Osmotic Dehydration of Shark Fillets Modelled Mathematically

Sik Yang^*
*Correspondence: Sik Yang, Department of Mathematical Sciences, Beijing University of Technology, Beijing, China, Email:

Description

Modelling the osmotic dehydration of shark fillets mathematically involves understanding the mass transfer processes that occur during the dehydration process. Osmotic dehydration is a method used to remove water from food products by immersing them in a hypertonic solution, causing water to move out of the food matrix. This process is influenced by various factors including temperature, concentration of the osmotic solution, size and shape of the food particles, and duration of the process, A simplified mathematical model for osmotic dehydration of shark fillets can be based on Fick's second law of diffusion, which describes the diffusion of water in a solid material, The general form of Fick's second law for one-dimensional diffusion is

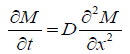
Where

• M is the moisture content of the shark fillets.
• t is time
• x is the spatial coordinate (thickness of the shark fillets).
• D is the effective diffusion coefficient.

This equation represents the rate of change of moisture content with respect to time, which is proportional to the second derivative of moisture content with respect to the spatial coordinate.

To incorporate the effect of osmotic solution, we can use a mass balance equation, considering the transfer of water from the shark fillets to the surrounding solution:

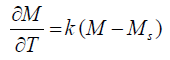
Where:

• M_s is the equilibrium moisture content of the shark fillets in the osmotic solution.
• k is the mass transfer coefficient.

Combining these equations, we get:

This equation represents the diffusion of water within the shark fillets and the mass transfer between the shark fillets and the osmotic solution. The boundary and initial conditions need to be specified based on the experimental setup. Solving this partial differential equation numerically or analytically will provide the moisture content profile of the shark fillets over time during osmotic dehydration. This model can be further refined by considering additional factors such as temperature dependence, concentration gradients, and other process parameters. Experimental validation and parameter estimation are essential steps to validate the model's accuracy and applicability. The rate of mass transfer and diffusion coefficients can be temperature-dependent. This can be incorporated by modifying the diffusion coefficient D and the mass transfer co-efficient k as functions of temperature. The concentration gradient between the shark fillets and the osmotic solution plays a significant role in driving the mass transfer. This can be accounted for by considering the concentration profiles within the shark fillets and the osmotic solution. Geometry of the shark fillets affects the diffusion path length and surface area available for mass transfer. Models can be adapted to account for different shapes and sizes of the fillets, in some cases, the osmotic dehydration process may exhibit nonlinear behaviour, particularly at high concentrations or extended durations. Non-linear models or empirical correlations may be necessary to capture such effects [1-5].

Mathematical modelling of the osmotic dehydration process for shark fillets offers a powerful tool for understanding and optimizing this preservation technique. By incorporating factors such as temperature dependence, concentration gradients, size and shape effects, non-linear behaviour, solute interactions, and mass transfer limitations, the model can provide insights into the complex dynamics of water removal from the fillets. Through numerical or analytical solutions of the governing equations and validation against experimental data, the model can be refined to accurately predict moisture content profiles and optimize process parameters. This facilitates efficient use of resources, minimizes processing time, and ensures the quality and safety of the dehydrated shark fillets. Furthermore, sensitivity analysis can identify critical parameters, guiding experimental efforts and focusing attention on areas where improvements are most needed. Ultimately, a well-developed mathematical model enhances our understanding of osmotic dehydration processes, supporting the development of effective preservation strategies for shark fillets and other food products.

Acknowledgement

None.

Conflict of Interest

None.

References

1. Ashcraft, Mark H and Elizabeth P. Kirk. "The relationships among working memory, math anxiety, and performance." J Exp Psychol 130 (2001): 224.

   Google Scholar, Crossref, Indexed at

2. Hopko, Derek R, Rajan Mahadevan, Robert L. Bare and Melissa K. Hunt. "The Abbreviated Math Anxiety Scale (AMAS) construction, validity, and reliability." Assessment 10 (2003): 178-182.

   Google Scholar, Crossref, Indexed at

3. Hadwin, Julie A and Helen J. Richards. "Working memory training and CBT reduces anxiety symptoms and attentional biases to threat: A preliminary study."Front Psychol 7 (2016): 47.

   Google Scholar, Crossref, Indexed at

4. Baron, Reuben M and David A. Kenny. "The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations."J Pers Soc Psychol 51 (1986): 1173.

   Google Scholar, Crossref, Indexed at

5. Artemenko, Christina, Gabriella Daroczy and Hans-Christoph Nuerk. "Neural correlates of math anxiety–an overview and implications." Front Psychol 6 (2015): 1333.

   Google Scholar, Crossref, Indexed at