Research Article - (2024) Volume 15, Issue 3
Received: 23-Jan-2023, Manuscript No. JBSBE-22-87542;
Editor assigned: 26-Jan-2023, Pre QC No. JBSBE-22-87542 (PQ);
Reviewed: 10-Feb-2023, QC No. JBSBE-22-87542;
Revised: 23-Mar-2023, Manuscript No. JBSBE-22-87542;
Published:
31-Mar-2023
, DOI: 10.37421/2155-6210.2023.13.354
Citation: Jacobs, Fritz C. "The Unification of Coulomb�¢??s
Electrostatic Law with Newton�¢??s Gravitational Law: A Generalized Model." J
Biosens Bioelectron 14 (2023):355.
Copyright: �?�© 2023 Jacobs FC. This is an open-access article distributed under the terms of the creative commons attribution license which permits unrestricted use,
distribution and reproduction in any medium, provided the original author and source are credited.
Our search for the unification of electrostatic force and gravity is one of the most pressing research areas. Sir Newton’s universal gravitational constant G is and has been the key constant in the calculations of classical mechanics for the gravitational potential and force of attraction between two masses, as well as the motion in the solar system. Recent research work on gravity focused on finding low-frequency gravitational waves. In this paper it is shown that, Newton’s gravitational law and Coulomb’s electrostatic law are manifestations of the same fundamental interactions. G depends on the quantum physical composition of matter, being the atomic number/protons (Z) to atomic mass number (A) ratio. All planets orbiting the sun yield, within statistical significance, the same G. However, the reference frame of atomic nuclei is distinctly different for each element and from that of the solar/planetary system. In addition, the definition of what Newton called “gravity” is rooted in the relation of all orbital motion to Kepler’s third law. Kepler’s third law (α=R3/T2) and Sir Newton’s law of gravitational attraction (F=-GMm/R2) are fundamental references for orbital motion. After the full derivation, it is also shown that the coulomb force of attraction (F= -q2/(4πεoR2)) in the hydrogen atom yields a significantly same result as the Newtonian force of attraction between the proton and electron in the hydrogen atom, with a gravitational constant of 7.55 × 1028 N.m2.kg-2. It is shown that the unifying gravitational constant for all matter of nature is G=Z/A {1.525 1892 × 1029} N.m2.kg-2. It is further hypothesised, based on the outcome of the theoretical derivation and correlation of the results between the coulomb and gravitational forces that gravity is electrostatic in nature and that they are reciprocally special cases of the general formula derived and presented in this paper.
The conclusions drawn from the results are supported by the analyses of information, using existing solar system/planetary data and atomic physics data. The results were correlated and confirm the hypotheses.
Relativity • Gravitational constant • Newton’s gravitational law • Coulomb’s electrostatic law • Classical mechanics • Quantum mechanics • Schrodinger’s equation • Solar system • Astrophysics • Planetary motion • Periodic table of elements • Gravitational constants of elements and planetary masses • Atomic interactions • Space time • Kepler’s laws • Mean planetary distance from the Sun • Orbital radius • Period of orbital revolution • Dimensionless numbers of nature • Large numbers of nature • Gauss’ theorem • Gaussian surface
A: Relative Atomic Mass Number, r.a.m; amu: atomic mass unit, 1.660 538 921 x 10-27 kg; AU: Astronomical Unit, based on the mean distance between the sun and earth; CoM: Centre of Mass; E: Energy eigenvalue of the state of the quantum mechanical wave function, ψ (r, t); G: Newton’s gravitational constant, 6.674 28 × 10-11 N.m2.kg-2; Gf: Relative gravitational constant, (Z/A)*(1.5251892 × 10+29) N.m2.kg-2; H: Hamiltonian in classical mechanics=T+V=(Kinetic Energy) + (Potential Energy) Ĥ: Hamiltonian operator in quantum mechanics; Mi: Mass of the central body orbited by other bodies of mass mi (e.g. Sun, Earth or Nucleus); Mn: Molar mass of substance; mi: Mass of planet i; me: Mass of electron, 9.109 382 91 × 10-31 kg; mn: Mass of neutron, 1.674 927 351 × 10-27 kg; mp: Mass of proton, 1.672 621 777 × 10-27 kg; NA: Avogadro’s Constant, NA=6.022 141 × 1023 atoms.mol-1; n: Principal quantum number; nm: number of moles of an element/substance=m/Mn; p: Momentum; q: C; R: Radial centre-to-centre distance from the central body Mi (CoM) to the orbiting body, mi (CoM); R: Radial vector (x, y, z); ri: Radius of planet i (x, y, z); r: radial vector of planet i, ((x, y, z); Ti: Orbital period of planet or orbiting mass, mi around the central body, Mi; Z Atomic number; ωi: Angular speed of Planet mi around the central body; α:used to define Kepler’s 3rd Law as α=R3/T2; β: used to express the value of the relation between G=β (4πεo); δ: used to express the value of the relation between G= δ (q2/4πεo); ∇2: Del-squared or Laplacian Operator; εo: permittivity of free space; π: 3.14159265359; θ angle in radians or degrees, as specified; λ wavelength; ρ: density of matter; ψ; wave function, ψ (r, t);
Johannes Kepler empirically derived three laws from the data initially compiled by Tycho Brahe. Brahe made his observations without the use of a telescope [1]. Kepler’s third law which states that: The ratio of the cube of the orbital radius from the centre of the revolving object to the centre of the central body divided by the square of the corresponding orbital period is constant, herein denoted as α=R3/T2, is fundamental to gravitational postulations, derivations and calculations.
Based on Kepler’s laws, sir Newton followed with principia mathematica, including the derivation of F=ma (mass × acceleration) and developed the inverse square law of gravitational attraction, taking into account the centripetal force (mv2/R or m ω2R) and the central force of gravity (F=-GMm/R2), which led to the empirical determination of the gravitational constant, G. Up to the writing of this paper, we used G as the universal constant for the determination of the gravitational potential and force of attraction between two objects of mass, Mi and mj and a centre to centre distance R apart.
For over 330 years, since Newton’s derivation and naming the phenomenon “gravity”, scientists have been searching for the origin of gravity and the unification of the four fundamental forces of nature, being: the strong and weak forces, and the electromagnetic forces and gravity [2]. A study of Newtonian gravity measurements which imposed constraints on unification theories, found that such constraints were not viable [3]. Furthermore, using the gauge theory and “standard model”, the unification of electromagnetic and weak forces has been treated [4]. However, the unification of gravity with electromagnetism/electrostatics remained unresolved up to the presentation of the hypothesis and derivations in this paper.
During the 20th century Einstein (1916) introduced General Relativity (GR), as a theory for us to describe gravity in terms of the curvature of space time. In addition to the famous E2=m2c4 + p2c2 equation, Einstein developed the well-known GR equation.
To date, that GR equation is applied to describe gravity as the curvature of space-time. The proposition in this paper is that G is not constant in all frames of reference, but is relative to the centricity of orbital motion. Furthermore, it will be shown in this paper that gravity is electrostatic in nature and related to electromagnetic fields as also supported in. While Coulomb’s law is an experimentally determined result, a fundamental theoretical model will be derived in this paper, which will also account for Newton’s law of gravitation [5].
In this paper I take cognizance of the scientific principles necessary to present information and findings. In order not to clutter the derivations with vector notations and center of mass provisions in the derivations, I will present the derivations in scalar format and treat the mass of the heaviest body in the analysis as the CoM. It is also the purpose of this paper to present the hypotheses which are intended to lead us closer to a better understanding of how the universe works, by showing the relative nature of the gravitational constant, gravitational field, potential and force of attraction. It is also shown that it correlates with Coulomb force of interaction, not only in terms of similarity of principles or formulae but with regard to the actual natural phenomenon, the formulae and the calculated results. It will become evident that what we historically applied as the universal gravitational constant in all frames of reference, is in fact relative and applicable to a frame of reference in which 4π2R3/MT2 is constant and equivalent, allowing for statistical deviations of the calculated mean constant, G, for large Masses (M). The results will show that G is more specific in quantum mechanics to atomic nuclei, for each periodic table element and that the proton is a key gravitational particle. The question as to whether G is universal or not was already raised but remained unresolved [6].
Hypotheses
The following hypotheses are formulated to test the validity of the competing claims. The H0 (Null Hypothesis) being the status quo and which may be rejected when H1, H2, H3 (Alternative Hypotheses) are tested and provide supporting results to reject H0:
H0: Is the gravitational constant, G, universal and applicable to all frames of reference, where bodies, mi, are in orbital motion and revolving a central body, M, and to determine the gravitation potential and force of attraction between the two bodies, M and m?
Is G=6,674 × 10-11 (N.m2.kg-2) universal, because the ratio R3/T2 is constant and equal in all frames of reference?
H1: Is the gravitational constant, G, speci ic to the respective frame of reference of the central body, M, orbited by the other bodies, mi, in the particular orbital system of the central body?
Is the ratio R3/T2 constant in a speci ic frame of reference, but not equal across all frames of reference. Hence, is G ≠ 6,674 × 10-11 (N.m2.kg-2) in all reference frames?
H2: Is there a relation between Kepler’s 3rd law R3/T2 and the quantum composition of matter, such that the central body, M, can be inferred by applying the gravitational constant formula for M=4π2R3/GT2 based on the bodies, mi, revolving the central body, M?
H3: Is the gravitational force of attraction an electrostatic/ electromagnetic force, based on the intrinsic (constituted of protons, neutrons and electrons) nature of all matter? Is it expected that there is a relation between G and q2/4πεo, such that G=δq2/4πεo where: δ a value to be determined by way of derivation and computation, from fundamental principles of physics? εo is the permittivity of free space [7].
In order to develop, determine and test the validity and applicability of the respective hypotheses, it is important for us to revert to the original Newtonian definition and derivation of the gravity law and the resulting gravitational constant based on Kepler’s 3rd law. The results should be congruent with existing laws and theories and produce testable predictions of the various interactions from planetary bodies to quantum mechanics.
During February 2022, I released a media statement which specified the result for the relative gravitational constant at atomic level, for hydrogen (2H-Deuterium), to be 7.55 × 1028 N.m2.kg-2 by applying the readily available empirical data for the 2H atom. To advance the significance of that result, it is also essential to derive and show the general result which is applicable to all elements of the periodic table, as well as the planetary system. Therefore, the derivations of the following key equations for planetary and atomic interactions were analysed: a) R3/T2; b) 4π2R3/MT2; and c) δ q2/4πεo. EXCEL Spreadsheets and readily available planetary and atomic data were used for the calculations. The source data for the planets was obtained from tables in Walker and Spiegel for atomic data from the Particle Physics Booklet and tables in Wong. The computed results were compared to the current Newtonian gravitational constant, G=6.674 28 × 10-11. The three frames of reference, namely:
• The sun as the central body, M;
• The Hydrogen (Deuterium 2H) nucleus as the central body, M;
• The earth as the central body, M for the moon orbiting the earth, forms the basis of the hypotheses tests.
It is worthwhile to note that, at the time of the development and presentation of the gravitational law of attraction in 1687, Sir Newton did not have access to some of the subsequent laws and theories such as those of Coulomb’s inverse square law of electrostatic attraction and repulsion, as well as other theoretical developments from Dalton, Avogadro, Thomson, Millikan, Rutherford and Bohr, Chadwick and many other theories of atomic physics, nuclear physics, electromagnetism and quantum mechanics. Similarly, the model of the atom was not fully developed when Einstein published the general theory of relativity. Newton named the observed phenomenon “gravity”.
Assumptions and data analyses of planets, the moon and the hydrogen (2H) atom
The following main assumptions are considered to ensure that the consistency of analyses, validity, rigour and vigour are not compromised:
That the data utilized is related to the extent of planetary, near earth and atomic data available and significant enough to test the hypotheses, so as to draw material conclusions; that the information and data obtained from long established and utilized physics textbooks are accurate enough for the purpose of the hypotheses to be tested, without limitation to any other reliable source data that may be used by the reader; that the variations in data between the sources are not significant; that significant numbers are not emphasised, but are only distinguished as far as indicating the principle which needs to be reconfirmed or fundamentally revised; that based on the data sample sizes, where applicable and less then n=50, the t-distribution will be utilised for calculations of descriptive statistics and significance.
That for purposes of simplified algebra the respective central masses, Mi, being orbited are treated as the CoM, as each is more than 98% of the total mass of the respective system: Sun (99.8%), earth (98.7%) and deuterium-2H nucleus (99.9%) [8].
Table 1 below contains the data used to calculate, analyse and test the alternate hypotheses, H1, H2 and H3.
| A: Planetary | |||||||||
| # | Mi | Ri km x 106 | Ti (earth yr) | Vi(km/s) | R3/T2 | 4π2R3/MT2 | |||
| 1 | Mercury | 58.20 | 0.241 | 47.90 | 3.4329E+18 | 6.8137E-11 | |||
| 2 | Venus | 108.00 | 0.615 | 35.10 | 3.3686E+18 | 6.6861E-11 | |||
| 3 | Earth | 150.00 | 1.00 | 29.80 | 3.4135E+18 | 6.7752E-11 | |||
| 4 | Mars | 227.00 | 1.88 | 24.10 | 3.3472E+18 | 6.6437E-11 | |||
| 5 | Jupiter | 778.00 | 11.86 | 13.10 | 3.3860E+18 | 6.7208E-11 | |||
| 6 | Saturn | 1427.00 | 29.46 | 9.65 | 3.3863E+18 | 6.7213E-11 | |||
| 7 | Uranus | 2871.00 | 84.00 | 6.80 | 3.3921E+18 | 6.7327E-11 | |||
| 8 | Neptune | 4 498.00 | 164.80 | 5.44 | 3.3890E+18 | 6.7266E-11 | |||
| 9 | Pluto | 5910.00 | 248.40 | 4.75 | 3.3836E+18 | 6.7160E-11 | |||
| Average, μ | 3.3888E+18 | 6.7262E-11 | |||||||
| STD, σ | 2.4343E+16 | 4.8318E-13 | |||||||
| B: Atomatic (Hydrogen Atom) | |||||||||
| # | mi | Ri m x 10-12 | Ti (S) | Vi (km/s) | R3/T2 | 4π2R3/MT2 | |||
| 10 | Hydrogen | 52.8 | 1.52E-16 | 2187.279 | 6.3986 | 7.5460E+28 | |||
| C: Moon (Orbiting the Earth) | |||||||||
| # | mi | Rim x 106 | Ti (earth yr) | Vi (km/s) | R3/T2 | 4π2R3/MT2 | |||
| 11 | Moon | 0.384 | 0.07479 | 1.02 | 1.02371E+13 | 6..7583E-11 | |||
• Planetary data is for planets orbiting the sun, including the dwarf planet Pluto.
• Atomic (Hydrogen Atom) data, as the hydrogen atom forms the basis for many of our insights into atomic and nuclear mechanics.
• Moon (orbiting the Earth) data, as the closest permanent companion of the Earth, which also provides us with invaluable clues into the planetary system.
The computed results in Table 1, p.10, reveal the following important information.
For H1: In congruence with Kepler’s third law, the ratio R3/T2 for each planet in the solar system, including the dwarf planet Pluto which also orbits the sun is equal to 3.3888 × 1018 ± 0.024343 × 1018; for the 2H-Deuterium atom, the ratio, R3/T2=6.39; for the earth orbited by the moon, the ratio R3/T2=1.023 × 1013; based on the available sample data utilised, the Keplerian ratios are specific to their frames of reference and signi icantly different. Thus, reject H0 and accept H1.
For H2: The ratio R3/T2 for the sun (as central body, M) is not equal to the respective ratios of the moon orbiting the earth (as central body M), as well as the electron orbiting the Hydrogen nucleus (as central body M); The ratio R3/T2 changes significantly from Helio-centric orbits to geo-centric orbits to the nuclei-centric orbits. The values of the ratios between the three (3) categories of Table 2 being:
| A (Planets) | C (Moon) | B (2H Atom) |
|---|---|---|
| 3.3888 × 1018 | 1.02371 × 1013 | 6.398562 |
| 5.296 × 1017 | 1.5999 × 1012 | 1 |
In further support of sir Newton’s law of gravitational attraction, the average G in the solar system is calculated to be 6.7262 × 10-11 ± 0.048318 × 10-11. This constant, as formulated by sir Newton, is within material range (± 0.77309 %) of the internationally accepted (SI) value of G=6.6742 × 10-11.
The gravitational constant of attraction of the earth (as central body, M) on the moon is calculated from the data to be Gearth=6.7583 × 10-11. This value of G is also within material range (± 1.2600 %) of the internationally accepted (SI) value of G=6.6742 x 10-11.
However, the gravitational constant of attraction, using the data in Table 1, for atomic nuclei, in this case 2H-Deuterium-Hydrogen (Z=1, M=mp+mn), was found to be Gatomic=7.55 × 1028 which is materially different from the G for the sun or the earth [9].
Based on the available sample data utilized, the gravitational constant is different in different frames of reference. Thus, reject H0 and accept H2.
For H3: Lastly, to test H3, the relation between G=δq2/4πε0.
Initially, G=β (4πε0) was calculated and found to be β=0.599721,
such that G/4πε0=0.599721 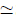 3/5. This result interestingly resembled
the factor sued in the coulomb calculations in nuclear physics, except
that in this case β is not dimensionless, but merely providing a much
reduced relational number, which may be interpreted and understood
in future work.
3/5. This result interestingly resembled
the factor sued in the coulomb calculations in nuclear physics, except
that in this case β is not dimensionless, but merely providing a much
reduced relational number, which may be interpreted and understood
in future work.
From 5.7 above and the coulomb energy Vc = 3/5 (1/4πε0) (Ze2/R)
for a spherical nucleus and assuming that the charge is distributed
spherically. Nature gives us the clue of the likely relation between
gravitational potential and electrostatic potential following the
observation that the same factor appears in the coulomb energy for
the nucleus. The relation between the gravitational law and the
electrostatic law was also investigated and the resulting “…
gravitational constant G is expressed exactly through the elementary
charge e and the electromagnetic vacuum constants ξ, ε0 and μ0”,
and the resulting dimensionless constant in that derivation,
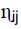 (=4.39
× 10-40), is speci ic to magnetic moment of interacting particles.
Further generalisation is required to account for the quantum physical
composition of different matter, from subatomic particles to large
masses and constellations.
(=4.39
× 10-40), is speci ic to magnetic moment of interacting particles.
Further generalisation is required to account for the quantum physical
composition of different matter, from subatomic particles to large
masses and constellations.
In addition to the relation asserted, I derive the following expanded relation to show that in the coulomb experiment, certain variables were implicitly incorporated in the experimentally determined law. The formulation is as follows:
Original coulomb’s law: F=Q1Q2/4πε0R2
Additions to the above equation:
The charges Q1 and Q2 are either added or removed from objects of mass m1 and m2, respectively to attain the net charge on each object.
The masses m1 and m2 are constituted of their respective atoms (protons, neutrons and electrons) as:
m1= {A1 × (a.m.u.) + Z1me} × (NA × nm1);
m2= {A2 × (a.m.u.) + Z2me}× (NA × nm2);
Zi=The number of protons in the nuclei of the atoms of each mass;
Z × qp=Z × qe Charge conservation;
(Ai-Zi)=Neutrons in respective mass;
Applying Gauss’ Theorem (closed surface) on neutral mass, then:
For mass m1:
 =(+Z1qp-Z1qe) × NA1 × nm1/ε0=0
=(+Z1qp-Z1qe) × NA1 × nm1/ε0=0
For mass m2:
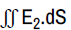 = (+Z2qp-Z2qe) × NA2 × nm2/ε1=0
= (+Z2qp-Z2qe) × NA2 × nm2/ε1=0
Applying Gauss’ Theorem (closed surface) when charge has been added or removed:
For mass m1: example of +ve charge: (X number of –ve charges)
For an object to be +vely charged, electrons are removed. Thus, 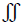 E.dS=(+Z1qp-Z1qe) × NA1 × nm1-(-X1qe)/ ε0=+X1qp/ ε0
E.dS=(+Z1qp-Z1qe) × NA1 × nm1-(-X1qe)/ ε0=+X1qp/ ε0
The new mass (m1)’ = {A1 × (a.m.u.) + Z1me} × (NA × nm1) – X1me; For mass m2: example of -ve charge: (Y number of -ve charges)
For an object to be -vely charged, electrons are added. Thus, 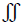 E.dS=((+Z2qp-Z2qe) × NA2 × nm2-(-Y2qe)/ ε0=Y2qp/ ε0
E.dS=((+Z2qp-Z2qe) × NA2 × nm2-(-Y2qe)/ ε0=Y2qp/ ε0
The new mass is (m2)’ = {A2 × (a.m.u.) + Z2me}× (NA × nm2) + Y2me;
Applying “specific charge” relation for a negative and positive charges to quantized mass in relation to charges:
For an electron: -qe/me
For a proton: +qp/mp=+qp/A (a.m.u)
Having introduced the above context of the relation of specific charge (charge and mass), I now revert to Coulomb’s Law (in this example for m1 +vely charged and m2 –vely charged, but can be generalized) and apply lines 5.8 to 5.12 as follows:
F=Q1Q2/4πε0R2 = (+X1qp) (-Y2qe)/4πε0R2
F= (+X1 mp (qp/mp)) (-Y2me (qe/me))/4πε0R2
F=(+X1 mp (qp/A (a.m.u.)) (-Y2me (qe/me))/4πε0R2
Rearranging the above equation, as follows:
F=(qp/A (a.m.u)) (qe/me)/4πε0 R2 (+X1mp) (-Y2me)
F=(1)/A (1)/4πε0R2(qp)(qe)/ a.m.u.) (me) (+X1mp)(-Y2me)
F=(1)/A(1)/4πε0R2(qp)(qe)/ a.m.u.) (me) (+X1mp)(-Y2me)/R2
This equation includes the Coulomb variables of charge and radial distance, as well as the Newtonian variables of mass and radial distance.
Based on the above derivation and correlation of coulomb’s electrostatic law with Newton’s gravitational law, there is a relation between the two fundamental laws of nature. Thus, reject H0 and accept H3.
Following the above generalized formulation of coulomb’s law and the observation that Coulomb’s law and Newton’s law are fundamentally connected, except that for gravity the large masses are attracting each other, as opposed to quantum particles which can attract or repel each other, depending on the net Gaussian charge. Based on this important connection, the derivation of the relative gravitation constant, G=4π2Ry/MT2, which is applicable to all bodies from planetary, solar to atomic level (2H-Deuterium) atom is provided as follows, before generalization:
From:
Force (F)=mass (m) × acceleration (a)=mv2/R
F=Zq2/4πε0R2
m=mass of the electron in orbit.
mev2/R=Zq2/4πε0 R2
me (2πR/T)2/R=Zq2/4πε0 R2
mevRn=nh/2π (Bohr Postulate) and p=mev=h/2πRn/n=h/λ (de Broglie Postulate)
After substitution and rearrangement, we have:
n=Principal quantum number;
Rn=n2h2ε0/Zq2mπ=n2/Z RB; where RB is the Bohr Radius.
Then:
From the Bohr quantum condition and de Broglie condition for angular momentum, L: L=Rn × pn=mvnRnsin (90o)=nh/2π
We find v: vn=nh/2πmR
Using vn and Rn, m=me we ind the orbital period, T: Tn =2πR/v
Substituting vn and Rn, we ind the orbital period,
Tn: Tn=2πRn/vn=2πR/nh/2πmeRn=(2πR/1) (2πmeRn/nh)=4π2 me (Rn)2)/nh
Then from the semi-classical approach using Kepler’s 3rd Law we find R3/T2 by substituting T with Tn and R with Rn, the result is:
(Rn)3/T2=((n2 h2ε0/Zq2meπ)3/(4π2 me(Rn)2)/nh)2=(n8h8(ε0)3/ (16Z3q6(me)5(π)7(Rn)4
=(n8h8 (ε0)3/ (16Z3q6 (me)5(π)7(n2h2ε0/Zq2meπ)4=Zq2/16meπ3ε0
=Z (6.414095)
R3/T2=Z (q2/16mπ3ε0
Furthermore, it is fundamental for us to apply Sir Newton’s derivation and definition to determine the gravitational constant, G: G=4π2R3/MT2
M is the mass of the atomic nucleus, based on the similar principal to the mass of the central body which is being orbited. The nuclear mass constitutes 99.9% of the mass of an atom. In the case of atomic nuclei, the mass, M is:
M=Relative atomic mass number (A) x atomic mass unit (a.m.u)
M=A (a.m.u.)
After substituting the results of R3/T2 and M in G =4π2R3/MT2, we ind (the “-“sign is added to indicate the attractive nature of (-q2)= (+q)* (-q)):
G=-Zq2/A (a.m.u.) m4πε0
After rearranging the above equation of G and will herein forward referred to as relative gravitational constant Gf, or Gatomic we find:
Gf=-Z/A{1/4πε0}{q/a.m.u.)}{q/m}
=-Z/A {1.525 189 2 × 1029} N.m2.kg-2
The above result for Gf clearly shows that gravity is: electrostatic in nature based on the interactions of charges, +q and -q. Hence, the reference to gravitational field; relates to the specific charges of the electron {-q/m} and nucleon {+q/a.m.u)} depends on the ratio of Atomic Number (Z): Relative Atomic Mass Number (A). Each periodic table element has a gravitational constant based on its respective nucleon composition, as given in Appendix A. The ratio of Z: A gives a likely correlation to nuclear stability, since the relative gravitation constant reduces with decreasing Z/A factor, as depicted.
The above results indicate that Gf is not constant across all frames of reference. The aforementioned derivations, results and observations are significant, as they unify Coulomb’s law and Newton’s gravitational law as interactions of the same fundamental phenomenon [10].
Following the above derivation of Gf, the Newtonian gravitational potential and Coulomb electrostatic potential are unified into one fundamental equation as:
V(R) =-Zq2/A (a.m.u.) m4πε0 Mm/R
As a result of the above generalised potential ield, the Coulomb potential energy equation in the Schrodinger equation is unified with the Newtonian gravitational energy equation, such that the Hamiltonians in the TDSE (Time Dependent Schrodinger Equation) and TISE (Time Independent Schrodinger Equation) can be substituted with the generalised potential equation:
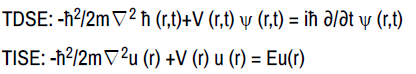
Such that:
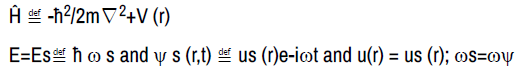
Theoretical and empirical analyses
Utilizing the results computed in Table 1, p. 10, and the observations in section 5 above, the following further calculations were made to draw conclusions and make propositions based on the results of the theoretical and empirical analyses:
Firstly, the gravitational constants, as calculated in section 4, are applied as per the usual analytic process in the frames of reference of the Sun, Earth and nuclei as central bodies [11].
Secondly, the hypotheses, in section 2, are applied and tested.
The results are as presented in Table 3 below:
| # | mi (Name) | Ri km x 106 | Ti(earth-yr) | Vi(km/s) | R3/T2 (m3/s2) | 4π2R3/MT2Gs | mi (kg) | Sun(acc.) Gs.Ms/R12 | ForceG (N) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Mercury | 58.2 | 0.241 | 47.9 | 3.4329E+18 | 6.8137E-11 | 3.20E+23 | 4.0010E-02 | 1.2803E+22 |
| 2 | Venus | 108 | 0.615 | 35.1 | 3.3686E+18 | 6.6861E-11 | 4.90E+24 | 1.1401E-02 | 5.5867E+22 |
| 3 | Earth | 150 | 1 | 29.8 | 3.4135E+18 | 6.7752E-11 | 5.98E+24 | 5.9893E-03 | 3.5816E+22 |
| 4 | Mars | 227 | 1.88 | 24.1 | 3.3472E+18 | 6.6437E-11 | 6.40E+23 | 2.5644E-03 | 1.6412E+21 |
| 5 | Jupiter | 778 | 11.86 | 13.1 | 3.3860E+18 | 6.7208E-11 | 1.90E+27 | 2.2085E-04 | 4.1961E+23 |
| 6 | Saturn | 1427 | 29.46 | 9.65 | 3.3863E+18 | 6.7213E-11 | 5.70E+26 | 6.5651E-05 | 3.7421E+22 |
| 7 | Uranus | 2871 | 84 | 6.8 | 3.3921E+18 | 6.7327E-11 | 8.70E+25 | 1.6246E-05 | 1.4134E+21 |
| 8 | Neptune | 4498 | 164.8 | 5.44 | 3.3890E+18 | 6.7266E-11 | 1.03E+26 | 6.6129E-06 | 6.8113E+20 |
| 9 | Pluto | 5910 | 248.4 | 4.75 | 3.3836E+18 | 6.7160E-11 | 5.40E+24 | 3.8245E-06 | 2.0652E+19 |
| 10 | Average, µ | 3.3888E+18 | 6.7262E-11 | ||||||
| B: | Atomic | (Hydrogen Atom) | Ma (kg) | 3.35E-27 | Gravitational | Law | |||
| # | mi (Name) | Ri m × 10-12 | Ti(s) | Vi (km/s) | R3/T2 (m3/s2) | 4π2Ra3/MaTa2 Ga | me-and (kg) | Gi (acc.) Gi.Ma/R2 | ForceG (N) |
| 11a | Hydrogen | 52.8 | 1.52E-16 | 2187.279 | 6.3986 | - | 9.11E-31 | 8.08E-17 | 7.36E-47 |
| 11b | Hydrogen | 52.8 | 1.52E-16 | 2187.279 | 6.3986 | 7.55E+28 | 9.11E-31 | - | 8.25E-08 |
| B1: | Atomic | (Hydrogen Atom) | Qa (C) | 1.60E-19 | Coulomb's | Law | |||
| # | Qe- (Name) | Ri m × 10-12 | Ti (s) | Vi (km/s) | R3 /T2 | 4π2Ra3/MaTa2 Ga | qe- (c) | Coul. Constant 1/4 πε | Forcec (N) |
| 11c | Hydrogen | 52.8 | 1.52E-16 | 2187.279 | 6.3986 | - | 1.60E-19 | 8.99E+09 | 8.28E-08 |
| C: Moon | (orbiting | the Earth) | ME (kg) | 5.98E+24 | |||||
| # | mi (Name) | Ri km × 106 | Ti (earth-yr) | Vi(km/s) | R /(m3/s2) | 4π2Ra3/ MT2GE | mi (kg) | Earth (acc) Gs.ME/Ri2 | ForceG (N) |
| 12a | Moon | 0.384 | 0.07479 | 1.02 | 1.02E+13 | 7.38E+22 | 0.002728 | 2.01E+20 | |
| 12b | Moon | 0.384 | 0.07479 | 1.02 | 1.02E+13 | 6.76E-11 | 7.38E+22 | - | 2.02E+20 |
The results computed and listed in Table 3 above, show several important outcomes. The observations are listed as follows:
Coulomb’s electrostatic law and sir Newton’s gravitational law are fundamentally of the same natural phenomenon. Hence, their similarity in formulation;
It is therefore proposed that the model for the unifying electrostatic/gravitational field equation be:
Unifying potential: V (R)=-Z/A {1/4πε0} {q/a.m.u.)} {q/m} Mm/R
For coulomb’s law: V (R)=-Z/A {1/4πε0} {q/ (1)} {q/1}1/R (opposite charges)
Where I observe that: A=1, a.m.u=1, M=1 and m=1 is an implied special case of the general gravitational equation.
Planetary gravitational analyses:
Gravitational law: V=-Z/A {1/4πε0}{q/a.m.u.}{q/m} Mm/R
Where G=6.674 28 × 10-11 N.m2.kg-2 is a special case of the general gravitational formula:
G=-Z/A{1/4πε0}{q/a.m.u.}{q/m}
Such that solving for Z/A, we obtain:
6.674 28 × 10-11 = Z/A {1/4πε0}{q/a.m.u.}{q/m}
=Z/A {1.5251892 × 1029} N.m2.kg-2
Resulting in: Z/A =4.376 03413 x 10-40=1/2.285174 x 1039
Observations
From the above results, an important observation is made that the special dimensionless large number (2.285 174 × 1039) in the denominator of Z/A indicates the ratio of the number of nucleons for each proton in the planetary masses. This ratio may not necessarily be the same for all large masses, leading to different gravitational interactions. The above mentioned large number (2.285 174 × 1039) used to be the unknown factor whenever the strength of the Coulomb force was compared to the strength of the gravitational force. It follows from the above result that the large number is as a result of the ratio of protons (Z) to the number of nucleons (A) in the mass of the central body, M, in this case the sun. By applying Newton’s gravitational constant for the sun at atomic for quantum mechanical interactions was an implicit assumption that the ratio of Z: A is the same for all reference frames, while the Z: A ratios at atomic level are distinctly different for each periodic table element. The aforesaid application of the Newtonian gravitational constant in quantum mechanics also led to the disparities in observations between the predictions of interactions at planetary level and interactions at atomic level. This resulted in the historic conclusion that gravity can be ignored in quantum mechanical analyses. This paper shows to the contrary, that gravity and electrostatic fields, force and potential are of the same origin and should produce the same or similar predictions and results for the respective orbital systems. It is evident from the result for Gf, in section 5 above, that the gravitational constant is relative to the centricity of orbital motion, based on the ratio of Z: A; The interpretation that gravity is the curvature of space-time is as a result of the influence and effect of the electrostatic field in space-time between masses. The orbital characteristics of planets around the sun and the earth show significantly comparable results for a similar gravitational constant, as listed in Table 2, lines 1-10 and 12a and 12b. Hence, we may apply the Newtonian constant G=6.6742 × 10-11 in calculations for interactions of bodies mi, in these two frames of reference, with minimal deviation; The gravitational constant for atomic nuclei, Gf (also referred to as Gatomic), based on the calculations for a Hydrogen (2H) atom, is distinctly different from that of the sun and earth, using empirical data:
G=Gsun (=6.6742 × 10-11) ≠ GEarth (6.7583 × 10-11) ≠ GDeuterium (7.55 × 1028)
The general gravitational constant is Gf=Z/A {1.5251892 × 1029} N.m2.kg2.
When the gravitational constant is calculated (using empirical data) based on the central body, Mi and the related orbital characteristics of the bodies, mi revolving around the central body, Mi, then a computed relative gravitational constant Gf constant is applicable in that particular frame of reference for all motion, as per Table 2, lines 1 to 10, 12a and 12b.
It is observed from the results in Table 2, lines 11a and 11b that when the Newtonian gravitational constant G, based on planetary motion is imposed in the atomic frame of reference, then the results for the calculation of the gravitational force of attraction on the orbiting electron are distinguishably and significantly different from the results of the Coulomb force of attraction. When the relative gravitational constant, Gf, is applied in any frame of reference and compared to the Coulomb force of attraction, then the results of the Newtonian and Coulomb forces correspond significantly, as shown in Table 2, lines 11b and 11c, to within margin of error of ± 0.2622% (8.254 × 10-8 N ± 0.2622%), using the readily available atomic data. By applying the general gravitational formula to the naturally abundant isotopes of the periodic table, a list of relative gravitational constants is provided for each element, as per appendix A, according to the distinct sequence of atomic numbers. In appendix B the elements are listed from the largest relative gravitational constant to the least, with the accompanying periodic Table of constants. It is observed that this list shows a trend of atomic nuclei stability, from the most stable nuclei to the least stable nuclei. There are a set of 6 elements from Z=78 to 83, namely: Pt (Z=78), Au (Z=79), Hg (Z=80), Tl (Z=81), Pb (Z=82) and Bi (Z=83) which are classified as naturally stable, but are among elements with unstable nuclei.
With the exception of Hydrogen (1H) with the highest relative gravitational constant of 1.513 13 × 10+29 N.m2.kg-2 as depicted in Figure 1, there is a similar range for the relative gravitational constants of the remaining elements from O (Z=8) at 7.626 23 × 10+28 N.m2.kg-2 to the lowest for U (Z=92) at 5.894 97 10+28 N.m2.kg-2.
Figure 2 depicts the inverse reduction trend of the relative gravitational constant per nucleon plotted versus the atomic number of the periodic table elements.
A further important result of the general gravitational derivation is that:
All orbital motion obeys Kepler’s 3rd law and the universal relation is: R3/T2=Z (q2/16mπ3ε0)=Z (6.414095)
The above result may be applied to new astrophysics observations of galaxies. The results for Z from the data for the planets orbiting the sun are listed in Table 4 below:
| A: Planetary | 6.414095 | 1.53E+29 | |||
| # | mi | Fixed | Fixed | ||
| (Name) | then Zsun | then Aempirical | "Z/A" | Inverse of "Z/A" | |
| 1 | Mercury | 5.35E+17 | 1.20E+57 | 4.47E-40 | 2.24E+39 |
| 2 | Venus | 5.25E+17 | 1.20E+57 | 4.38E-40 | 2.28E+39 |
| 3 | Earth | 5.32E+17 | 1.20E+57 | 4.44E-40 | 2.25E+39 |
| 4 | Mars | 5.22E+17 | 1.20E+57 | 4.36E-40 | 2.30E+39 |
| 5 | Jupiter | 5.28E+17 | 1.20E+57 | 4.41E-40 | 2.27E+39 |
| 6 | Saturn | 5.28E+17 | 1.20E+57 | 4.41E-40 | 2.27E+39 |
| 7 | Uranus | 5.29E+17 | 1.20E+57 | 4.41E-40 | 2.27E+39 |
| 8 | Neptune | 5.28E+17 | 1.20E+57 | 4.41E-40 | 2.27E+39 |
| 9 | Pluto | 5.28E+17 | 1.20E+57 | 4.40E-40 | 2.27E+39 |
| Average, μ | 5.28E+17 | 1.20E+57 | 4.41E-40 | 2.27E+39 | |
All gravitational interactions may be derived from the general gravitational potential energy equation:
V=-Z/A {1/4πε0}{q/a.m.u.}{q/m}Mm/R
=-Z/A {1.5251892 × 1029} Mm/R
From the above general gravitational potential energy equation, I observe that in the absence of a proton in any of the interactions between masses or particles, the gravitational interaction will be zero. The following set of equations is provided in support of this observation, depending on the radial distance R between the particles:
Fe-e= -o/A {1.5251892 × 1029} meme/R2=0
Fn-n=-0/2.01733 {1.525189 ×1029} mnmn/R2=0
Fn-e=-0/1.008665{1.525 1892 × 1029} mnme/R2=0
Fp-e=-1/1.007825{1.525 1892 × 1029} mpme/R2 ≠ 0
Fp-n=-1/2.014102{1.5251892 × 1029} mpmn/R2 ≠ 0
Fp-p= -2/2.014552{1.525 1892 × 1029} mpmp/R2 ≠ 0
This study into the relative nature of the gravitational constant has provided material insight into the specific use of the computed gravitational constant, for a particular frame of reference.
The research was limited in the sense that only the readily available planetary data and that of the Hydrogen atom were utilized. More analyses may be carried out on other elements to evaluate and assess predictions as part of the work towards a Grand Unification Theory (GUT) and to compare with empirical results. However, based on the results computed and tabulated in Tables 1-3, as well as the observations made, it is my proposition that the gravitational force of attraction is electrostatic in nature, and by applying the relative gravitational constant principle we should be able to reciprocally determine the corresponding or equivalent and net covalent charge as well as corresponding magnetic fields of planetary bodies and other large bodies, based on their orbital characteristics and mechanics around a central body, Mi, similar to the interactions at atomic levels. Lastly, with these findings and other research work, we should be able to strive towards our quest for the unification of the four fundamental forces of nature, being: the strong and weak nuclear forces, electromagnetism and gravity and a better understanding of the universe as well as for further technological advancement.
Biosensors & Bioelectronics received 6207 citations as per Google Scholar report