Research Article - (2020) Volume 10, Issue 3
Received: 20-May-2020
Published:
12-Jun-2020
, DOI: 10.37421/jcde.2020.10.346
Citation: Shmeleva, Alisa A and Vyacheslav N Ivanov. “The Variation-Difference Method of Design of Shells with Normal Unconjugated Coordinate System and Design of Some Type of Surfaces for Checking of the Correction of the Program” Civil Environ Eng 10 (2020): 346 doi: 10.37421/jcde.2020.10.346
Copyright: © 2020 Shmeleva AA, et al. This is an open-access article distributed under the terms of the creative commons attribution license which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
At the classical literature of the design of the shell there is used the coordinated system of the middle surfaces of principle curvatures or common non-orthogonal coordinate system. The system of equations of the shells of complex forms is complicated and it’s difficult to receive the analytical decision. For analyses of the shells with non-orthogonal coordinate system and the most shells of complex form in the coordinate system of principle curvatures there is used usually finite element method which usually uses only the equation of the surface but don’t take into account the geometrical characteristics of the middle surfaces of the shell. At the chair of strength of materials and constructions of Engineering Academy RUDN there is worked up the complex program VRMSHELL for analyses of the shells of complex forms by variation-difference method. The complex includes the library of curves on the base of which there are calculated the geometrical characteristics of the classes of the surfaces included at the program complex. The complex includes the classes of surfaces as cylindrical, surfaces of rotation, Joachimsthal’s surfaces, Monge’s surfaces. The coordinate system of surfaces of these classes is the coordinate system of principle curvatures.
Normal cycle surfaces • Non-conjugated orthogonal coordinates • Thin-walled shells • Membrane theory of shells • Variation-difference method
In this article we investigated normal cycle surfaces. The normal cycle surfaces there are formed by moving of the circle of change or constant radius at the normal plane of the directrix, which is a line of the centers of the circles. The coordinate system of normal cycle surfaces is orthogonal but isn’t conjugated. The formulas of deformations of such type of shells differ of the analog formulas of shells with coordinate system of principle curvatures. On the base of investigation of the normal cycle surfaces there were made some modifications and class of normal cycle surfaces there was included at the program complex.
But the changing in complicated programs may put to some mistake and it’s necessary to check up the correction of the work of the program. It’s usually can be made by the comparison of the results received by the investigated program with the results received by analytical methods or by another program or the same program. In may be made by the same program but using another class of surfaces which gives the same form of shell [1-4].
At this work there are shown the peculiarity of design of shells with orthogonal non-conjugated system by variation-difference methods and there are given the example of design of stress-strain state of shells of rotation and tube shells. The shells of rotation are the normal cycle shell with strait line of centers and some decision may be received by analytical methods. The tube shells are the normal cycle shells with constant radius. Both of these types of shells enter to the class of Monge’s surfaces and the some calculations there were made by both blocks of the program complex.
The program complex VRMSHELL includes the library of curves. For every curve there are written the coordinate formulas and their derivation to third order. The new curves may be added at the library if it’s necessary. On the base of the library of the curves there are formed the sections of the shells according given parameters and calculated the geometrical characteristics and their necessary derivations at any point of the surfaces. These blocs of program there are written for every class of surfaces included at the program complex. It’s used the equations of directrix and generating curves of the concrete surface.
The variation-difference method there is based on the Lagrange’s principle – principle of minimum of the total energy of deformation [5]

E is a total energy of deformation; U is a potential energy of deformation; T is the work of external forces; δ is a symbol of variation of functional [6].
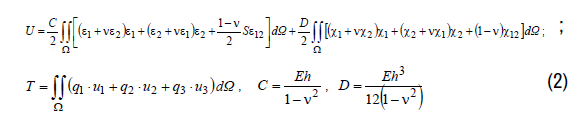
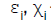 – tangential and bending deformations of middle surface of the shell;
Ni, Mi are tangential and bending forces; qi are the projections of loads at the surface coordinate system of the shell, ui are the displacements of middle
surface;
– tangential and bending deformations of middle surface of the shell;
Ni, Mi are tangential and bending forces; qi are the projections of loads at the surface coordinate system of the shell, ui are the displacements of middle
surface;  – parameter of the area of the middle surface.
– parameter of the area of the middle surface.
The section of the analyzed shell there is graduated by the net of equal or different paces. Using formulas of the numerical difference ratio with net displacements at the functional of total energy and minimizing it there is received the system of the algebraic equations. The decision of the equation gives web displacements at the nets of the shell. Using again the numerical difference ratios there are received the strains and further the tangential and bending forces and stresses. This bloc of the program is common but takes into account peculiarity of the class of the surface. The program there are realized the analyses of the sections of the shell with different condition of support and elastic supports and elastic foundation as well and on different types of loads. There may be analyzed shells with holes and shells with different contours.
Peculiarity of the normal cycle surfaces
The vector equation of the normal cycle surface with plane line of centers of generating curve (included at the program)

where  radius-vector of the surface;
radius-vector of the surface;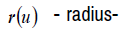 radiusvector
of the directrix line of centers of generating circles;
radiusvector
of the directrix line of centers of generating circles; 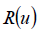 function of
radius of the generating circles;
function of
radius of the generating circles; 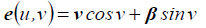 - equation of the
circle of unit radius at the normal plane of the line of the centers of the circles;
- equation of the
circle of unit radius at the normal plane of the line of the centers of the circles; 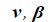 - vectors of normal and bi-normal of the line of circles; v- polar angle at
the normal plane of the of the line of the centers of circles.
- vectors of normal and bi-normal of the line of circles; v- polar angle at
the normal plane of the of the line of the centers of circles.
The geometrical characteristics of the surface:
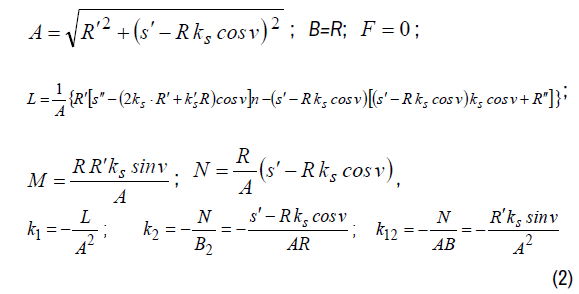
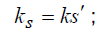 k - curvature of the directrix line;
k - curvature of the directrix line; 
 curvatures and twisting
curvatures and twisting
curvature of the normal cycle surface.
The coordinate system of normal cycle surfaces is orthogonal but isn’t conjugated so the generating circles aren’t the coordinates of principle curvatures of the surfaces.
The orthogonal coordinate system allows using the common Hooke’s law
and the formula of potential energy (2). But at the equation of deformations
must be used parameter of twisting curvatures 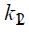 [7]:
[7]:
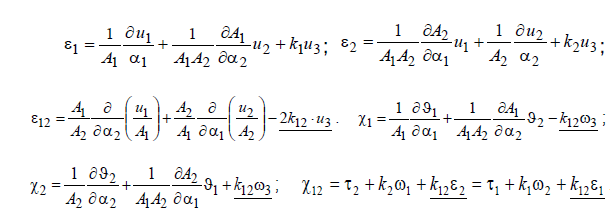
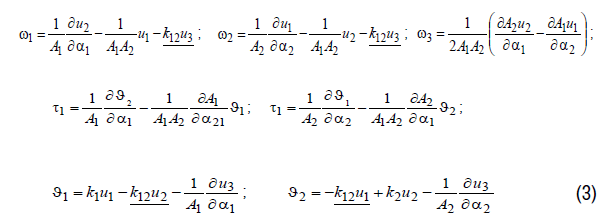
The analyses of stress-strain state of shell of revolution and tube shells on the base of block of normal cycle surfaces there has shown the near results with the results received by analytic analyses and analyses of the same shells made with the help of another blocks of the program complex. So this program block may be used for analyses of common types of normal cycle shells.
Journal of Civil and Environmental Engineering received 1798 citations as per Google Scholar report