Research - (2022) Volume 13, Issue 2
Received: 10-Feb-2022, Manuscript No. bej-22-54067;
Editor assigned: 12-Feb-2022, Pre QC No. P-54067;
Reviewed: 18-Feb-2022, QC No. Q-54067;
Revised: 24-Feb-2022, Manuscript No. R-22-54067;
Published:
28-Feb-2022
, DOI: 10.37421/2151-6219.2022.13.366
Citation: Hong Mao, Krzysztof Ostaszewski, Zhongkai Wen and Jin Wang. Time Inconsistent Stochastic Differential Game: Theory and an Example in Insurance. Bus Econ J 13 (2022): 366.
Copyright: © 2022 Ostaszewski K, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
In this paper, we study the retention and investment strategy in a time-inconsistent model for optimal decision problem under stochastic differential game framework. The investment portfolio includes multi-risky assets, whose returns are assumed to be correlated in a time-varying manner and change cyclically. The claim losses of insurance companies and investment are also assumed to be correlated with each other. Extended HJBI equations result in a solution to the portion of retention and an optimal portfolio with equally weighted allocations of risky assets, which is demonstrated first time theoretically. An optimal control bound is proposed for monitoring and predicting the optimal wealth level. The proposed model is expected to be effective in making decision for investment and reinsurance strategies, controlling, and predicting optimal wealth under uncertain environment. In particular, the model can be applied easily in the case of very high dimensional investment portfolio.
Stochastic differential game • Time-varying correlation • Extended HJBI equation • Equally weighted investment strategy • Investment and reinsurance
The optimal-decision problem in investment and reinsurance has attracted many attentions from academia and industry. Most literatures use time-consistent dynamic programming, establish, and solve Hamilton–Jacobi– Bellman (HJB) equations to obtain optimal solutions. Browne studied optimal investment decisions for a firm with an uncontrollable stochastic cash flow. Applied Cramer-Lundberg model for the risk process of an insurance company and used Geometric Brownian motion to model the investment in a risky asset (market index) from the surplus of the insurance company (as a measure of wealth of the insurance company). Studied optimal investment strategies for an insurance company receiving a constant-rate premium and used compound Poisson process to model the total claims to minimize the probability of ruin of insurance company. Browne (2001) studied two investors with different and possibly correlated investment opportunities under stochastic dynamic investment games in continuous time. The work of by introducing the worstcase portfolio optimization (with a market crash) in exponential utility of terminal wealth. Discussed the optimal proportional reinsurance and investment with multiple risky assets and no short positions.
Cao and Wan studied the optimal proportional reinsurance and investment strategies with Hamilton-Jacobi-Bellman equation. Minimized the convex risk of the terminal wealth of a market portfolio with a risk-free asset and a risky asset on a jump diffusion market under stochastic differential game. used similar stochastic differential game to model the relationship between an insurance company and the market; they used Max-Min strategy on the expectation for the utility of the terminal wealth to get the optimal investment and reinsurance strategy under uncertain environment. Applied the same differential game as in Zhang and Siu on the time-consistent optimization problem of retention and multiple-type loss-independent investment portfolio under uncertain environment. All the studies above have several limitations: (1) most of them considered only one risky asset and non-negative return rate due to the Geometric Brownian assumption for the return rate; (2) investment and the claim loss are considered to be independent processes except a few studies. Most of the previous studies applied time-consistent dynamic programming. However, it is usually the case that risky assets invested in capital market are correlated with each other; the investment returns are generally cyclical changing and can be negative sometimes, in fact, the return rates of investment funds in stock markets can be negative, especially at the time when economy experiences recession or crisis; the investment and claim loss may be correlated with each other; insurance companies are generally ongoing business and their surplus at terminal time is state-dependent and time-consistency is not satisfied due to non-Markovian setting.
The time-inconsistency of stochastic optimization problem is not allowed for a Bellman optimality principle. The following for the first time, proposed multi-variate Vasicek model with time-varying correlation for the return rates of multi-risky assets of Defined Benefit pension plan, but the time-inconsistency doesn’t play any role in their model. Obtained a general stochastic Hamilton-Jacobi-Bellman (HJB) equation for general coupled system of forward-backward stochastic differential equations with jumps. Applied timeinconsistent stochastic control in continuous time within a theoretical game framework and extended the standard Hamilton-Jacobi-Bellman equation to obtain the solution of the strategy and the value function at the equilibrium [1-22].
This paper establishes a time-inconsistent model under stochastic differential game framework with time-varying correlated risky assets. HBJI equation is established with loosened conditions of standard HBJI equation and state-dependent value function at terminal time. The solution of the extended HJBI equation results in optimal strategy of the portion of retention and equal weighted risky-asset investment. Control bound is proposed for monitoring and predicting the optimal wealth level for a finite time horizon. In fact, insurance companies are generally going concern businesses, and their life term is uncertain, hence it is difficult to determine their surplus at a terminal time. When wealth level is close to the lower bound or tends to move to the lower bound, the adjustment needs to be taken and new decision should be made based on the adjustment. The model presented in this paper is effective in the decision-making of investment and reinsurance strategies and in the control and prediction of optimal wealth under uncertain environment.
The remainder of this paper is organized as follows: section 2 gives the insurance and investment models; section 3 gives the extended Hamilton- Jacobi-Bellman-Isaacs (HJBI) equation and solution for the optimal investment and reinsurance strategies; section 4 presents results of our numerical analyses; section 5 concludes this paper.
The insurance and investment models
The following presents the notation we use:
C(t): Risk process of an insurer at time t
R(t): The surplus process (excluding investment) of insurance company at time t
α(t): The proportion of retention of proportional reinsurance at time t
p0: The net premium rate
δ: The safety loading of insurance premium
η:The safety loading of reinsurance premium
W1(t): The Brownian Motion for claim loss
W2(t): The Brownian motion for investment return rate
σD: The standard deviation of claim loss
αi(t): The proportions of the risky asset in investment portfolio at time t
Xt: the surplus or wealth of the insurer at time t
(t): the amount of risky-asset investment
rf: the risk free interest rate
ri(t): Return rate for risky assets i at time t
Let C(t): be modeled is a manner similar to Promislow and Young (2005):
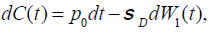 (1)
(1)
and let surplus process R(t) be modeled as
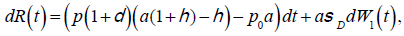 (2)
(2)
Where η ≥ δ.
Note that the Brownian motion model (continuous) of the claim process is the limit of the discrete compound Poisson model [8]. Borrowing at the risk-free interest rate is not allowed, i.e., Xt is not allowed to be negative for all t≥0, the amount invested in risky assets cannot be greater than the wealth level. Let (t) be the amount invested in risky assets.
Assume that the return process of risky asset ri(t) for i=1,2,…,n, at time follows the [23,24]. Stochastic process: π
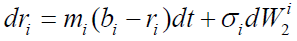 (3)
(3)
Where ri the return is rate of the i-th risky asset, and wi2 (t), i=1,2,…,n, are mutually dependent standard Wiener process defined on (Ω,F,{Ft}t≥0,P). For simplicity, it is assumed that the underlying filtration, Ft coincides with one generated by the Wiener process, that is, Ft =σ(W2(s):0≤s≤t) and σ denotes the volatility matrix.
If mi=m, then we have:
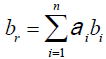 (4)
(4)
The return of investment portfolio can be described with Vasicek model as:
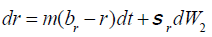 (5)
(5)
where σr is in instantaneous volatility of randomness measure of the return rate of investment portfolio, br is the long term equilibrium return rate of investment portfolio, br - r is the gap between its current rate of return and its long-run equilibrium level and m is a parameter measuring the speed at which the gap diminishes. The diversified portfolio consists of n types of risky investments, the fraction invested in i-th risky investment is ai, i=1,2,…,n, or α = (α1, α2, ...αn) and The return on risky asset i follows stochastic differential equation (3) and the return rate of the portfolio of risky assets is
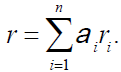 (6)
(6)
The differential of the portfolio return of risky assets is
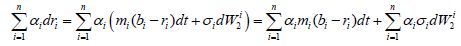 (7)
(7)
If the correlation between zi and zj, pij then the variance of the portfolio return is
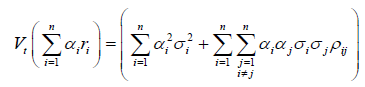 (8)
(8)
And the standard deviation is
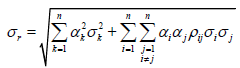 (9)
(9)
As in Momon (2004), the expected return rate of risky investment portfolio is
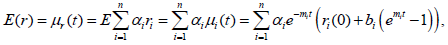 (10)
(10)
Where μi(t) is the expected return rate of i-th risky asset at time in real world measure and ri(0) is the return rate of i-th risky investment at t=0. Let
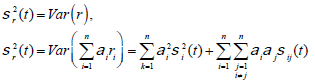 (11)
(11)
where σi2(t) is the volatility of the return rate of i-th risky asset under the real world measure,
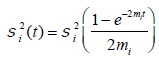 (12)
(12)
And σij(t) is covariance between i-th risky asset and j-th asset under the real world measure,
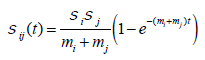 (13)
(13)
For the proof of equation (13), please see Appendix A.
Based on Mamon (2004), 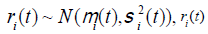 also satisfies
the stochastic differential equation:
also satisfies
the stochastic differential equation: 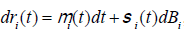 , where Bi is
i-dimensional standard Brownian Motion, i=1,2,…,n, and the return rate of risky
investment portfolio r(t) satisfies
, where Bi is
i-dimensional standard Brownian Motion, i=1,2,…,n, and the return rate of risky
investment portfolio r(t) satisfies
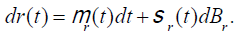 (14)
(14)
Let 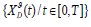 be the wealth process of the insurance company for the
strategy . The insurer uses the self-financing strategy. Based on equations
of (2) and (14), insurer’s wealth follows the equation below:
be the wealth process of the insurance company for the
strategy . The insurer uses the self-financing strategy. Based on equations
of (2) and (14), insurer’s wealth follows the equation below:
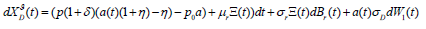 (15)
(15)
With a boundary condition of 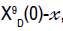 , and
, and
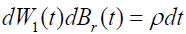 (16)
(16)
where 1 {Br(t), W1(t) / t≥0} are standard Brownian motions on a filtered probability space (Ω,F, {Ft} t≥0, P), Ft is the P-augmentation of the natural filtration, ρ is the coefficient of correlation between Br(t) and W1(t) and ρ≤0; the total amount invested in risky investment, Ξ(t), is a measurable control process adapted to the filtration {Ft}t≥0, satisfying:
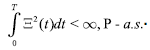 (17)
(17)
Assume that α(t) is a non-negative measurable process adapted to the filtration {Ft}t≤0, satisfying equation (15), that is,
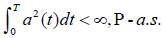 (18)
(18)
And the wealth equation (15) has unique optimal solutions of ((t),a(t),a(t))..
Extension of HJBI equation and solutions of optimal investment and retention of reinsurance
We let Dθ be the set of admissible controls by the market and let π for the
set of admissible strategies ϑ=(Ξ,a,α) of the insurance company. For any
T<∞, a process {θ(t) / t∈[0,T]} satisfies the condition of 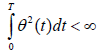 and (t) ≤ 1.
For each θεD, F-adapted process
and (t) ≤ 1.
For each θεD, F-adapted process 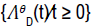 is a real-valued process defined
on (Ω,F, {Ft}t≥0, P) as:
is a real-valued process defined
on (Ω,F, {Ft}t≥0, P) as:
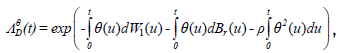 (19)
(19)
By Ito’s differentiation rule, we obtain
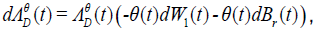 (20)
(20)
Where 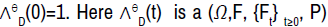 local martingale, and
satisfies
local martingale, and
satisfies 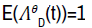 For each θεΘD, a new (real-world) probability measure
Pθ, which is absolutely continuous with respect to P, is defined on (Ω,F(T)) by
For each θεΘD, a new (real-world) probability measure
Pθ, which is absolutely continuous with respect to P, is defined on (Ω,F(T)) by
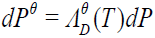 (21)
(21)
The optimal problem of the insurance company can be formulated as a two-player, zero-sum, stochastic differential game as in [7]. The measure θ is the control of one player (the “market”), while the investment portfolio and retention of reinsurance (Ξa,) is the control of player two (the insurer). We define a vector process by:
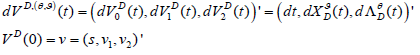 (22)
(22)
The optimization problem is formulated to Min-Max expectation for the utility of the terminal wealth. Given the initial time, t0, the initial wealth of the insurer, X0, the objective function over the class of admissible controls (θ,)ε(Θxπ) is given by
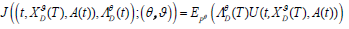 (23)
(23)
In a manner similar to the work in [25] the process A(t) is defined as
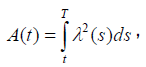
Where  and μr(s) and σr(s). Satisfy equations (10) and (11),
respectively. Therefore μr(t). in stochastic differential equation (15) can be
replaced by λ(t)σr(t). Then performance process is defined to be dependent
on A(t) and
and μr(s) and σr(s). Satisfy equations (10) and (11),
respectively. Therefore μr(t). in stochastic differential equation (15) can be
replaced by λ(t)σr(t). Then performance process is defined to be dependent
on A(t) and 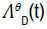 as:
as:
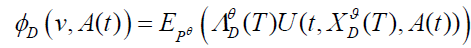
Where 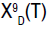 is defined by equation (15) and
is defined by equation (15) and 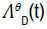 is defined by equation
(19).
is defined by equation
(19).
Since 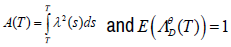 , the utility does not really depend
on A(T), we can transform the utility of state-dependence into the one with
state-independence. Although the utility at terminal time is state-independent,
it is difficult to assure that the performance process defined by equation
(24) satisfies time-consistent condition at the whole state space (Θxπ).
, the utility does not really depend
on A(T), we can transform the utility of state-dependence into the one with
state-independence. Although the utility at terminal time is state-independent,
it is difficult to assure that the performance process defined by equation
(24) satisfies time-consistent condition at the whole state space (Θxπ).
Therefore, the defined form of 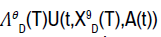 may not be suitable
for dynamic programming. We here assume that our performance process
may not be suitable
for dynamic programming. We here assume that our performance process 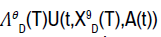 doesn’t satisfy time consistency and the control can be
restricted only to admissible feedback control. Our objective is to min-max
doesn’t satisfy time consistency and the control can be
restricted only to admissible feedback control. Our objective is to min-max 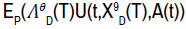 for each (t, v1, v2), which can be proved to be the case
in theorem 1. Our optimal control is not strictly optimal based on the dynamics of the process. However, for any twice continuously differential function
for each (t, v1, v2), which can be proved to be the case
in theorem 1. Our optimal control is not strictly optimal based on the dynamics of the process. However, for any twice continuously differential function 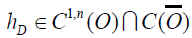 , where
, where 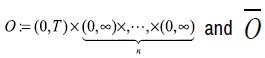 denotes
the closure of O, there exists a partial differential operator
denotes
the closure of O, there exists a partial differential operator 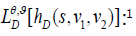
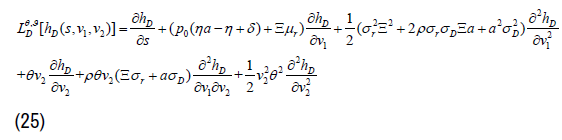
According to Mataramvura and Âksendal (2008) and Bjork T, et al. [15], it is not
Difficult to get the following verification theorem
Theorem 1: Suppose that there exists a function 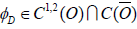 , a
function g(T,t) and an admissible feedback control
, a
function g(T,t) and an admissible feedback control 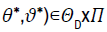 such that
such that
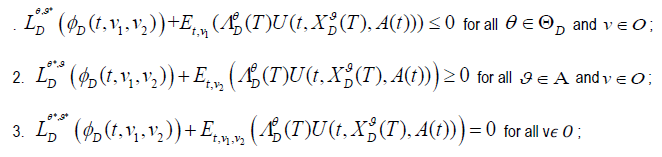
4. The value function is determined by extended HBJI defined by equation (27).
5. since 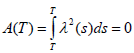 , for all
, for all
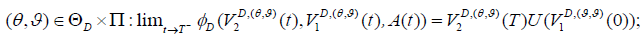
6. Let K denote the set of stopping times τ ≤ T. The family 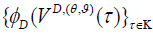 is uniform integral for all
is uniform integral for all 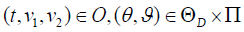
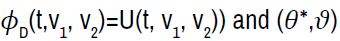 is an optimal control [26,27].
Proof:
is an optimal control [26,27].
Proof:
First, the value function is proved to be determined by extended HBJI
equation as followings. The Ito formula is applied to the performance process 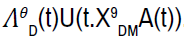 . Expectation of the integration yields:
. Expectation of the integration yields:
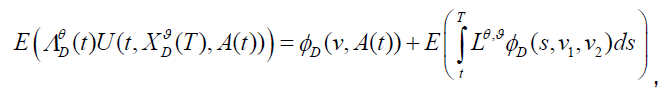
Where the stochastic integral part has vanished because of the integrability Then, 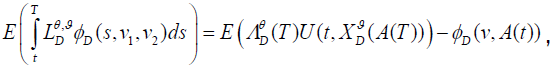
Therefore, we obtain the desired result:
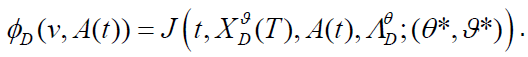
Second (θ*,*) is proved to be the supremum in the value function and is proved to be an admissible feedback control as follows.
Choose (θ,)εΘD xπ, then, for h>0, a randomly chosen initial state (t,v1,v2) and define the control law (θh,ϑh) as
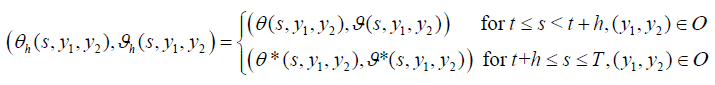
Furthermore, we obtain:
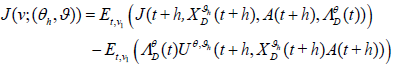
Since 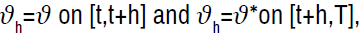 , we have
, we have
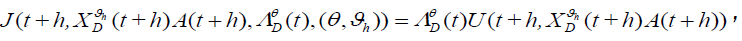
Then we obtain
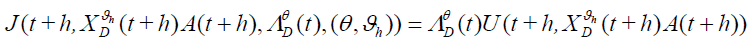
Furthermore, from equation (23) we have 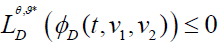 .
.
It gives us that 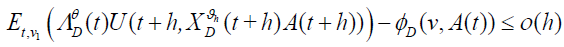 Combining this with expression for
Combining this with expression for 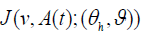 above and the fact that
above and the fact that 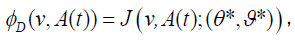
We obtain 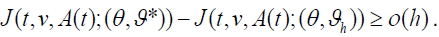
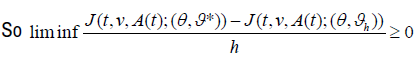
Similarly, we obtain:

Then we have
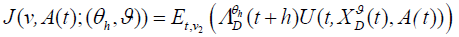
Furthermore, from equation (23) we have 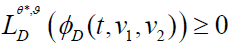 . It gives us that
. It gives us that
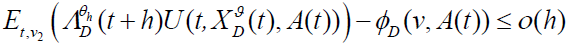
Combining this with expression for 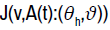 above and the fact that
above and the fact that
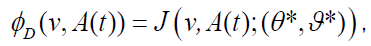
We obtain 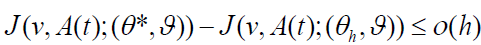 .
.
So 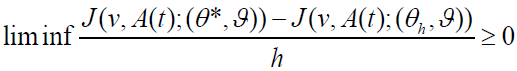
Then, 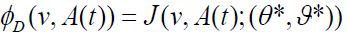 .
.
This finishes the proof.
The optimal investment problem is formulated to Min-Max expectation of the exponential utility of the terminal wealth of an insurance company. Since the utility function is dependent on the present states of v=(t,v1,v2), the condition of HJBI equation is not satisfied. In order to obtain the optimal value function φ*(v,A(t)) and the optimal strategy (θ*,Ξ*,a*θ*), an extended HJBI equation is built as follows which is similar to Bjork T, et al. [7]
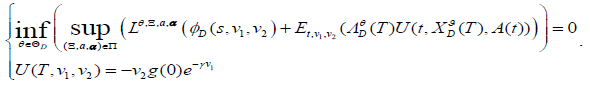 (26)
(26)
A value function of exponential form as in (27) is taken to solve the equation above.
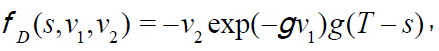 (27)
(27)
Where γ is the coefficient of risk aversion, g(T-s) is an undetermined function with 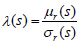 and the boundary condition: g(T-T)=1.
and the boundary condition: g(T-T)=1.
ϑ=(a,θ) and substitution of value function (27) into equation (26) result in the differential operator:
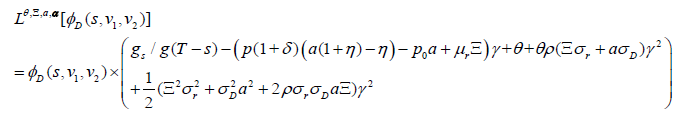 (28)
(28)
We cannot show from equation (27) that
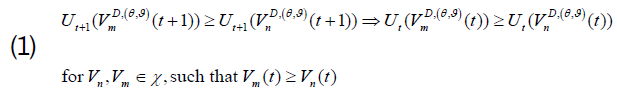
Due to the following facts: from equation (30), we will know that it is not
always the case that 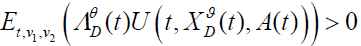
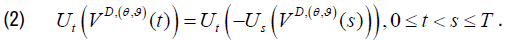
Therefore, we can only construct the extended HJBI equation because acceptable time-consistence cannot be satisfied. Combination of equation (28) and equation (26) leads to extended HJBI equation (29) as following:
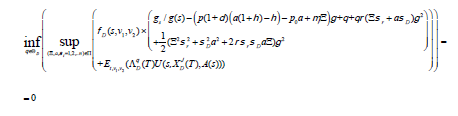 (29)
(29)
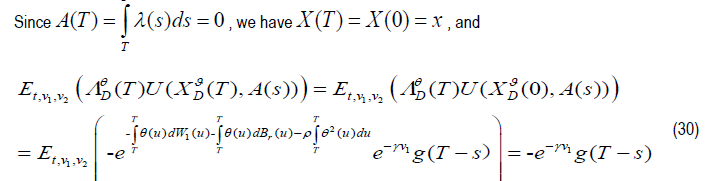
Equations (29) and (30) indicate that φD(s,v1,v2) ≠1 is the sufficient and necessary condition for the existence of optimal solutions [1]. It is necessary to make v1 and v2 different from zero [8]. Maximization over (Ξa,) with fixed
θ∈ΘD leads to the following first order conditions for the maximum point ((θ),a(θ),a(θ)) as equations of (31), (32) and (34), respectively:
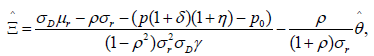 (31)
(31)
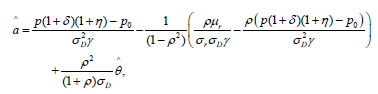 (32)
(32)
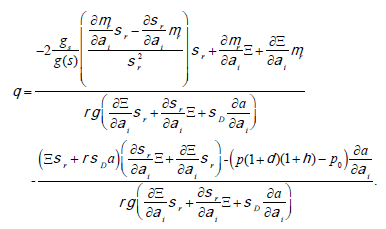 (33)
(33)
Since equation (33) can be written as following simplified form
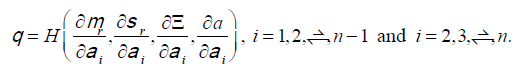
(Please note that the following equal weights is deducted from the non-partially
differential θ related term, θ and other non-partially differential θ related terms
in right hand side of equation (33)) and at the same time, the constraint condition 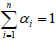 is satisfied as well.
is satisfied as well.
It is implied that only when a1=a2=…,=an-1 and a2=a3=…,=an can the equation (33) hold. Therefore, we have optimal proportions of risky assets invested satisfy:
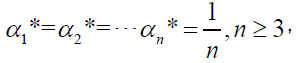 (34)
(34)
That is, optimal proportion of risky assets invested is equally weighted when n≥3.
Putting equation (34) into equations of (10) and (11), respectively, we have
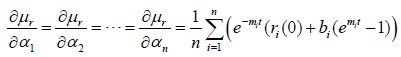 (35)
(35)
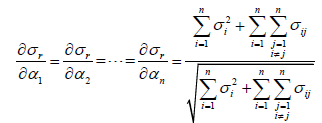 (36)
(36)
Although equally weighted investment strategy is usually thought of as a feasible and convenient investment strategy, it has never been demonstrated theoretically to be an optimal investment strategy under some conditions. Here our theoretical proof has demonstrated the possibility of the equal-weight investment as an optimal strategy. It is especially important to notice that equal weights can simplify greatly the optimization process.
Combination of equations (31) and (32) with equations (29) and (30) and Minimization over θ result in equation (37):
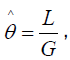 (37)
(37)
where 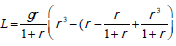 , and
, and
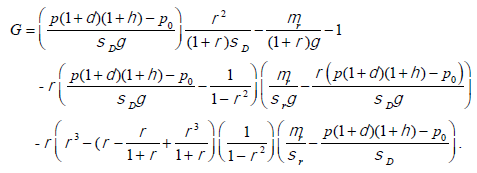
We can easily obtain the optimal solution of (t) by solving equation (37) with the equally weighted investment portfolio. Putting optimal solution of θ into equations (31) and (32), results in the optimal amount invested in risky assets and the optimal
Portion of retention of reinsurance = 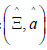 .
.
The optimal wealth process can be expressed as:
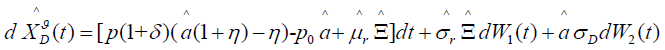 (38)
(38)
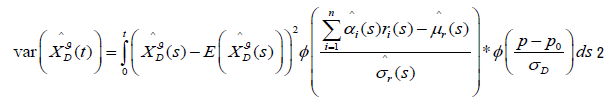 (39)
(39)
Where p is the net premium rate and p0 is the claim loss rate.
The lower control bound with (1-ϖ) confidential level is obtained by combining equations (38) and (39) as following:
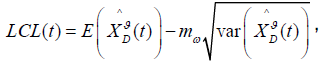 (40)
(40)
Where LCL(t) is lower bound of wealth at time t(t ≤ T, and T is control
period), 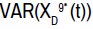 is deviation of optimal wealth, mϖ is the critical value with
1(-ϖ) confidential level, while μr and σr satisfy equations (10), (11) and (34),
respectively.
is deviation of optimal wealth, mϖ is the critical value with
1(-ϖ) confidential level, while μr and σr satisfy equations (10), (11) and (34),
respectively.
Equation (40) is obtained as following by combining equation (31), (32) and (38) with equation (28), using t instead of s and setting it equal to 0:
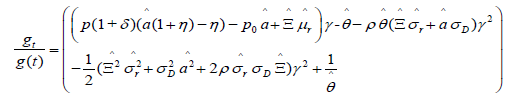 (41)
(41)
where
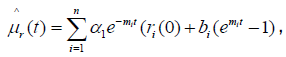 (42)
(42)
and
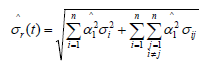 (43)
(43)
Integration of two sides of equation (42) and application of the boundary condition g(T,λT)=1 sult in the formula for g(t):
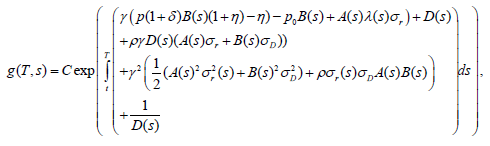 (44)
(44)
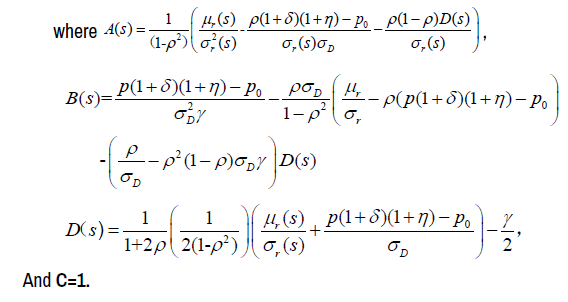
We also analyze the case when â(θ,t)≤0. If â(θ,t)≤0, we should choose â(θ,t)=0 as an optimal strategy. Substitution of â=0 into equation (30) results in equation (48):
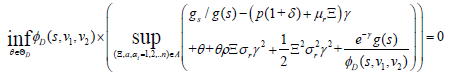 (45)
(45)
Maximization over π with fixed θ∈ΘD leads to the following first order condition for the maximum point (θ).
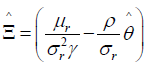 (46)
(46)
With â=0 and in combination of equation (46) with equation (45), minimization over θ results in the first order condition for the minimum point, where: θ=θ.
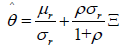 (47)
(47)
Equation (46) and equation (47) lead to equation (48):
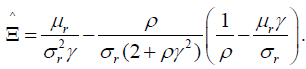 (48)
(48)
Substitution of â =0, equations (47) and (48) into equation (45) with ø(s,v1,v2)≠0 results in equation (49):
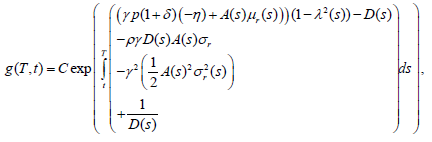 (49)
(49)
where
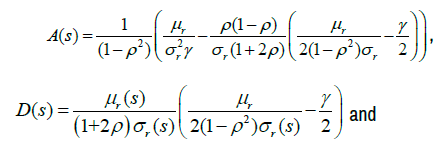
Therefore, analysis above implies the following theorem.
Theorem 2
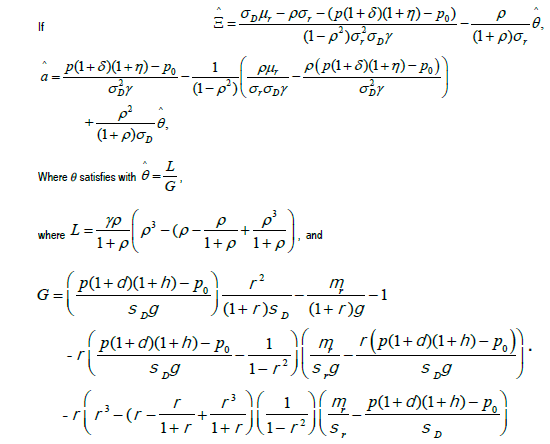
The optimal strategy (θ*,*, θ*)=(θΞ,θ, θ) is given by equations (31), (32), (34) and (37), and the optimal value function is:
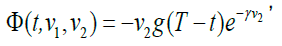 (50)
(50)
Where g(T-t) is given by equation (44).
When a(t)=0, the optimal strategy (θ*,Ξ*, θ*)=(θΞ,θ) is given by equations (47), (48) and (34). The optimal value function satisfies equation (50) where g(T-t) is given by equation (49).
Numerical analysis
The data of annual return rate of S & P 500, Treasury Bonds and Treasury Bills in U.S. from 1965 to 2014 is used in multi-variate Vasicek model. The results are displayed in Table 1. Please note that Table 1 includes the estimated values of three parameters and asymptotic errors of both Vasicek models [28].
| MLE | S&P | Estimation error |
Treasury Bond |
Estimation error |
Treasury Bill |
Estimation error |
|---|---|---|---|---|---|---|
| Estimation(mi) | 4.9677 | 0.2389 | 2.4594 | 0.0654 | 0.1664 | 0.0085 |
| Estimation(bi) | 0.1134 | 0.0240 | 0.0985 | 0.0221 | 0.0509 | 0.0042 |
| Estimation(σi) | 0.5348 | 0.2624 | 0.3473 | 0.0248 | 0.0171 |
For other data, please see Table 2. Table 3 lists optimal solutions of amount invested in risky assets, Ξ*, portion of retention, a1* and proportions of stocks, Treasury Bonds and Treasury Bills a1*, a2* and a3*. Table 3 lists the optimal solutions for different time t. Table 3 indicates that the optimal amount invested in risky assets first decreases and then increases with time, but the optimal portion of retention first increases and then decreases with time. Of course, the optimal solutions can be obtained for other terminal time T. Since insurance business is generally on-going business, which means that the life time is uncertain, it is important to obtain the optimal solutions for varying terminal time. In the following section, sensitivity analyses are carried out to the changes of the important parameters.
| Parameters | Values |
|---|---|
| The coefficient of correlation ρ | -0.2 |
| The average rate of claim loss p0 | 0.15 |
| The volatility of claim loss σD | 0.21 |
| The coefficient of risk aversion у | 2 |
| The net premium rate p | 0.15 |
| The loading of premium δ | 0.05 |
| The cost rate of reinsurance η | 0.1 |
| The initial investment X(0) | 1 |
| The terminal time T | 15 |
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 3.237 | 3.132 | 3.164 | 3.202 | 3.235 | 3.264 | 3.288 | 3.308 | |
| a*= | 0.573 | 0.561 | 0.564 | 0.568 | 0.572 | 0.575 | 0.577 | 0.579 |
| t | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 3.325 | 3.34 | 3.352 | 3.362 | 3.371 | 3.379 | 3.385 |
Varying parameters of σD, η and γ
Figure 1(a) displays the change pattern of time-varying correlation among risky assets invested. Figure 1(b) through (g) shows the change patterns of optimal solutions of the amount invested in risky assets and the optimal portion of the retention for different values of the volatility of claim loss, σD, the rate of (e) indicate that increase in the rate of reinsurance cost will greatly decrease the optimal amount invested in risky assets but greatly increase optimal portion of the retention. Figure 1(f) and Figure 1(g) show that both optimal amount of investment and optimal retention decreases with the increase of risk aversion, which is intuitive (Figures 1a-1g).
Varying parameters of σi and bi,i=1,2,3.
Figures 2(a) through (d) display the change patterns of optimal solutions of the amount invested in risky assets and the optimal portion of the retention with the change of volatilities and the means of long term return of risky assets invested, σi and bi,i=1,2,3. Figures 2(a) and (b) indicate that both optimal reinsurance cost, η, and the coefficient of risk aversion, γ Figure 1(b) and (c) indicate that both the optimal amount invested in risky assets and the optimal portion of the retention decreases with the increase of the volatility of claim loss. The increase of the risk of claim loss tends to make the insurer more willing to increase reinsurance and put less funds in risky assets. Figure 1(d) and amount invested in risky assets and retention portion are greater when the volatility of the return of the stocks, Treasury Bonds and Treasury Bills decrease 10%, respectively; especially they are much more sensitive to the increase in the volatility of the return of stocks and Treasury Bonds than that of Treasury Bills, that is to say, lower volatility of the return of risky assets invested will encourage insurers to put more funds in investment, and more remains for retention of reinsurance. Figures 2(c) and (d) indicate that the optimal amount invested in risky assets increases and the optimal portion of the retention also increases when the means of long term return of the stocks, Treasury Bonds and Treasury Bills increase 10%, respectively; the optimal amount of stocks and Treasury Bonds are much more sensitive to the change of the means of long term return of stocks and Treasury Bonds than to that of Treasury Bills; and the optimal retention is also sensitive to the means of long term returns of all of three kinds of long term risky assets (Figures 2a-2d).
Figure 3(a) through Figure 3(d) display the change patterns of optimal amount investment and optimal retention portions when the correlation coefficient between investment and investment return rate of long term and volatility changes. Figure 3(a) through Figure 3(d) show that the optimal amount of risky investment decreases with the increase of correlation coefficient between investments and claim loss. However, optimal retention portion of reinsurance at first increases with the increase of correlation coefficients and then decreases with the increase of correlation coefficients (Figures 3a-3d).
In this paper, the optimal decision of investment and reinsurance is studied with time-inconsistence under the stochastic differential game framework. Multiple risky assets constitute investment portfolios; the returns of these risky assets follow multi-variate Vasicek model with time-varying correlation; claim losses are correlated with these risky assets. The solution to the extended HJBI equation results in dynamical optimal solutions for the amount invested in risky assets, the optimal portion of the retention and optimal proportions of all risky assets invested. A dynamical optimal bound is built for monitoring and predicting the optimal wealth level. The numerical analyses are carried out under the proposed model. The sensitivity analyses indicate that the optimal amount invested in risky assets in the proposed model are sensitive to most of the parameters except the volatility and the means of the Treasury Bills return at the long-run equilibrium; the optimal portion of the retention is sensitive to all of parameters The volatility and the means of long term returns of all three kinds of risky assets. Our sensitive analysis results are consistent to intuitions, and this demonstrates the effectiveness of our proposed model. Importantly, the investment with equally weighted risky assets can be an optimal strategy. The proposed model can be easily applied in very high dimension investment portfolio.
We calculate the time varying covariance of σij (t) of the return of stocks and bonds. In a manner similar to Korn and Koziol (2006), and Mamon (2004).
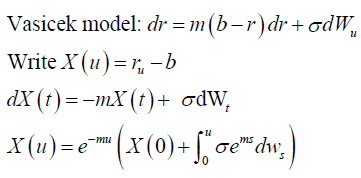
In the following, we calculate the time varying covariance, σij (t), By Itô isometry, we have:
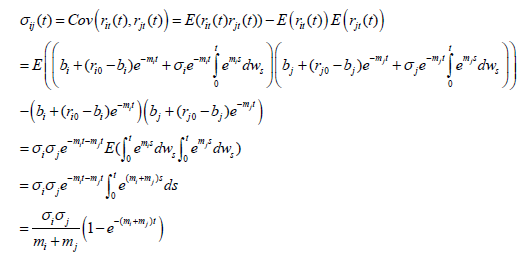
Business and Economics Journal received 6451 citations as per Google Scholar report