Water Loss Dependence on the Change in Permeability Coefficient of the Bottom and the Side Walls of the Channel

Alisher Usmonov^*
*Correspondence: Alisher Usmonov, Tashkent University of Information Technologies, Tashkent, Uzbekistan, Tel: +99871238 6415, Email:

Keywords

Schwartz integral formula • Coefficient of permeability • Zhukovsky function • Hydrodynamic parameter

Introduction

At present in conditions of water scarcity, a mixture of mineralized waters (ground-water, sewage-drainage water, and even sea water) with channel waters are used in irrigation. This is common in the USA, Ukraine, Azerbaijan, Tunisia, Israel, Turkmenistan, and Uzbekistan. In hydrological and water management studies (irrigation, drainage), the determination of the groundwater balance, as well as the general water balance, is still done on the basis of experimental observations of individual elements. The balance is considered as the algebraic sum of water supply and water consumption characterizing the change in water reserves in a given area. The feature of such a hydrological approach to the study of groundwater balance is to find the average values of individual elements for a given area; infiltration of precipitation, irrigation water, evaporation, groundwater inflow and outflow. The homogeneity of the hydrogeological situation is assumed, on which the assumption of the constancy of the values of a number of balance elements over a considerable territory is based. The variety of hydrological and water management conditions requires a large number of experimental observations, which in some cases are not feasible for technical reasons (for example, at deep water bedding), and for the lack of development of a number of issues in the methodology of these observations. The difficulty of setting up experimental studies of infiltration, evaporation, and other balance elements that usually arises in methodological and technical respects, forces the researchers to use the empirical dependencies of these elements on a number of natural factors: aeration zone power, meteorological and other conditions. When experimental definitions of the balance elements are numerically limited, the researchers use an analogy method of similar observations in neighbouring areas. The absence of generally accepted experimental observation techniques in some cases limits their value and gives them the character of subjectivity and even randomness, so, the water balance calculation is often subjective [1-3].

Statement of the problem: Water filtration from a Sprinkler of a furrow-type Irrigation system

Soil is a multiphase and multicomponent medium; it consists of a soil skeleton considered as a solid phase. The soil skeleton has a complex geometry and a large specific surface. It possesses great permeability, i.e. fluid filtration, so, the filtration coefficient greatly depends on the fluid concentration. Consider the problem of water filtering from a sprinkler of a furrow-type irrigation system (Figure 1), here soil capillarity is taken into account. To apply the Zhukovsky jet method to the problem solution, we replace the sprinkler with a source of fluid. In further assumptions, taking one of the lines of equal heads as the cross sections of the sprinkler channel, we extend the results obtained to the case of a sprinkler being the nearest one to the trapezoid of cross section.

The problem of water flow filtration from a channel in a plane statement is considered [4]. Assume that the water flows uniformly along a channel of a trapezoidal cross section BCDC’B’at an average velocity of VT with a flow rate:

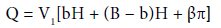
H is the flow depth of the channel defined by equalities and the free surface of the channel, b, B is the width of the channel bottom. Where

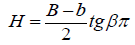
Along the shifted perimeter of DCB, the fluid (water) flows into soil uniformly, and the cross-sectional shape of the prismatic channel consists of an isosceles trapezoid, with an angle of inclination βπ.of the sides to the horizontal plane. Then, the vertical line DE is a symmetrical line of the filtration flow and coincides with the coordinate line oy. Due to the flow mobility along the channel, the fluid penetrates the soil at an angle απ (to the area G_z).

For a reservoir where the fluid (water) is in equilibrium vibration, the angle of penetration is equal to 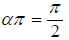(vertically to the walls of the body). Far from the source (at the walls and the bottom of the channel), the depression curve becomes horizontal and this creates the condition to apply the Zhukovsky jet model to the problem under consideration (Figure 2), under the assumption that the backwater curve K₁K is impermeable and horizontal.

The channel is located on the soil surface, which has a permeability coefficient -k. Through the wetted perimeter of the BCDC’B ’ trapezoid, filtration water spreads through the soil, and at depth hF there is an impenetrable confining layer EA. If the permeability coefficient k(x, y) is symmetric with respect to the vertical axis ED (Oy), then AEDCBF (where x>0) is taken as the flow region G_z (z=x+iy); here a free surface AFB is formed, where point F is the point of bending. In the absence of a point of bending, point F coincides with point B.

Along the boundary DE, basically a vertical flow occurs due to the symmetry of the flow region Gz. The Darcy’s law is taken as the law of filtration 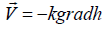[1]:

(1.1)

Where 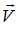-is the filtration rate; h – is the head

Here:

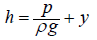(2.1)

Where h is the piezometric height, p, ρ is the pressure and density of fluid particles, y is the ordinate of the point.

Suppose that the flow is a potential, then we can introduce the velocity potential ϕ(x, y) in the form

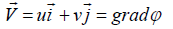
Hence

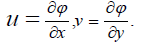(2.2)

Hence we get the equality

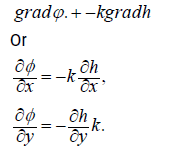(2.3)

If the permeability coefficient k is constant in the flow region, the following potential velocity function is obtained:

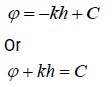
If the fluid is incompressible, then: ρ = const

So, the continuity equation has the following form:

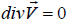
Introduce a flow function ψ(x, y) satisfying the continuity equation

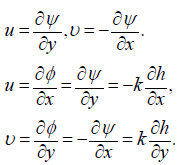(2.4)

Taking into account equalities (2.2) and (2.3), we obtain the following dependence between the functions ϕ(E, C) and ψ = (E, C) introduced for consideration

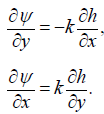(2.5)

If the permeability coefficient k is constant, then the functions ϕ(E, C) ψ = (E, C) and h(x, y) are harmonic in the flow region, and at variable k (x, y) due to the equality:

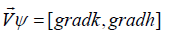
It is obtained that along the line of constant head the permeability coefficient should be constant, i.e.

gradk = gradh,

From here we get the equality

[gradk, gradh]=0.

The problem solution is built by the well-known Zhukovsky method [2]. To do this, introduce the canonical region G0, (the upper half-plane, ς = ξ + iη and η = 0); its real axis coincides with the boundary of the flow region G_z, where (z=x+iy), and introduce the Zhukovsky function

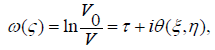
Where V₀−is the filtration rate at some point on the free surface BFA; 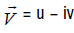iv−is the conjugate complex velocity, 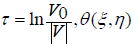-is the angle of inclination of the velocity vector 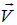to the horizon, i.e. to the axis Ox.

For the introduced function ω(ς), we have the following boundary conditions (Figure 2) [5-7]:

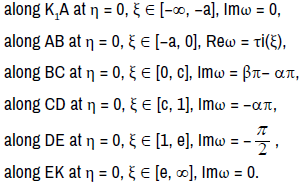
Introducing function 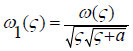and using the Schwartz integral formula (2.4),

we obtain an analytic expression for the Zhukovsky function [8,9]:

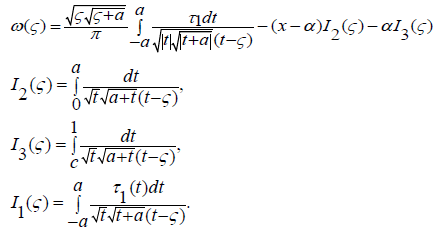(2.6)

To determine the unknown function τ₁(t), using the condition of constant pressure along the free surface AFB, we have equality (1) (in the absence of infiltration and evaporation).

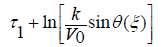(2.7)

Taking into account equalities (2.6) and (2.7), and the Sokhotsky- Plemelj theorem (2.5), we obtain the following singular equation along the free surface AFB:

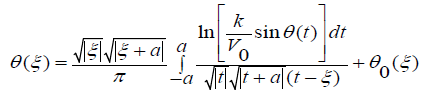(2.8)

Where

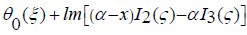
The solution of nonlinear singular integral equation is carried out by the method of successive approximations, where the case of the absence of gravity and surface tension forces θ(0) = θ0(ξ) is taken as zero approximation:

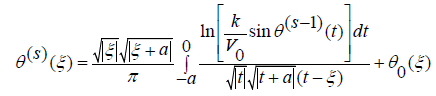(2.9)

Present the problem solution in a linear statement, where it is assumed that the modulus of the filtration rate on the section [a, 0] at η = 0 linearly depends on ξ:

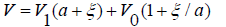(2.10)

Then

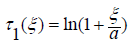
The Zhukovsky function in the region G₀ has the form

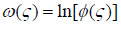(2.11)

Where

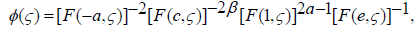(2.12)

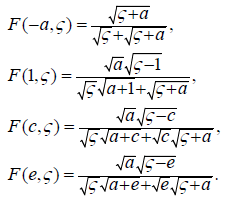
From here we find the expression for the conjugate complex velocity in the region G₀

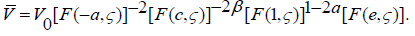(2.31)

Now construct the complex potential function w = ϕ + iψ in the region G₀.

Along BC,DC at

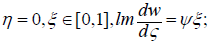
Along KA, BE, DE, and EK at

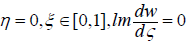
Given these boundary conditions and the Schwartz integral formula, we obtain the integral equality:

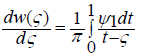(2.14)

Hence, under the condition η = 0, ξ ∈ [0,1] along the permeable boundaries BC and CD, we obtain the equality:

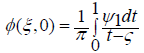(2.15)

Then for an unknown function ψξ we obtain the following singular integral equation:

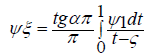(2.16)

By solving equation (2.16) we obtain the function

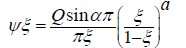(2.17)

Next, from equalities (2.15) and (2.16), we determine the functions w(ξ) and ϕξ:

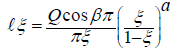(2.18)

The function of complex potential is determined by integration from formula (2.15):

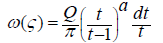(2.19)

Using the expressions for the complex velocity (2.13) and complex potential, we obtain the expression for the function that maps the flow region G_O to the region G₀:

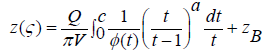(2.20)

Where,

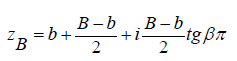
Thus, the solution to the problem is determined by the expressions (2.13), (2.20) obtained in a parametric form:

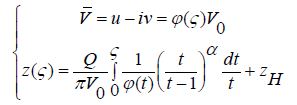(2.21)

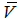Is the velocity of fluid particles, z(ς) is a characteristic function of a moving fluid.

Hydraulic Parameters of Water Moving along the Furrows

Given the boundary conditions and the filtration rate, the following analytical expressions can be obtained to determine the unknown imagery parameters 0, A, 5 and hydraulic parameters (the parameter f is determined from the condition at the point of bending):

The length of the inclined part of the furrow is:

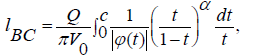(3.1)

Filtered water depth under the furrows is:

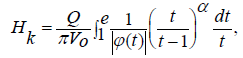
Furrow bottom width is

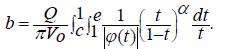(3.2)

The depth of the water flow in the furrow (Figure 1) is determined by the equality of the above formula (3.1):

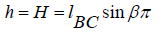
The flow rate of the furrow is determined from the conditions:

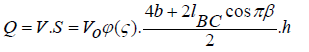
The change in water flow in the furrow is determined from the conditions

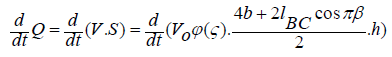
If the point of bending of the depression line is at a point η = 0, ξ = f, then the is met

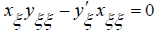
That is ,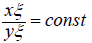

As is known, hence we can write a condition

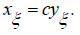
Water flow rate in the furrow flowing through the permeable surface BC is determined by the formula:

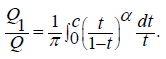(3.3)

Water flow rate in the furrow flowing through the permeable surfaces CD is determined by the formula:

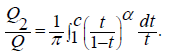
The amount of evaporation from the water surface is determined from the formula:

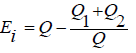
Thus, the dependence of flow rates Q₁ and Q₂ on the parameters of the flow region b, B, h_E, απ and βπ is obtained.

Acknowledgements

Author thanks Grant: QKh-A-QH-2018-291 for financial support.

References

1. Ibad-Zade, Yu. “Water transportation in open channels.” Moscow (1983): 272.
2. Ibad-Zade, Yu. “Distribution patterns of velocities and turbidity in a two-phase open flow.” Technological Progress 10 (1972) 37-39.
3. Ravshanov, Normakhmad, Nozim Kurbonov, and Abduvali Mukhamadiev. "An Approximate Analytical Solution of the Problem of Fluid Filtration in the Multilayer Porous Medium." International Journal of Computational Methods 13 (2016): 1650042.
4. Khujaev, Inkaled, Mamadaliyev Hartdosks, and Aminov Harshfo. "Modelling the propagation of mass consumption waves in the pipeline with damper of pressure disturbances." International Journal of Sciences and Research 74 (2019): 163-170.
5. Vedernikov, Vanardi. “The theory of filtration and its application in the field of irrigation and drainage.” Moscow (1939): 248.
6. Khamidov, Alisher and Khudaykulov SI. Theory of jets of multiphase viscous fluid. Tashkent Fan (2005): 120.
7. Woumeni, Robert, and Michel Vauclin. "A field study of the coupled effects of aquifer stratification, fluid density, and groundwater fluctuations on dispersivity assessments." Advances in Water Resources 29 (2006):1037-1055.
8. Polubarinova-Koch, Pelageia Iakovlevna. Theory of ground-water movement. Princeton University Press (1977).
9. Rehman, Khalil Ur, Abid Ali Khan, MY Malik, and Usman Ali. "Mutual effects of stratification and mixed convection on Williamson fluid flow under stagnation region towards an inclined cylindrical surface." MethodsX 4 (2017): 429-444.